* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download moiré technique
Nonimaging optics wikipedia , lookup
Gaseous detection device wikipedia , lookup
Fourier optics wikipedia , lookup
Reflection high-energy electron diffraction wikipedia , lookup
Thomas Young (scientist) wikipedia , lookup
Photon scanning microscopy wikipedia , lookup
Anti-reflective coating wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Optical aberration wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
Harold Hopkins (physicist) wikipedia , lookup
Optical flat wikipedia , lookup
Retroreflector wikipedia , lookup
Surface plasmon resonance microscopy wikipedia , lookup
Ultraviolet–visible spectroscopy wikipedia , lookup
Astronomical spectroscopy wikipedia , lookup
Interferometry wikipedia , lookup
Diffraction wikipedia , lookup
Shadow play wikipedia , lookup
Phase-contrast X-ray imaging wikipedia , lookup
Fiber Bragg grating wikipedia , lookup
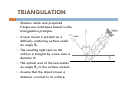
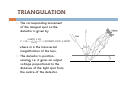
MOIRÉ TECHNIQUE ENGINEERING APPLICATIONS OF LASERS (EAL 604) DR. JALA EL-AZAB MOIRE O TECHNIQUE C QU What is moiré? Moiré techniques Sinusoidal gratings Two angularly displaced gratings Measurement of in-plane deformation and strains Measurement of out-of-plane deformations Sh d moiré Shadow i é and d contour t Vibration analysis Reflection moiré Triangulation p 7,, “Optical p Metrology”, gy , Kjell j J. Gasvik,, John Ref: Chapter Wiley & Sons Ltd, England, 3rd ed. 2002. What is Moiré? The moiré effect can be observed in our everyday surroundings. What is Moiré? The French term “moiré” originates from a type of textile traditionally of silk textile, silk, with a grained or watered pp appearance. Now moiré is generally used for a fringe that is created by superposition of two (or more) patterns such as dot arrays and d grid id lines. li The moiré effect is therefore often ft termed t d mechanical h i l interference. The mathematical description of moiré patterns resulting from the superposition of sinusoidal gratings is the same as for i t f interference patterns tt fformed db by electromagnetic waves. Moiré techniques Moiré can be obtained by the principle of pattern formation of in-plane and out-of plane moirés. I l In-plane moiré: i é measurement off iin-plane l d deformation f i and d strains. O t f l Out-of-plane moiré: i é measurementt off out-of t f plane l deformations (Contouring). SINUSOIDAL GRATINGS Often, gratings applied in moire methods are transparencies with transmittances given by a square-wave function. I Instead d off square-wave ffunctions, i we describe d ib linear li gratings i by sinusoidal transmittances (reflectances) bearing in mind that all types of periodic gratings can be described as a sum of sinusoidal gratings. A sinusoidal grating of constant frequency is given by where p is the grating period and where 0 < a < ½. ½ SINUSOIDAL GRATINGS If the grating is modulated, it will be given by where ψ(x) is the modulation function and is equal to the displacement of the grating lines from its original position di id d b divided by th the grating ti period i d and d u(x) ( ) is i th the displacement. di l t SINUSOIDAL GRATINGS When the two gratings are laid in contact, the resulting transmittance t becomes the product of the individual transmittances represent the original gratings the second grating with doubled frequency depends on the modulation f function i only l THE MOIRÉ N PATTERN SINUSOIDAL GRATINGS Another way of combining gratings is by addition (or subtraction). This is achieved by e.g. imaging the two gratings by double exposure onto the same negative negative. By addition we get The moiré fringes are amplitude modulating The original grating SINUSOIDAL GRATINGS A maximum results in a bright fringe whenever and minima (dark fringes) whenever Both grating t1 and t2 could be phase-modulated by modulation functions ψ1 and ψ 2 respectively. Then ψ(x) has to be replaced by SINUSOIDAL GRATINGS In both multiplication and addition (subtraction), the grating becomes demodulated using Heterodyne technique, thereby getting a term depending solely on ψ(x), (x) describing the moiré fringes. the relations between ψ(x) (and u(x)) and the measuring parameters depend on the different applications. TWO ANGULARLY DISPLACED GRATINGS The mathematical description of this case is the same as for two plane waves interfering under an angle α. Wh two gratings When i off transmittances i t1 and d t2 are llaid id in i contact, the resulting transmittance is not equal to the sum t1 + t2, b butt the th product d t t1 t2. The result is, however, essentially the same, i.e. the gratings form a moiré pattern with interfringe distance This can be applied for measuring α by measurement of d. MEASUREMENT OF IN-PLANE DEFORMATION AND STRAINS T obtain To bt i the th moiré i é pattern, tt one may apply l one off severall methods th d 1. Place the reference grating with transmittance t1 in contact with the model grating with transmittance t2. The resulting intensity distribution then b becomes proportionall to the h product d t1 · t2. 2. Image the reference grating t1 onto the model grating t2. The resulting intensity then becomes proportional to the sum t1 + t2. This can also be done by forming the reference grating by means of interference between two plane coherent waves. 3. Image g the model grating g g t2, and p place the reference g grating g t1 in the image plane. t1 then of course has to be scaled according to the image magnification. The resulting intensity becomes proportional to t1 · t2. 4. Image the reference grating given by t1 onto a photographic film and thereafter image the model grating given by t2 after deformation onto another film. Then the two films are laid in contact. The result is t1 · t2. 5 Do the same as under (4) except that t1 and t2 are imaged onto the same 5. negative by double exposure. The result is t1 + t2. MEASUREMENT OF IN-PLANE DEFORMATION AND STRAINS When multiplying the gratings, the resulting intensity distribution is proportional to t1 · t2 which can be written DC term Modulation function When adding the gratings, the intensity distribution becomes equal to t1 + t2 which can be written DC term Amplitude p modulation of the original reference grating MEASUREMENT OF IN-PLANE DEFORMATION AND STRAINS This distribution has a This corresponds to a displacement equal to The linear and shear strain can be obtained by orienting the model grating and the reference grating along the y-axis, we can in the same manner find the modulation function ψy(y) and the displacement v(y) in the y-direction. MEASUREMENT OF IN-PLANE DEFORMATION AND STRAINS An example of such an intensity distribution with the corresponding displacement and strain MEASUREMENT OF OUT-OF-PLANE DEFORMATIONS IIn-plane l moiré i é pattern tt iis generated t db by superposing i the th reference and object gratings in the same plane. In applying out-of-plane moiré method to the contour mapping, the object grating formed across the object is distorted in accordance with object profile. This out-of-plane moiré method is also termed moiré topography. Th moiré The i é topography t h iis categorized t i d mainly i l iinto t shadow moiré and projection moiré methods. Shadow moiré method is known to be the first example of applying the moiré phenomenon to three-dimensional measurement. SHADOW MOIRE AND CONTOUR SHADOW MOIRE AND CONTOUR The point light source and the detector (the aperture of detector lens is assumed a point) are at a distance l from the reference grating g g surface and their interseparation is s. Period of the reference grating is p (p << l and p << s). Without loss of generality, we may assume that a point O on the object surface is in contact with the grating. ti SHADOW MOIRE AND CONTOUR The grating lying over the object surface is illuminated by the point source and its shadow is projected source, onto the object. The moire pattern observed from the detector is the result of superposition between the grating elements contained in OB of the reference grating and the elements contained i d iin OP off the h objected bj d grating, which is the shadow of elements contained in OA of the reference grating. SHADOW MOIRE AND CONTOUR Assuming that OA and OB have i and j grating elements, respectively, from geometry where n is the order of the moiré pattern hn is the depth of nth-order moiré pattern as measured from the reference grating SHADOW MOIRE AND CONTOUR Since and u(x)= AB A bright fringe is obtained whenever ψ(x) = n, for n = 0,1,2,..., which gives where xP is x component of OP. Substituting above equations in hn and rearranging leads to SHADOW MOIRE AND CONTOUR In the case of plane wave illumination and observation from infinity, α and β will remain constant across the surface and hn describes a contour map with a constant, constant fixed contour interval. interval With the point source and the viewing point at finite distances, α and β will vary across the surface resulting in a contour interval which is dependent on the surface coordinates. This is of course an unsatisfactory condition. SHADOW MOIRE AND CONTOUR However, if the point source and the viewing point are placed at equal heights above the surface and if the surface height variations are negligible compared to l,l then tan α + tanβ will be constant across the surface resulting in a constant contour interval. This is a good solution, solution especially for large surface areas which are impossible to cover with a plane wave because of the limited aperture of the collimating lens. SHADOW MOIRE AND CONTOUR If the surface height variations are large compared to the grating period, diffraction effects will occur, prohibiting a mere shadow of the grating to be cast on the surface. surface Shadow moiré is therefore best suited for rather coarse measurements on large surfaces. surfaces It is relatively simple to apply and the necessary equipment is quite inexpensive. It is a valuable tool in experimental mechanics and for measuring and controlling shapes. SHADOW MOIRE AND CONTOUR As the square wave grating that shadow moiré deals with. In Fourier mathematics, it is known that all types of periodic functions (including square wave function) can be described as a sum of simple sinusoidal functions. In shadow moiré, moiré the amplitude transmittance of the square wave grating is considered as that of a sinusoidal grating. Then the resulting intensity at the point P is proportional to the product TA(xA, y) · TB(xB, y): SHADOW MOIRE AND CONTOUR It is seen that The normalized intensity is given by The last term is solely dependent on height and is the contour term. The other three cosine terms representing the reference grating, although height-dependent, are also dependent on x (location) and, hence, do not represent contours. SHADOW MOIRE AND CONTOUR The patterns corresponding to these three terms can obscure the contours. Intensity distribution along cross-sectional line clearly shows the disturbance of the reference grating itself. To remove these unwanted patterns, Takasaki proposed, to translate the grating in azimuth during exposure. SHADOW MOIRE AND CONTOUR The resultant intensity is proportional to where a ((=K)) is the intensityy bias b (=K/2) is the amplitude φP is the phase related to the temporal phase shift of this cosine variation SHADOW MOIRE AND CONTOUR The unwanted noise patterns are mixed out due to the averaging effect of the reference grating. Vibration Analysis Assume that a point on the surface executes harmonic out-of-plane vibrations given by where z0 is the equilibrium position, a is the amplitude and h frequency. f ω the The intensity distribution of the projected pattern becomes Vibration Analysis The expression can be written as where By photographing this pattern with an exposure ti muchh longer time l than th the th vibration ib ti period i d T , th the resulting transmittance t of the film becomes proportional ti l tto I (x, ( t) averaged d over th the vibration ib ti period. Vibration Analysis This is analogous to time-average holography and gives for the transmittance where J0 is the zeroth-order Bessel function Vibration Analysis The Bessel function amplitude modulates the fringe pattern on the static surface given by z0. Vibration Analysis The light fringes occur when and dark fringes occur when The first dark fringe of this pattern thus corresponds t an amplitude lit d all equall tto to which is a figure representing the sensitivity of the method. REFLECTION MOIRE The reflection moiré method can be applied on the objects with mirror-like surfaces. The smoothness of the surface S makes it possible to image the mirror image of the grating G by means of the lens L. REFLECTION MOIRE A grating can be placed in the image plane of L or the mirror image of G can be photographed before and after the deformation of S. The result is a moiré pattern defining the derivative of the height profile, i.e. the slope of the deformation. TRIANGULATION Shadow Sh d moiré i é and d projected j t d fringes are techniques based on the triangulation principle. A laser beam is incident on a g surface under diffuselyy scattering an angle θ1. The resulting g light g spot p on the surface is imaged by a lens onto a detector D. The optical axis of the lens makes an angle θ2 to the surface normal. Assume that the object moves a distance s normal to its surface. TRIANGULATION The corresponding Th di movementt of the imaged spot on the detector is given by where m is the transversal magnification of the lens. The detector is positionsensing, g, i.e. it g gives v an output p voltage proportional to the distance of the light spot from the centre of the detector. TRIANGULATION It is i th the centroid t id off th the light li ht spott that th t is i sensed d and d thus th the th position measurement is independent of the spot diameter as long as it is inside the detector area. Therefore sharp focusing is not critical. The position of an unexpanded laser beam directly incident on such a detector can be determined to an accuracy of less than 1μm. μ the movement s can be magnified by the lens, thereby increasing the sensitivity. However, the size of the light spot will also be magnified, and this must always lie inside the detector area to avoid measurement errors, thus limiting the usable magnification.