* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Understanding Volatility
Survey
Document related concepts
Transcript
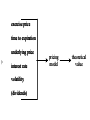
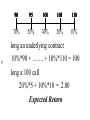
Options Trading Forum October 2nd, 2002 Understanding Volatility Sheldon Natenberg Chicago Trading Co. 440 S. LaSalle St. Chicago, IL 60605 (312) 863-8004 [email protected] exercise price time to expiration underlying price -1- interest rate volatility (dividends) pricing model theoretical value 90 95 100 105 110 20% 10% 20% 20% 40% 20% 10% 20% long an underlying contract -2- 10%*90 + ……. + 10%*110 = 100 long a 100 call 20%*5 + 10%*10 = 2.00 Expected Return -3- The theoretical value is the price you would be willing to pay today in order to just break even. If the expected return of the 100 call is 2.00, what is its theoretical value? interest rates = 12% 2 months to expiration 2.00 - (2.00 x 2%) = 1.96 underlying prices probabilities -4- normal distribution Standard deviation – how fast the curve spreads out. Mean – where the peak of the curve is located -5- All normal distributions are defined by their mean and their standard deviation. 100 + – .25 each day value =.05 -6- + – 2.00 each day value =.75 80 put + – 10.00 each day value = 8.00 90 days to expiration 120 call option value +1 S.D. ˜ 34% -1 S.D. ˜ 34% ±1 S.D. ˜ 68% (2/3) mean ±2 S.D. ˜ 95% (19/20) +2 S.D. ˜ 47.5% -2 S.D. ˜ 47.5% -7- -1 S.D. +1 S.D. -2 S.D. +2 S.D. Mean – the break even price at expiration for a trade made at today’s price (forward price) -8- Standard deviation – volatility Volatility: one standard deviation, in percent, over a one year period. -9- 1-year forward price = 100.00 volatility = 20% One year from now: • 2/3 chance the contract will be between 80 and 120 (100 ± 20%) • 19/20 chance the contract will be between 60 to 140 (100 ± 2 x 20%) • 1/20 chance the contract will be less than 60 or more than 140 What does an annual volatility tell us about movement over some other time period? -10- monthly price movement? weeky price movement? daily price movement? volatilityt = volatilityannual x v t Daily volatility (standard deviation) Trading days in a year? 250 – 260 -11- Assume 256 trading days t = 1/256 v t = v 1/256 = 1/16 volatilitydaily ˜ volatilityannual / 16 volatilitydaily = 20% / 16 = 1¼% One trading day from now: -12- • 2/3 chance the contract will be between 98.75 and 101.25 (100 ± 1¼%) • 19/20 chance the contract will be between 97.50 and 102.50 (100 ± 2 x 1¼%) Weekly volatility: t = 1/52 v t = v 1/52 ˜ 1/7.2 volatilityweekly = volatilityannual / 7.2 -13- Monthly volatility: t = 1/12 v t = v 1/12 ˜ 1/3.5 volatilitymonthly = volatilityannual / 3.5 stock = 68.50; volatility = 42.0% -14- daily standard deviation? ˜ 68.50 x 42% / 16 = 68.50 x 2.625% ˜ 1.80 weekly standard deviation? ˜ 68.50 x 42% / 7.2 = 68.50 x 5.83% ˜ 4.00 stock = 68.50; volatility = 42.0% daily standard deviation = 1.80 +.70 +1.25 -.95 -1.60 +.35 -15- Is 42% a reasonable volatility estimate? How often do you expect to see an occurrence greater than one standard deviation? 8 – normal distribution 0 8 + lognormal distribution -16- -17- underlying price = 100 normal lognormal distribution distribution 3.00 3.00 110 call 90 put 3.00 2.50 110 call = 2.75 90 put = 3.00 Are the options mispriced? Could there is something wrong with the model? future volatility: The volatility of the underlying contract over some period in the future -18- historical volatility: The volatility of the underlying contract over some period in the past forecast volatility: Someone’s estimate of future volatility implied volatility: -19- derived from the prices of options in the marketplace the marketplace’s forecast of future volatility implied volatility exercise price time to expiration -20- pricing model underlying price interest rate volatility 3.25 31% ??? theoretical value 2.50 27% Option trading decisions often begin by comparing -21- implied volatility = price to future volatility = value historical volatility forecast volatility Volatility Trading Initially buy underpriced options or strategies, or sell overpriced options or strategies Offset the option position by taking an opposing market position, delta neutral, in the underlying contract -22- Periodically buy or sell an appropriate amount of the underlying contract to remain delta neutral over the life of the strategy (dynamic hedging) At expiration liquidate the entire position In theory, when the position is closed out the total profit (or loss) should be approximately equal to the amount by which the options were originally mispriced. Volatility Trading Risks -23- You may have incorrectly estimated the future volatility The model may be wrong SPX Historical Volatility January 1990 - August 2002 35% 50-day volatility 250-day volatility 30% 25% -24- 20% 15% 10% 5% Jan-90 Jan-91 Jan-92 Jan-93 Jan-94 Jan-95 Jan-96 Jan-97 Jan-98 Jan-99 Jan-00 Jan-01 Jan-02 Volatility characteristics -25- serial correlation – in the absence of other data, the best volatility guess over the next time period is the volatility which occurred over the previous time period. mean reversion – volatility tends to return to its historical average momentum – a trend in volatility is likely to continue Volatility Cones 40 38 36 -26- implied volatility (%) 34 32 30 28 26 24 22 20 0 3 6 9 12 15 18 21 time to expiration (months) 24 27 30 33 36 Volatility Forecasting Methods -27- (G)ARCH – (generalized) autoregressive conditional heteroscedasticity (V)ARIMA– (vector) autoregressive integrated moving average SPX Daily Price Changes: January 1990 - August 2002 250 225 200 175 number of days: 3186 biggest up move: +5.73% (24 July 2002) biggest down move: -6.87% (27 October 1997) mean: +.0364% standard deviation: 1.0217% volatility: 16.24% skewness: -.0263 kurtosis: +3.9072 -28- number of occurrences 150 125 100 75 50 25 0 -7% -6% -5% -4% -3% -2% -1% 0% daily price change (nearest 1/8 percent) 1% 2% 3% 4% 5% Volatility Skew: The tendency of options at different exercise prices to trade at different implied volatilities -29- A consequence of how people use options weaknesses in the pricing model SPX June Implied Volatilities - 22 February 2002 38 36 34 32 30 28 -30- 26 24 22 20 18 16 14 750 800 850 900 950 1000 1050 1100 1150 1200 1250 1300 1350 1400