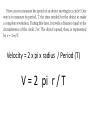Download Equilibrium and the Equilibrant

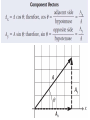
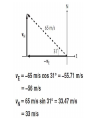
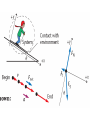
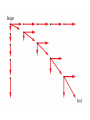
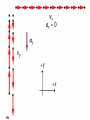
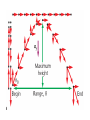
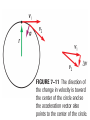
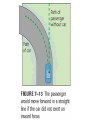
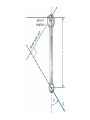
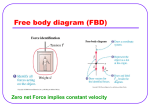
Equilibrium and the Equilibrant
An object is in equilibrium when the net force on it
is zero.
When in equilibrium, an object is motionless or
moves with constant velocity.
Equilibrium and the Equilibrant
An object is in equilibrium when the net force on it
is zero.
When in equilibrium, an object is motionless or
moves with constant velocity.
The Equilibrant is the equal and opposite force that
makes the net force = zero.
Suppose two forces are exerted on an object and the
sum is not zero.
How could you find a third force that, when added to the
other two, would add up to zero?
Such a force, one that produces equilibrium, is
called the equilibrant.
How could you find a third
force that, when added to
the other two, would add up
to zero?
Such a force, one that
produces equilibrium, is
called the equilibrant.
To find the equilibrant, first
find the sum of the two
forces exerted on the
object. This sum is the
resultant force, R.
Such a force, one that
produces equilibrium, is
called the equilibrant.
Adding the EQUILIBRANT to the other vectors
now makes the net force = 0 All of the forces
are in EQUILIBRIUM.
Components
A coordinate system allows
you to expand your
description of a vector.
Vector A is broken up or
resolved into two component
vectors.
Ax , is parallel to the x-axis,
and the other, Ay , is parallel
to the y-axis.
The original vector is the sum
of the two component vectors.
A = Ax + Ay
The original
vector is the
sum of the two
component
vectors.
A = Ax + Ay
The process of breaking a vector into its components is
sometimes called vector resolution.
The magnitude and sign
of component vectors
are called the
components.
An airplane flies at 65 m/s in the direction 149°
counterclockwise from east. What are the east and
north components of the plane’s velocity?
Motion in two dimensions can be solved by breaking
the problem into two interconnected
one-dimensional problems.
For instance, projectile motion can be divided into a
vertical motion problem and a horizontal motion
problem.
The vertical motion of a projectile is exactly that of
an object dropped or thrown straight up or down. A
gravitational force acts on the object accelerating it
by an amount -g.
VELOCITY = ACCELERATION x TIME
V = -g * t
V = -9.8 x t
DISPLACEMENT =
d = v0t + 1/2at2
Analyzing the horizontal motion of a projectile is the
same as solving a constant velocity problem. A
projectile has no thrust force and air drag is
neglected, consequently there are no forces acting in
the horizontal direction and thus, no acceleration,
a=0
VELOCITY = CHANGE IN DISPLACEMENT /
CHANGE IN TIME
V=d/T
DISPLACEMENT = VELOCITY x TIME
d=V/T
Vertical motion and horizontal motion are connected
through the variable time.
The time from the launch of the projectile to the
time it hits the target is the same for vertical motion
and for horizontal motion.
Therefore, solving for time in one of the dimensions,
vertical or horizontal, automatically gives you the
time for the other dimension.
THE TIME IT TAKES FOR THE OBJECT TO FALL
STRAIGHT DOWN AND HIT THE GROUND IS
EXACTLY THE SAME TIME IT TAKES FOR THE
PROJECTILE TO FALL UNTIL IT HITS THE GROUND.
Remember – when we shot the marble out
horizontal and dropped the other ball, the both
hit the floor at the same time.
If we know the time for the vertical motion, we
will know the time for the horizontal motion.
WE WILL USE THE EQUATION FOR
DISPLACEMENT IN THE Y – DIRECTION TO FIND
THE TIME IT TAKES TO FALL TO THE GROUND.
d = v0t +
2
1/2at
ONCE WE KNOW THIS TIME, WE CAN USE THE
TIME TO SOLVE FOR VELOCITY AND
DISPLACEMENT IN THE X – DIRECTION
( V = D / T ) OR ( D = V x T )
Velocity = 2 x pi x radius / Period (T)
V = 2 pi r / T
FORCE DUE TO CENTRIPETAL ACCELERATION – THE FORCE
OF GRAVITY OF SUN OR TENSION IN STRING SWINGING
BALL AROUND OR FRICTION FORCE HOLDING CAR GOING
AROUND CURVE ON ROAD