Download Chapter 2 CELESTIAL COORDINATE SYSTEMS

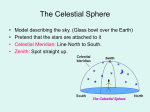
Chapter 2
CELESTIAL COORDINATE SYSTEMS
2-A. Introduction
There are several different ways of representing the appearance of the sky or describing the
locations of objects that we see in the sky. One way is to imagine that every object in the sky is
located on a very large and distant sphere called the celestial sphere. This imaginary sphere has
its center at the center of the Earth. Since the radius of the Earth is very small compared to the
radius of the celestial sphere, we can imagine that this sphere is also centered on any person or
observer standing on the Earth's surface. Every celestial object (e.g., a star or planet) has a definite
location in the sky with respect to some arbitrary reference point. Once defined, such a reference
point can be used as the origin of a celestial coordinate system. Now, there is an astronomically
important point in the sky called the vernal equinox, which astronomers use as the origin of such a
celestial coordinate system. The meaning and significance of the vernal equinox will be discussed
later.
In an analogous way, we represent the surface of the Earth by a globe or sphere. Locations on
the geographic sphere are specified by the coordinates called geographic longitude and latitude.
The origin for this geographic coordinate system is the point where the Prime Meridian and the
Geographic Equator intersect. This is a point located off the coast of west-central Africa. To specify
a location on a sphere, the coordinates must be angles, since a sphere has a curved surface.
Hence, longitude and latitude are angular distances from the origin described above. Longitude is
measured west or east from the origin (or prime meridian), and latitude is measured north or south
from the origin (or geographic equator). If a ship happens to be located exactly at the geographic
origin, we would say it has a longitude of 0 degrees (also written 0o) and latitude of 0o.
When one uses the celestial sphere to represent the sky, any measurements of position must
also be angles. As on a geographic globe, two such angles are necessary to uniquely specify the
location of any object on the celestial sphere. The two angles or coordinates that astronomers use
to specify position with respect to the vernal equinox are called right ascension and declination.
A peculiar thing about right ascension is that, though it is an angle, it is usually expressed in
time units, that is, hours, minutes and seconds of time.
This is because there is a definite
relationship between right ascension and something called sidereal time (sidereal time will be
defined and studied later). An analogous relationship exists between longitude and time. A star
located exactly at the vernal equinox would have a right ascension of 0 hours, 0 minutes (other ways
of designating this are 0h 00m or 0:00) and a declination of 0 degrees, 0 arcminutes (0o 00' or 0:00).
Note: Do not confuse minutes of time with arcminutes, they are not the same.
2-B.
See section
2-B. Angular or Arc Measurement.
Any circle can be divided into any number of equal parts. For example, imagine dividing a circle
into 4 equal parts. Any of these parts is called an arc and would be a certain fraction of the
circumference of the circle; in this case, one fourth of a circumference. The ancient Babylonians
found it convenient to divide a circle into 360 equal parts, which we call degrees. Thus,
One degree is 1/360th of a circle's circumference.
The Babylonians had an apparent fixation on multiples of 60, so they further divided each degree
into 60 equal parts called arcminutes, or minutes of arc. That is,
1 arcminute (1’) is 1/60th of a degree.
To allow for greater precision, they decided to divide each arcminute into 60 equal parts called
arcseconds, or seconds of arc. Hence,
1 arcsecond is 1/60th of an arcminute or 1/3600th of a degree.
Such a system of measurement, based on the number 60, is called a sexagesimal system. We find
a sexagesimal system far more difficult to use than a decimal system, but such a system did not
daunt the Babylonians or the Egyptians and Greeks who also adopted this system. Unfortunately, it
became so ingrained in early western civilization that it is still in common use for making angular
measurements today. Thus we must learn to work with it. You should note that we also use a
sexagesimal system for counting time. Often, we shall also want to express angular distance in
decimal degrees. That is, 50 15’ in the sexagesimal system is equivalent to 5.25 degrees in the
decimal system.
Remember that astronomers find it useful to express the celestial coordinate, right ascension, in
time units. This is because the Earth rotates eastward on its axis, once every day. This makes the
celestial sphere appear to turn at the same rate, but in the opposite direction, namely, westward.
That is, if one faces south, stars would appear to move from the east towards the west, which would
be from your left to your right and is referred to as the apparent diurnal rotation of the celestial
sphere.
The rate of this motion is 15 degrees per hour. This number comes from the fact that Earth, or
celestial sphere (you may assume one or the other rotates but not both), makes one complete turn
through 360 degrees in 24 hours. This also means that the Earth rotates through an angle of 1
degree every four minutes of time. Since 1 degree contains 60', then the Earth turns 15' every 1m.
This should point out the distinct difference between arcminutes and time minutes. One is an angle
and the other is a time. Never substitute one unit's abbreviation for the other, that is, never
write 45' (forty-five arcminutes) when you mean 45m (forty-five minutes of time), or vice
versa.
2-C. The Equatorial Coordinate System
The diagram below is a schematic of the celestial sphere. The axis of rotation of the Earth or
the Celestial sphere, depending on which you assume is rotating, is labeled. The two points where
the axis touches the celestial sphere are called the north and south celestial poles, NCP and
SCP.
Midway between the poles is a great circle that divides the celestial sphere into two
hemispheres. This circle is called the celestial equator (CE).
Celestial Equator: The great circle on the celestial sphere, every point of which is exactly
90 degrees from the celestial poles.
There is a family of great circles that run from one celestial pole to the other and cross the
celestial equator at a right angle. These are called hour circles of right ascension and they are
analogous to meridians of longitude on the Earth
Remember that a point called the vernal equinox (VE) is the origin of our celestial coordinate
system. This point is located on the celestial equator. Right ascension starts at the vernal equinox
and increases eastward from there, all the way around the celestial sphere back to the vernal
equinox again. That is, RA increases eastward from 0 to 24 hours. On a globe or star chart, the
number zero marks the hour circle passing through the vernal equinox. This hour circle is called the
equinoctial colure (EC).
There is another family of circles, each member of which runs around the celestial sphere
parallel to the celestial equator, anywhere between the latter and the celestial poles. These are
called parallels of declination and are analogous to parallels of latitude on the Earth. All of these
circles are smaller than the celestial equator and the closer one is to the celestial poles, the smaller
it is. The celestial equator is itself a parallel of declination. On a globe or star chart, there should be
a number written somewhere on each of these circles to identify what declination that circle
represents.
Declination is an angle measured north or south from the celestial equator. This angle can be
imagined as an arc drawn on a globe starting at the celestial equator and extending along an hour
circle to the parallel of declination passing through the object we are trying to locate. Note and
memorize the following:
Right ascension (α) is the angular distance measured eastward around the sky from the vernal
equinox.
Declination (δ) is the angular distance measured north (+) or south (-) from the celestial
equator.
All objects located on the same parallel of declination have the same declination but
different right ascensions. Similarly, all objects located on the same hour circle have the
same right ascension but different declinations.
2-D. Locating Objects on a Celestial Globe or Star Chart by Interpolation
The star chart below is an attempt to represent a portion of the celestial sphere in such a way
so as to account for its curvature. This kind of map or chart is referred to as an orthrographic
projection. In the chart, there is an hour circle of right ascension drawn every hour for a limited
portion of the sky centered on the equinoctial colure. The right ascension for each hour circle is
labeled along the bottom of the chart and parallels of declination for every 10 degrees are labeled
along the right edge of the chart.
In order to locate an object on the celestial sphere, remember the following rule:
Through any object on the celestial sphere, one can draw a definite hour circle of right
ascension and a definite parallel of declination.
That is, the hour circles and
declination parallels that are
already drawn on a globe or
star chart are referred to as
fiducial ones, but they are
not the only ones that could
be drawn.
Hence, if the
parallel of declination passing
through an object is not
exactly one of the fiducial
values, you will need to
employ a technique called
interpolation to determine
the value of that object's
declination, .
For example, if an object
has a declination of 17o 30',
and the fiducial parallels of
declination are drawn every
10o apart, you will need to
know what fraction of the
distance between the 10th
and
20th
parallels
corresponds
to
this
declination.
The fractional
distance from the 10th parallel
towards the 20th parallel
would be (17.50-10.00)/(20.010.0) or 7.50/10.00=0.75, that
is, 3/4ths the distance.
Notice
that
we
have
converted the sexagesimal
value of 17o 30' to its decimal
equivalent, 17.50 degrees,
with
2
decimal
place
precision, for convenience in using a calculator.
Similarly, if a star has RA=2h 20m, its hour circle is on third of the distance from the 2nd hour
circle to the 3rd hour circle. This is because 20m is 1/3rd (or 0.33) of an hour.
2-E. The Celestial Horizon System
When we stand at most locations on the Earth, we have the distinct impression that the Earth
is flat. This occurs because the curvature of the small area of the Earth usually visible is very slight.
We call this “flat Earth” the Plane of the Horizon and divide it up into 4 quadrants, each containing
90o, by using the cardinal points of the compass. The latter are the North, South, East, and west
points of the horizon. We describe things as being vertical or “straight up” if they line up with the
direction of gravity at that location. It is easy for us to determine “straight up” because we have a
built in mechanism for this in the inner ear (the semicircular canals). Because it seems so “natural”,
we build a coordinate system on these ideas called the Horizon System.
The Celestial Horizon System is another coordinate systems that astronomers find useful for
locating objects in the sky. It is depicted in the Figure below.
Figure 1. The above diagram is a skewed perspective, schematic diagram of the
celestial sphere with circles drawn only for the half above the horizon. Circles on
the far side, or western half, of the celestial sphere are drawn as dashed curves.
All the reference circles of this system do not share in the rotation of the celestial sphere and,
therefore, this coordinate system is fixed with respect to a given observer. The basis for the system
is the direction of gravity. We can describe this as the line from the observer on the surface of the
Earth through the center of the Earth. When this line is extended out to the celestial sphere, it
intersects the sky in two opposite points called the ZENITH and the NADIR. For any observer, the
zenith is the point in the sky directly overhead. (The point on the celestial sphere that is overhead or
at the zenith for you is not the same point on the celestial sphere that is overhead for someone at a
different location.) The great circle halfway between the zenith and the nadir is called the Celestial
Horizon, Astronomical Horizon, or True Horizon and it is the fundamental reference circle for this
coordinate system. (Do not confuse the astronomical horizon with the Visible Horizon, the place
where the earth and sky seem to meet.) See Figure 1, which shows circles drawn for only the half of
the celestial sphere that is above the horizon, except for the LCM.
The Earth is extremely small compared to the size of the celestial sphere, therefore, the Earth
and any observer on the Earth are to be imagined as a point at the center of the sphere. The
celestial horizon is different for different observers. That is, the celestial horizon will divide the sky
into different halves, depending on your geographic location on the Earth.
Now imagine a family of great circles drawn on the celestial sphere in such a way that each
circle of the family passes through the zenith and nadir and crosses the horizon at a right angle.
These circles are called Vertical Circles. You should be able to identify these circles in the above
diagram.
The vertical circle that passes through the east point of the horizon, the zenith, and the west
point of the horizon is called the Prime Vertical.
The vertical circle that connects the north point of the horizon, the zenith, and the south
point of the horizon is very special and is known as the Local Celestial Meridian (LCM).
In the diagram, the LCM is the only vertical circle that lies in the plane of the paper. The Local
Celestial Meridian is a reference circle that is used for measuring local time and will be referred to
frequently in future exercises.
The half of the local celestial meridian (LCM) from the north celestial pole (NCP), through the
zenith, to the south celestial pole (SCP) is called the upper meridian and the other half is the lower
meridian. Notice that a part of the upper meridian can be below the horizon and part of the lower
meridian can be above the horizon, depending on one's latitude.
Almucantars and vertical circles form a grid of intersecting circles on the celestial sphere for the
celestial horizon system. This grid is analogous to that formed by the parallels of latitude and
meridians of longitude on the surface of the Earth.
The first coordinate of the horizon system (analogous to latitude on the Earth) is called
ALTITUDE. It is the angular distance of a point from the horizon. The altitude is 0o 00’ for an
object that is located on the horizon and increases upwards towards the zenith. The altitude at the
zenith is exactly 90o. Negative values for altitude mean an object is below the horizon. All objects
with the same altitude lie along a circle parallel to the horizon. Such a circle is often called a
parallel of altitude or an almucantar and they are labeled such in the above diagram.
The other angle of the celestial horizon system is called AZIMUTH. This is an angle that is
measured around the celestial sphere, starting at the vertical circle passing through the north
point. The value of the angle increases from 0o anywhere along this vertical circle, eastward. At the
east point the azimuth is 90o. The azimuth at the south point is 180o and it is 270o at the west point.
Refer to the above diagram. The point where any vertical circle crosses the horizon has a definite
azimuth, that is, it is located at a definite angular distance from the North Point of the horizon.
2-F. Orientation of the Equatorial System within the Horizon System
Figure 2 below depicts the Earth with its axis of rotation shown vertical and its geographic
equator shown lying in a horizontal plane that is perpendicular to the axis. If an observer is located
at point A, their latitude is indicated by the angle phi (). A line drawn from the center of the Earth,
through the observer at A, and then continued upwards towards the celestial sphere, points to the
observer’s zenith, which is labeled ZA in the figure. A similar line is drawn for an observer standing
at point B, with latitude beta (), pointing to their zenith which is labeled ZB and for an observer at C,
with latitude gamma (), whose zenith is labeled ZC. It should be clear that the zenith is located at a
different point on the celestial sphere for different observers. Additionally, the horizon for each of
these observers intersects the celestial sphere in a different way so that what is above or below their
horizon will be different.
A line through A, tangent to the Earth lies in the plane of the observer’s horizon and indicates
the directions to the north and south points (labeled NPH & SPH in the figure) of the horizon. Similar
remarks are true for the hypothetical observers at B and C. Clearly, the half of the sky that is above
an observer's celestial horizon is different for different observers.
Fig, 2. A schematic diagram showing how the location of an
observer’s zenith and nader in their sky depends on latitude.
Figure 3 depicts the Earth with the shaded plane of the geographic equator drawn midway
between the north geographic pole and the south geographic pole (labeled NGP & SGP). The line
Figure 3. A schematic diagram showing why the altitude of
the NCP for an observer is equal to the observer's latitude.
drawn connecting the geographical poles is the axis of rotation of the Earth. A celestial hemisphere,
reduced in size to fit in the diagram, is drawn centered on an observer who is located somewhere
near mid-latitude in the Northern Hemisphere. A line is drawn through the observer parallel to the
Earth’s axis of rotation. Since parallel lines may be considered to indicate the same point on the
celestial sphere, both of these lines indicate the direction of the north celestial pole (labeled NCP in
the figure). Although the NCP is shown in the figure to be two separate points, they are actually the
same place in the sky as seen by the observer. Similar geometric remarks may be applied to show
that the plane of geographic equator and the plane of the celestial equator, as labeled in the
diagram, lie in the same plane as seen by the observer.
By definition, the angle between the observer and the geographic equator is the observer's
latitude, labeled as . The point on the celestial sphere over the observer's head is the zenith (Z),
and the point under foot on the other side of the celestial sphere is the nadir.
Using some plane geometry, it is easy to show that the observer would see the north celestial
pole (NCP) located at an angle above the North Point of the horizon equal to the observers latitude
(). This geometric argument is shown in the lower right of Fig. 3.
Now imagine yourself in Figure 2, standing at the north geographic pole (latitude 90o N.). The
north celestial pole (NCP) would have an altitude of 90o and, therefore, be at your zenith. The
celestial equator and celestial horizon would coincide.
Now picture yourself on the Earth's equator, at 0o latitude. Here the celestial equator would pass
through your zenith and the north celestial pole (NCP) would lie at the North Point of the horizon and
have an altitude of 0o. Hence, the following general rule:
THE ALTITUDE OF THE NORTH CELESTIAL POLE IN DEGREES IS ALWAYS NUMERICALLY
EQUAL TO THE LATITUDE OF THE OBSERVER.
Also, for any observer located in the northern hemisphere of the Earth, the north celestial pole
(NCP) is always a point located on the local celestial meridian, between the zenith and the north
point of the horizon. Since the LCM is also the vertical circle connecting the zenith and the north
point of the horizon, and azimuth is measured from the latter point eastward, the azimuth of the
north celestial pole (NCP) is always equal to 0o.
Furthermore, from Fig. 2 the following geometric relationship may be deduced:
THE CELESTIAL EQUATOR INTERSECTS THE LOCAL CELESTIAL MERIDIAN AT ANGLE
BELOW THE ZENITH NUMERICALLY EQUAL TO THE LATITUDE.
This is a corollary to the previous general rule about the altitude of the north celestial pole.
2-G. Other Astronomical Coordinate Systems
Two other commonly used coordinate systems used in astronomy are :
1. Ecliptic coordinates
2. Galactic coordinates.
The ecliptic is the circle in the sky that results from projecting the Earth’s orbit onto the celestial
sphere. The ecliptic is the fundamental circle of the ecliptic coordinate system. Latitude is the
angular distance of an object north or south from the ecliptic and longitude is measured from the
vernal equinox, eastward along the ecliptic. This system is used from computing the positions of the
planets.
The fundamental circle of the galactic coordinate system is based on what is believed to be the
central plane of the disk of the Milky Way Galaxy and is called the galactic equator. Galactic latitude
is the angular distance north or south of this circle and galactic longitude is measured along the
galactic equator eastward from what is believed to be the center of the galaxy .