* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download force
Coriolis force wikipedia , lookup
Center of mass wikipedia , lookup
Equations of motion wikipedia , lookup
Seismometer wikipedia , lookup
Electromagnetism wikipedia , lookup
Fictitious force wikipedia , lookup
Classical mechanics wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Centrifugal force wikipedia , lookup
Fundamental interaction wikipedia , lookup
Classical central-force problem wikipedia , lookup
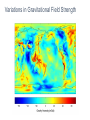
SP1. Students will analyze the relationships between force, mass, gravity, and the motion of objects. d. Measure and calculate the magnitude of frictional forces and Newton’s three Laws of Motion. e. Measure and calculate the magnitude of gravitational forces. g. Measure and calculate centripetal force. SP6. The student will describe the corrections to Newtonian physics given by quantum mechanics and relativity when matter is very small, moving fast compared to the speed of light, or very large. d. Describe the gravitational field surrounding a large mass and its effect on a ray of light. What is a force? • A force is a push or pull upon an object resulting from the object's interaction with another object. • Whenever there is an interaction between two objects, there is a force upon each of the objects. • When the interaction ceases, the two objects no longer experience the force. Forces only exist as a result of an interaction. • Examples? Do the interacting objects have to touch? • Contact forces are those types of forces that result when the two interacting objects are perceived to be physically contacting each other. • Examples? • Field forces are those types of forces that result even when the two interacting objects are not in physical contact with each other, yet are able to exert a push or pull despite their physical separation. • Examples? Types and Descriptions of Forces • Applied Force – FA • A force that is applied to an object by a person or another object. • If a person is pushing a desk across the room, then there is an applied force acting upon the object. • The applied force is the force exerted on the desk by the person. Types and Descriptions of Forces • Gravitational Force – FG or FW • The force with which the earth, moon, or other massively large object attracts another object towards itself. • By definition, this is the weight of the object. • All objects upon earth experience a force of gravity that is directed "downward" towards the center of the earth. • The force of gravity on earth is always equal to the weight of the object as found by the equation FG = mg Types and Descriptions of Forces • Normal Force – FN • The support force exerted upon an object that is in contact with another stable object. • If a book is resting upon a surface, then the surface is exerting an upward force upon the book in order to support the weight of the book. • Normal forces are always PERPENDICULAR to the plane in which the objects are touching Types and Descriptions of Forces • Friction Force – FF • The force exerted by a surface as an object moves across it or makes an effort to move across it. • Friction depends upon the nature of the two surfaces and the degree to which they are pressed together. • Friction force OPPOSES the motion of an object. • If a book slides across the surface of a desk, then the desk exerts a friction force in the opposite direction of its motion. • Air resistance, or drag, is a special kind of friction that has greater effects at high speeds. Types and Descriptions of Forces • Tension Force – FT • The tension force is the force that is transmitted through a string, rope, cable or wire when it is pulled tight by forces acting from opposite ends. • The tension force is directed along the length of the wire and pulls equally on the objects on the opposite ends of the wire. Types and Descriptions of Forces • Spring Force – FSP • The spring force is the force exerted by a compressed or stretched spring upon any object that is attached to it. • An object that compresses or stretches a spring is always acted upon by a force that restores the object to its rest or equilibrium position. How do we measure forces? • Force is a quantity that is measured using the standard metric unit known as the Newton. • A Newton is abbreviated by an "N." To say "10.0 N" means 10.0 Newtons of force. • One Newton is the amount of force required to give a 1-kg mass an acceleration of 1 m/s2. • So, 1 N = 1 kgm/s2 • Weight is the measurement of force – specifically that of Earth’s gravity – on a mass. • 1 Newton is about the weight of an apple. How do we indicate forces? • A force is a vector quantity, so it has both magnitude and direction. • To fully describe the force acting upon an object, you must describe both the magnitude (size or numerical value) and the direction, usually just a sign (+/-) or a physical description (up/down or left/right). • Balanced forces cause no change in motion • Unbalanced forces do result in a change in motion How do we show how forces interact? • Free-body diagrams are diagrams used to show the relative magnitude and direction of all forces acting upon an object in a given situation. • A free-body diagram is a special example of the vector diagrams that we used earlier. The size of the arrow in a free-body diagram reflects the magnitude of the force. The direction of the arrow shows the direction that the force is acting. • Each force arrow in the diagram is labeled to indicate the exact type of force. • It is generally customary in a free-body diagram to represent the object by a box and to draw the force arrow from the center of the box outward in the direction that the force is acting. Examples: Draw FBDs for each situation 1. A textbook sits motionless on a table. 2. A coconut falls from a tree (no drag). 3. A puck slides along frictionless ice. 4. A dragster accelerates from rest. 5. A car drives at a constant velocity. 6. A block of wood slides down an incline. In 1665 Sir Isaac Newton formulated several laws that dictate the motion of objects. These laws are universal and apply to all forces in the universe. First Law of Motion – “The Law of Inertia” Second Law of Motion – “F=ma” Third Law of Motion – “The Law of Action and Reaction” Universal Law of Gravitation – “The Law of Gravity” Newton’s First Law of Motion • This law is referred to as “The Law of Inertia” because it explains how inertia is responsible for an object’s movement, or lack thereof. • Inertia is the property of matter that maintains its current status. Inertia keeps a still object still and a moving object moving. • Inertia is directly proportional to an object’s mass • This is why it is way harder to move (or stop) a heavy object. Newton’s First Law of Motion • An object at rest remains at rest, or if in motion, remains in motion at a constant velocity unless acted on by a net external force. • Net force is the sum of all forces acting on an object. Direction matters! Newton’s Second Law of Motion • This law is referred to as “F=ma” because the law is typically expressed as that formula, where: Force = mass x acceleration (N) (kg) (m/s2) • There are several relationships implied in this law: • The harder the force, the faster it will move (F ∝ a) • The bigger the object, the harder you have to push (F ∝ m) • The bigger the object, the slower it gets moving (m ∝ 1/a) Newton’s Third Law of Motion • This law is referred to as “The Law of Action and Reaction” because the law explains the interactive nature of forces. • For every action (force), there is an equal (in size) and opposite (in direction) reaction (force). • Forces are always in pairs and involve the same objects (A on B; B on A) Basic Problems and the nd 2 Law 1. What is the force on a 1000 kg elevator that is falling freely at 9.8 m/s2? 2. A net force of 16 N causes a mass to accelerate at a rate of 5 m/s2. Determine the mass. 3. What acceleration will result when a 12 N net force applied to a 3 kg object? Advanced Problems and the 2nd Law 1. A 1200kg car accelerates at 5.85 m/s2. If the force of friction acting on the car is 2800 N, how much force does the engine exert? 2. You exert a 2.45 N rightward force on a 0.500-kg cart to accelerate it across a track. If the total resistance force is 0.72 N, then what is the cart's acceleration? Advanced Problems and the 2nd Law 3. An applied force of 50 N is used to accelerate an object to the right across a frictional surface. The object encounters 10 N of friction. Use the diagram to determine the normal force, the net force, the mass, and the acceleration of the object. (Neglect air resistance.) More about friction… • There are 2 categories of friction forces – Static (FS) and Kinetic (FK) • Static friction exists while the objects are attempting to move, reaches its maximum amount right before it moves, and is then converted to kinetic friction once it moves More about friction… • Friction forces are proportional to normal forces • Greater contact forces produce more molecular interaction • Friction forces are (generally) independent of contact area • Static friction forces are ALWAYS LARGER than kinetic friction forces • Friction forces are dependent on surface texture More about friction… • The coefficient of friction is specific to the surfaces in contact, is represented by μ, and is different for static friction (μS) and kinetic friction (μK). • Typically the value ranges from 0 (frictionless) to 1, it has no unit, and it is scalar (so direction doesn’t matter) • Examples: • ice on ice – 0.02 • glass on glass – 0.9 • rubber on concrete – 0.6 More about friction… • The mathematical relationship that exists between friction forces, normal forces, and coefficients of friction is this: FF = μ FN Basic Problems with Friction 1. How much force would be required to get a 15000 N car to roll across dry concrete (μS=0.6) ? 2. If the car can be kept moving at a constant speed by applying 19000 N, what is the coefficient of kinetic friction? Advanced Problems with Friction 3. Advanced Problems with Friction 4. Newton’s Universal Law of Gravitation • • Every object with mass attracts every other object with mass. Newton realized that the force of attraction between two massive objects… • Increases as the mass of the objects increases. • Decreases as the distance between the objects increases. Newton’s Universal Law of Gravitation M1M2 • FG = G • G = Gravitational Constant • • • r2 G = 6.67x10-11 N*m2/kg2 M1 and M2 = the mass of two bodies (kg) r = the distance between them (m) Newton’s Universal Law of Gravitation • The ULoG is an inverse-square law: • • • • If the distance doubles, the force drops to 1/4. If the distance triples, the force drops to 1/9. Distance x 10 = FG / 100 There is a gravitational force between you and the person next to you, but it is dwarfed by the force between you and the earth. Why? Newton’s Universal Law of Gravitation ■ Jimmy is attracted to Betty. Jimmy’s mass is 90.0 kg and Betty’s mass is 57.0 kg. If Jim is standing 10.0 meters away from Betty, what is the gravitational force between them? ■ FG = GM1M2 / r2 ■ FG = (6.67x10-11 Nm2/kg2)(90.0 kg)(57.0 kg) / (10.0 m)2 ■ FG = (3.42x10-7 Nm2) / (100. m2) ■ FG = 3.42x10-9 N = 3.42 nN ■ In standard terms, that’s 7.6 ten-billionths of a pound of force. Newton’s Universal Law of Gravitation ■ The Moon is attracted to the Earth. The mass of the Earth is 6.0x1024 kg and the mass of the Moon is 7.4x1022 kg. If the Earth and Moon are 345,000 km apart, what is the gravitational force between them? Newton’s Universal Law of Gravitation ■ Gravitational field – an area of influence surrounding a massive body. ■ ■ g = GM / r2 ■ ■ ■ Field strength = acceleration due to gravity (g). Notice that field strength does not depend on the mass of a second object. GM1M2/r2 = M2g = FG = Fw So gravity causes mass to have weight. Variations in Gravitational Field Strength Things Newton didn’t know… ■ ■ ■ Newton didn’t know what caused gravity, although he knew that all objects with mass have gravity and respond to gravity. To Newton, gravity was simply a property of objects with mass. Newton also couldn’t explain how gravity was able to span between objects that weren’t touching. ■ He didn’t like the idea of “action-at-a-distance”. Other things Newton didn’t know… ■ Newton didn’t know that gravity bends light. ■ ■ This was verified by a solar eclipse in 1919. He also didn’t know that gravity slows down time. ■ ■ Clocks near the surface of Earth run slightly slower than clocks higher up. This effect must be accounted for by GPS satellites, which rely on accurate time measurements to calculate your position. Einstein and Relativity ■ ■ ■ ■ Einstein’s Theory of General Relativity explains many of the things that Newtonian mechanics cannot explain. According to Einstein, massive bodies cause a curvature in space-time. Objects moving through this curvature move in locally straight paths through curved space-time. To any observer inside this curved space-time, the object’s motion would appear to be curved by gravity. Curvature of Space-Time Curvature of Space-Time Gravity…it’s not so simple anymore ■ According to Einstein, gravity isn’t technically a force. ■ ■ It’s an effect caused by the curvature of space-time by massive bodies. Why treat it as a force if it isn’t one? ■ ■ ■ Because in normal situations, Newton’s ULoG provides an excellent approximation of the behavior of massive bodies. And besides, using the ULoG is a lot simpler than using the theory of relativity, and provides results that are almost as good in most cases. So there.