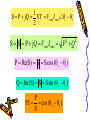Download Chapter 13 -AC - UniMAP Portal

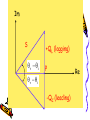
Lecture 07
AC POWER
&
POWER FACTOR
Lesson Objectives
• Compute and define apparent, reactive,
and average power for capacitors,
inductors, and resistors.
• Compute and draw the power triangle for
RC, RL, and RLC circuits.
• Define and compute the power factor for
RC, RL, and RLC circuits.
• Summarize the basic steps to compute AC
power in all or part of a circuit.
COMPLEX POWER
COMPLEX POWER
• The frequency domain
representations of the current and
voltage of an element
I  I mθi
and
V  Vm θ v
Definition of Complex Power

VI
S
2

Vm θ v I m   θ i 

2
Vm I m
S 
θ v  θ i
2
• The magnitude of S is called
the Apparent Power:
Vm I m
S
2
• Converting the complex power from
polar to rectangular form:
Vm I m
S
θ v  θ i
2

polar 
Vm I m
Vm I m
S
cos(θ v  θ i )  j
sin( θ v  θ i )
2
2
Real & Imaginary part of S
Vm I m
Vm I m
S
cos(θ v  θ i )  j
sin( θ v  θ i )
2
2
S  P  jQ
AVERAGE POWER, P
• The real part of S is called Average
Power, P. The unit is Watts.
Vm I m
P
cos(θ v  θ i )
2
REACTIVE POWER, Q
• The imaginary part of S is called
Reactive Power, Q. The unit is Var.
Vm I m
Q
sin( θ v  θ i )
2
• The complex power may be expressed
in terms of the load impedance, Z:

VI

S
 Vrms I rms
2
Vrms
where, Z 
θ v  θ i
I rms
 Vrms  I rms Z
S in terms of Z
Therefore,

rms rms
S V I
 I rms Z 
2
Vrms
Z

2
AVERAGE POWER
AC AVERAGE POWER
P  Veff I eff cos 
where;
  v i
• Average power is independent of
whether v leads i, or i leads v.
Average Power in RESISTOR
• Since ||=0o and cos (0o) =1
PR  Veff I eff cos0
2
eff
V
Vm I m
2
P
 Veff I eff 
 I eff R
2
R
Average Power in L and C
• PAV in a capacitor and inductor
is 0, since;
|C|= |L|= 90o and cos (90o) =0.
PL / C  Veff I eff cos90  0
REACTIVE POWER
REACTIVE POWER, Q
• The reactive power, Q is given by:
Vm I m
Q
sin( θ v  θ i )
2
• Reactive power repeatedly stored
and returned to a circuit in either a
capacitor or an inductor.
2
L
V
Q  VI  I X 
XL
2
L
or
2
C
V
Q  VI  I X 
XC
2
C
Q For Various Load
• Q = 0 for resistive load
• Q > 0 for inductive load
• Q < 0 for capacitive load
POWER FACTOR
POWER FACTOR
• The factor that has the significant
control over the delivered power level is
the cos (), where:
  v i
• No matter what level I and V are, if:
cos ()=0, >> the power delivered is zero.
cos ()=1, >> the power delivered is max.
POWER FACTOR
• Power Factor equation:
P
Fp  cos   
Veff I eff
• where,
  v i
Power Factor Leading or
Lagging?
• Inductive circuits have lagging power
factors.
• Capacitive circuits have leading power
factors.
• Power factors follow the current.
• Remember ELI and ICE
Ex.
• Find power factor if,
i  2 sin t  20 ;
v  50 sin t  40
Sinusoidal shift to the right
Sinusoidal shift to the left
Solution
Fp  cos(  v  i ) 
cos 40  (20)   0.5 lagging
Lagging because current is lagging and ELI.
POWER TRIANGLE
Power Triangle and Apparent
Power
• The impedance triangle with R, X, and
Z may be shown to be similar to the
power triangle with P, Q, and S,
respectively as components.
• Apparent power – A useful quantity
combining the vector sum of P and Q.
Recall the Impedance Triangle
XL
Z

R
The Power Phasor
I2XL
I2 Z

I2 R
The Power Triangle
S

P
QL
Im
S
θ v  θi
+QL (lagging)
P
θ v  θi
-QC (leading)
Re
SUMMARY OF POWER
IMPORTANCE OF S
• S contains all power of a load.
• The real part of S is the real power, P
• Its imaginary part is the reactive
power, Q.
• Its magnitude is the apparent power
• The cosine of its phase angle is the
power factor, pf.
1 
S  P  jQ  VI  Vrms I rms v   i
2
S  S  P  jQ  Vrms I rms  P  Q
2
P  Re(S)  S  S cos (θ v  θi )
Q  Im (S)  S  S sin (θ v  θi )
P
Pf   cos (θ v  θ i )
S
2
Review Quiz
• Name the three types of power.
• Q has units of … ?
P has units of … ?
S has units of … ?
• Formula for P,Q,S… ?
• Power factor is … ?
• T/F: Power factor can never be greater
than one or less than zero.