Download Chapter 4 Bohr`s model of the atom

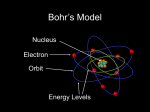
Chapter 4 Bohr’s model of the atom
4.1 Thomson’s model (plum pudding)
(1) An atom in which the negatively charged electrons were located within
a continuous distribution of positive charge.
(2) At its lowest energy state, the electrons would be fixed at their
equilibrium positions.
(3) In excited atoms, the electrons would vibrate about their
equilibrium positions.
Plum pudding
(4) A vibrating electrons emit electromagnetic radiation.
 A Thomson hydrogen atom has only one characteristic emission
frequency conflict with the very large number of different frequencies
observed in the spectrum of hydrogen.
Chapter 4 Bohr’s model of the atom
Rutherford : The positive charge (nucleus) is concentrated in a very small
region. (1908 Nobel prize for the chemistry of the radioactive substances)
α particle scattering
N: the number of atoms that deflect an α particle
θ: the angle of deflection in passing through one atom
Θ: the net deflection in passing through all the atoms
(  2 )1 / 2 
N ( 2 )1 / 2
2 I   2 /  2
e
d is the number of  particle scattered
2

within the angular range  to   d
N ( )d 
r  10 10 m    10-4 rad
by Thomson' s model prediction
Chapter 4 Bohr’s model of the atom
6
Ex: In a typical experiment, α particles were scattered by a gold foil 10 m
thick. The average scattering angle was found to be (  2 )1 / 2  1o  2  102 rad
Calculate ( 2 )1 / 2
(a) the number of atoms N  10 6 m/ 10 10 m  10 4
(  2 )1 / 2 2  10  2
( ) 

 2  10  4 rad
2
10
N
agree with the Thomson' s atom estimation
2 1/ 2
(b) the fraction of  particle scattering :
experiment al prediction : N(  90 o ) / I  10  4
theoretica l prediction for Thomson' s atom :
N(  90 ) / I 
o

180o
90o
N( )d / I  e  ( 90)  10  3500
2
 An atom has a very small nucleus with positive charge.
Thomson’s atom model must be corrected.
Chapter 4 Bohr’s model of the atom
4.2 Rutherford’s model
All the positive charge of the atom, and consequently essentially all its mass, are
assumed to be concentrated in a small region in the center called the nucleus
(1) Nucleus radius: Thomson : r  10 10 m
Rutherford : r  10 14 m
(2) Maximum deflection angle: Thomson :   10 4 rad
Rutherford :   1 rad
Chapter 4 Bohr’s model of the atom
α particle scattering trajectory
b: impact parameter
M: α particle mass
v : incident particle velocity
total angular momentum conservati on : Mvb  Mv 'b'  L
2
total kinetic energy conservati on : Mv 2 / 2  Mv ' / 2
 v  v '  b  b'
The scattering trajectory of a light positive +ze particle by a heavy
nucleus +Ze can be solved by Newton’s law.

zZe 2
d 2r
d 2

F  ma 

M
[

r
(
) ]
4 0 r 2
dt 2
dt
Chapter 4 Bohr’s model of the atom
d 2 r / dt 2 : the radial acceleration
 r (d / dt )2   2 r : the centripetal acceleration
r  1/ u 
dr
dr d dr du d
1 du
L du


 2

dt d dt
du d dt
u d
M d
d 2r
d dr d
L d 2 u Lu 2
L2 u 2 d 2 u

( )


put into (1)
dt 2
d dt dt
M d 2 M
M 2 d 2
L2 u 2 d 2 u 1 Lu 2 2 zZe 2 u 2

 (
) 
2
2
M d
u M
4 0 M
d 2u
zZe 2 M
zZe 2 M
2
2


u




set
D

(
zZe
/
4


)
/(
Mv
/ 2)
0
2
2
2 2 2
d
4 0 L
4 0 M v b
d 2u
D


u


the solution is u  A cos   B sin   D / 2b 2
2
2
d
2b
for coefficients A and B  consider the initial condition :
(1)   0 as r   (2) dr / dt   v as r  
 u  1 / r  0  A cos 0  B sin 0  D / 2b 2  A  D / 2b 2
Chapter 4 Bohr’s model of the atom
dr
L du
L

 v  
(  A sin 0  B cos 0)
dt
M d
M
Mv
Mv
1
B


L
Mvb b
D
1
D
the solution is u 
cos


sin


2b 2
b
2b 2
1 1
D
the scattering trajectory is
 sin   2 (cos   1)
r b
2b
 2b
as r   and set       cot 
- - - - - - - (2)
2
D
 -
1 1
 
D
 
the closest distance R ( for  
)
 sin(
)  2 [cos(
)  1]
2
R b
2
2b
2
D
1
from (2)  R  [1 
]
2
sin( / 2)
head - on collision :     b  0
no deflection :   0  b   and R  
Chapter 4 Bohr’s model of the atom
the number N (  )d scattered into  to   d
 the number incident from b to b  db
area of incident ring : 2bdb
the number of ring : t
scattering probabilit y : P (b )db  t 2bdb
D d / 2
2 sin 2 ( / 2)

d
 P (b )db   tD 2 sin 
8
sin 4 ( / 2)
 P (b )db is the scattering probabilit y from  to   d
N ( )d

sin d

  P ( b )db  tD 2
I
8
sin 4 ( / 2)
from (2)  db  
R180o
zZe 2
D
 the nucleus radius
4 0 ( Mv 2 / 2)
Chapter 4 Bohr’s model of the atom
rnuleus  10 14 m
d
d
Ind
: differenti al cross section
d
d
d  2 sin d
dN 
zZe 2 2
1
 N ( )d  dN  (
) (
)
Ind
2
4
4 0
2 Mv
sin (  / 2)
1
2
Rutherford scattering differenti al cross section :
d
1 2 zZe 2 2
1
(
) (
)
d
4 0
2 Mv 2 sin 4 ( / 2)
Chapter 4 Bohr’s model of the atom
4.3 The stability of the nuclear atom
The serious difficulties in the previous atomic model:
(1) The charged electrons constantly accelerate in their motion around
the nucleus, radiate energy in the form of electromagnetic radiation.
The atom would rapidly collapse to nuclear dimension.
(2) The continuous spectrum of radiation is not in agreement with the
discrete spectrum observed in experiments.
4.4 Atomic spectra
An apparatus for
measuring atomic spectra
Chapter 4 Bohr’s model of the atom
n2
Balmer (1885) :   3646 2
ex : n  3( H  ), n  4( H  )
n 4
1
1
1
Ryberg (1890) :    RH ( 2  2 ) n  3,4..

2
n
RH  1.097  10 7 m -1 : Ryberg constant for H
For alkali elements (Li, Na, K,...) :
κ
1
1
1
 R[

]
λ
( m  a )2 ( n  b)2
Chapter 4 Bohr’s model of the atom
4.5 Bohr’s postulate
Bohr’s postulate (1913):
(1) An electron in an atom moves in a circular orbit about the nucleus under
the influence of the Coulomb attraction between the electron and the
nucleus, obeying the laws of classical mechanics.
(2) An electron move in an orbit for which its orbital angular momentum
is L  n  nh / 2 , n  1,23.., h Planck’s constant
(3) An electron with constant acceleration moving in an allowed orbit does not
radiate electromagnetic energy. Thus, its total energy E remains constant.
(4) Electromagnetic radiation is emitted if an electron, initially moving in an
orbit of total energy Ei, discontinuously changes its motion so that it moves
in an orbit of total energy Ef. The frequency of the emitted radiation
is   ( E i  E f ) / h .
Chapter 4 Bohr’s model of the atom
4.6 Bohr’s model
Ze 2
v2
m
for L  mvr  n , n  1,2,3...
4 0 r 2
r
1
n 2
n 2 2
 Ze  4 0 mv r  4 0 mr (
)  4 0
mr
mr
n 2 2
 r  4 0
mZe 2
n
1 Ze 2
 v

mr 4 0 n
2
2
Potential energy : V   

r
Ze 2
Ze 2
dr  
4 0 r 2
4 0 r
ground state
1
Ze 2
2
Kinetic energy : K  mv 
2
4 0 2r
Ze 2
mZ 2 e 4
1
Total energy : E  K  V  


K

E


(4 0 ) 2 2r
( 4 0 ) 2 2 2 n 2
Chapter 4 Bohr’s model of the atom
 
Ei  E f
(

h
1
Pachen
2
4 0
1


)2
4
mZ e
1
1
(

)
4 3 n 2f ni2

Lyman
c
me 4 Z 2 1
1
(
)
(

)
3
2
2
4 0
4 c n f ni
1
 R Z 2 (
Balmer
2
1
1

)
n 2f ni2
me 4
for R  (
)
 RH
4 0 4 3 c
1
2
Chapter 4 Bohr’s model of the atom
4.7 Correction for finite nuclear mass
the reduced mass of the system :  
mM
mM
 L  vr  n
   RM Z 2 (
1
1

)
n 2f ni2
M

M
R 
R , RM  R , as

mM
m
m
M
For hydrogen atom :
 1836
m
1
 RM 
R
2000
RM 
Chapter 4 Bohr’s model of the atom
Ex: The positronium atom, consisting of a positron and an electron
revolving about their common center of mass, which lies halfway
between them. (a) In such system were a normal atom, how would its
emission spectrum compare to that of the hydrogen atom? (b) What
would be the electron-positron separator, D, in the ground state orbit
of the positronium.
mM
m2 m
m
R



RM 
R  
m  M 2m
2
mm
2
RM hcZ 2
R hcZ 2
E positronium  

n2
2n 2
1 
R
1
1
     Z 2( 2  2 )
 c
2
n f ni
the electron - positron separator D in ground state is :
Dpositronium
4 0 n 2  2
4 0 n 2  2

2
 2rhydrogen
Ze 2
mZe 2
Chapter 4 Bohr’s model of the atom
Ex: A muonic atom contains a nucleus of charge +Ze and a negative muon μmove about it, The μ- is an elementary particle with charge –e and a mass that
is 207 times as large as an electron mass. (a) Calculate the muon-nucleus
separation, D, of the first Bohr orbit of a muonic atom with Z=1. (b) Calculate
the binding energy of a muonic atom with Z=1. (c) What is the wavelength of
the first line in the Lyman series for such an atom?
(a) m    207me , M  1836me

Dn 1
207me  1836me
 186me
207me  1836me
o
4 0  2
1
3
11
 5.3  10 m  2.8  10 A


2
186
186me e
me e 4
 186  13.6 eV  2530 eV
(b) E  186
(4 0 ) 2 2 2
is the ground state energy. The binding energy is 2530 eV.
o
1
1
1
1
 RM ( 2  2 )  186 R (1  )  139.5 R    6.5 A
(c)  
4
n f ni

Chapter 4 Bohr’s model of the atom
Ex: Ordinary hydrogen contains about one part in 6000 of deuterium, or heavy
hydrogen. This is a hydrogen atom whose nucleus contains a proton and a
neutron. How does the doubled nuclear mass affect the atomic spectrum?

R
109737 cm 1
RH  R


 109678 cm 1
m (1  m / M ) (1  1 / 1836)

R
109737 cm -1
RD  R


 109707 cm -1
m (1  m / M ) (1  1/2  1836)
RD  RH   D   H   D   H
The spectral lines of the deuterium atom are shifted
to slightly shorter wavelength s compared to hydrogen.
Chapter 4 Bohr’s model of the atom
4.8 Atomic energy states
Franck -Hertz experiment (1914): the quantized atomic energy
9.8 eV
Hg
V : accelerating potential
Vr : retarding potential
4.9 eV
Energy level
of Hg vapor
Chapter 4 Bohr’s model of the atom
4.8 Interpretation of the quantization rules
Some Mysteries:
Bohr’s quantization of the angular momentum?
Planck’s quantization of the energy?
Wilson-Sommerfeld quantization rules:
For every physical system in which the coordinates are periodic
functions of time, there exists a quantum condition for each
coordinate. The quantum conditions are  pq dq  nq h
q:
one of the coordinate
pq : the momentum associated with the coordinate q
nq : the integer quantum number

: the integration over one period of the coordinate q
Chapter 4 Bohr’s model of the atom
For one-dimensional simple harmonic oscillation:
x ( t )  A cos t 
 a( t ) 
dx ( t )
 A sin t  v ( t )
dt
dv ( t )
  2 A cos t
dt
 F  a ( t )m   kx ( t )   2 m  k   
k
 2 
m
p x2 kx 2
p x2
x2
E  K V 



1
2m
2
2mE 2 E / k
p x2 x 2

 1 for b  2mE , a  2 E / k
b2 a 2
 p dx  ab  
x
2mE
2 E / k  2E / 
 E /   n x h  nh  E  nh
E  E ( n  1)  E ( n)  ( n  1)h  nh  h
h  0  E  0 continuous energy
Chapter 4 Bohr’s model of the atom
The angular momentum quantization for Bohr’s atom:
 p dq  n h   Ld  L
q
q
2
0
d  2L
nh
 n
2
nh
 L  mvr  pr  n 
2
 2L  nh  L 
for de Broglie wavelength   

h

r
h
h
 p
p

nh
 2r  n , n  1,2,3...
2
de Broglie standing wave
Chapter 4 Bohr’s model of the atom
4.10 Sommerfeld’s model
Fine structure: a splitting of spectral lines due to spin-orbit interaction
Sommerfeld’s explanation for an elliptical orbit:
 Ld  n h  L2  n h  L  n / , n  1,2,3..
 p dr  n h  L(a / b  1)  n h, n  0,1,2,...
r
r
r
r
4 0 n 2  2
n
1 2 Z 2 e 4
a
,b  a
 E  (
)
Ze 2
n
4 0 2n 2  2
 : reduced mass
nr : radial quantum number
n : azimuthal quantum number
n  nr  n principal quantum number
(1) n  n circular orbit
(2) n  nr elliptical orbit
 For the same n, but different nr and n energy is degenerate.
Chapter 4 Bohr’s model of the atom
 Sommerfeld removed the degeneracy by treating the problem relativistically.
for hydrogen atom v / c  102
 E  (v / c )2  10 4 (eV) energy splitting
Z 2 e 4
 2Z 2 1
3
E
[
1

(

)]
2
2 2
(4 0 ) 2n 
n
n 4n
e2
1


fine structure constant
4 0 c 137
1
Selection rule:
ni  nf  1
Chapter 4 Bohr’s model of the atom
4.11 The correspondence principle
Bohr (1923):
(1) In a limit of very large quantum number, the prediction of quantum
theory corresponds to that of classical theory.
(2) Any selection rule hold true in the quantum theory, which also apply in
the classical limit (very large quantum number).
Ex: blackbody radiation:
Planck' s theory :   nh    n h
Classical theory :  0    kT constant

n h  kT as   0 and h  0  n  
Chapter 4 Bohr’s model of the atom
Ex: Apply the correspondence principle to hydrogen atom radiation in the
classical limit.
The classical radiation frequency of  0 in Bohr orbit n is
v
1 2 me 4 2
0 
(
)
2r
4 0 4 3 n 2
Bohr' s radiation theory for ni  n f  1
me 4
1
1
1 2 me 4
2n  1
 (
)
[

]

(
)
[
]
3
2
2
3
2 2
4 0 4 ( n  1)
n
4 0 4 ( n  1) n
1
2
me 4 2
n     (
)
0
4 0 4 3 n 2
1
2
 Transitions are observed to occur between states of low n, in which the old
quantum theory cannot always be made to agree with experiment.
Chapter 4 Bohr’s model of the atom
4.12 A critique of the old quantum theory
(1) The Wilson-Sommerfeld quantization is just used to treat the periodic
system
(2) It can be used to calculate the energy of the allowed states, but cannot be
used to calculate the transition rate.
(3) It is successful only for one-electron system, fails badly for two (many)
electron.
(4) The entire theory seems to lack coherence.