Download Powerpoint

AVL Balanced Trees
Introduction
Data structure
AVL tree balance condition
AVL node level
AVL rotations
Choosing the rotation
Performing a balanced insertion
Outputting data
Testing and results

Introduction 1
There is no reason why a Knuth binary tree should balance.
Average performance for random input should not be greatly
below balanced performance, but if the tree is made from
sorted input, it will degrade to a linked list with access time of
O(N) where there are N nodes. Access time for a node within
a balanced tree will be log2N or slightly less.
Operations which change the balance of a tree are insertion
and deletion. Insertion might increase the maximum depth of
a tree, but deletion can't do this.
Therefore, if effort is going to be expended in balancing an
unbalanced tree, by rearranging nodes, this can initially be
most usefully applied following insertion of nodes.
Introduction 2
A perfectly balanced tree can only exist if N is 2x1 where x is
an integer, i.e. if N is a value the series 1, 3, 7, 15, 31, 63,
127, 255 ... . The need for perfect balance could be relaxed by
allowing the bottom level of the tree to be partially filled.
This is difficult to achieve, as the entire tree might need
rearranging after every insertion and deletion.
The imbalance problem only arises within the path through
the tree on which a node is inserted. A recursive insertion
function will return upwards through the insertion path. If
information about the maximum depths of nodes is
maintained as part of each nodes structure, it is possible to
correct imbalances through localised rearrangements
following insertion on the recursive return path upwards to
the root.
Data Structure
AVL Tree Balance Condition
A particular approach to performing the tree rearrangements
needed to keep a tree balanced was designed by AdelsonVelskii
and Landis and named as the AVL tree.
An AVL tree has a balance condition such that each node stores
the maximum depth of nodes below it. A NULL tree has a level
of 1 and a leaf node has a level of 0. A node having 1 or 2
subtrees will have as its own level the maximum of left or right
subtree levels +1. Within an AVL tree, the maximum difference
allowed between left and right subtree levels is 1. When an
insertion or deletion operation results in this difference
increasing to 2, rearrangements called rotations are performed
to reduce the imbalance for an AVL tree to retain the AVL
balance condition.
AVL Node Level
Following an insertion or deletion which may influence the levels of
subtrees, the level of nodes affected will need to be recalculated. This
can be achieved using a function operating on the above data
structure as follows:
AVL Rotations
A difference of levels between left and right subtrees
can be increased, through insertion of a new node into
the tree, in one of 4 possible ways:
1. Insertion into left subtree of left branch.
2. Insertion into right subtree of left branch.
3. Insertion into left subtree of right branch.
4. Insertion into right subtree of right branch.
The function prototype for a rotation will be of
theform:
void rotN(TOP *t); /* N is rotation type 1-4 */
Rotation case 1
Rotation case 1
Rotation case 2
Rotation case 2
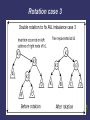
Rotation case 3
Rotation case 3
Rotation case 4
Rotation case 4
Choosing the rotation slide 1
The rotation type 1 4 can be determined by comparing 3 keys, the key
inserted and the child and parent key. It is useful to have a 2 way
comparison function similar to the strcmp() function in string.h.
Choosing
the
rotation
slide 2
Calling the rotation
Performing an AVL balanced insertion 1 of 3
Performing an AVL balanced insertion 2 of 3
Performing an AVL balanced insertion 3 of 3
Output of AVL organised data 1
Printing the entire tree can be done recursively in
search order. It is useful when debugging to be able to
identify the immediate left and right child nodes for
each record printed.
#define DEBUG 1 /* or 0 for less noisy output */
Using a printdata function enables the printall function
to be data independent.
void printdata(DATA d){ /* prints DATA item d */
printf("%c ",d);
}
Output of AVL organised data 2
Testing code
Test Results
AVL imbalance : -2 AVL type: 4
AVL imbalance : -2 AVL type: 3
AVL imbalance : 2 AVL type: 2 ...
o insert: duplicate key error
... (run the program avltree.c to see full o/p)
a0
ab2c
c1d
d0
be3g
f0
fg1h
h0
ei4k
j0
jk2m
l0
lm1
in5u
o1p
p0
oq2s
r0
rs1t
t0
qu3w
v0
vw2y
x0
xy1z
z0
These results show in 4 columns per node:
i. The left child key or blank. ii. The node key.
iii. The node level.
iv. The right key or blank.
Recommended Reading
"Data Structures and Algorithms in C",
Mark Allen Weiss, Addison Wesley Chapter 4.