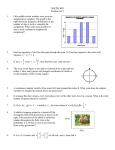
Download The problems in this booklet are organized into strands. A

 The problems in this booklet are organized into strands. A
problem often appears in multiple strands. The problems are
suitable for most students in Grade 11 or higher.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
What’s Your Angle?
E
A
C
B
F
A is the centre of a circle which passes through B. B is the centre of a circle
which passes through A. CAE and CBF are straight line segments.
If ∠F = 78◦ , determine the measure of ∠C.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
What’s Your Angle?
Problem
E
x
A is the centre of a circle which passes through B.
B is the centre of a circle which passes through
A. CAE and CBF are straight line segments. If
∠F = 78◦ , determine the measure of ∠C.
A
y
C
x
y
78
B
Solution
Construct AB and BE. A, E and F are on the circumference of the circle with
centre B. Therefore, BA = BE = BF .
In 4BEF , BE = BF . Then 4BEF is isosceles and ∠BEF = ∠F = 78◦ .
Let x = ∠BEA and y = ∠ABC.
In 4BAE, BA = BE and the triangle is isosceles. Therefore,
∠BAE = ∠BEA = x.
Since B and C are on the circle with centre A, AC = AB and 4ABC is
isosceles. Therefore, ∠C = ∠ABC = y.
∠EAB is an exterior angle to 4ABC. By the exterior angle theorem for
triangles, ∠EAB = ∠C + ∠ABC. But ∠EAB = x and
∠C + ∠ABC = y + y = 2y. Therefore, x = 2y.
In 4CEF ,
∠C + ∠E + ∠F = 180◦
∠C + ∠CEB + ∠BEF + 78◦ = 180◦
y + x + 78◦ + 78◦ = 180◦
But x = 2y,
∴ y + 2y + 156◦ = 180◦
3y = 24◦
y = 8◦
Therefore, ∠C = 8◦ .
F
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Love is in the Air
In Mr. Vee’s Physics class, each student gave every other student a valentine.
Mr. Vee did not give or receive any valentines. The girls received a total of 540
valentines and the boys received a total of 390 valentines.
How many students are in Mr. Vee’s class? How many girls are in the class?
How many boys are in the class?
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Love is in the Air
Problem
In Mr. Vee’s Physics class, each student gave every
other student a valentine. Mr. Vee did not give or
receive any valentines. The girls received a total of
540 valentines and the boys received a total of 390
valentines. How many students are in Mr. Vee’s
class? How many girls are in the class? How many
boys are in the class?
Solution
Let n represent the number of students in Mr. Vee’s class.
Each student sends n − 1 valentines and the total number of valentines sent is
540 + 390 or 930 valentines. So the number of students, n, times the number of
valentines sent, n − 1, equals the total number of valentines.
n(n − 1) = 930
n2 − n − 930 = 0
(n − 31)(n + 30) = 0
n = 31 or n = −30 but n > 0, ∴ n = 31
Therefore, there are 31 students in the class and each student sent 30
valentines and received 30 valentines.
Since the girls received a total of 540 valentines and each student received 30
valentines, there are 540 ÷ 30 or 18 girls in the class.
Since the boys received a total of 390 valentines and each student received 30
valentines, there are 390 ÷ 30 or 13 boys in the class.
Mr. Vee’s class has 31 students, 18 girls and 13 boys.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
How Many Children Are There Anyway?
A man died leaving some money in his estate. All of this money was to be
divided among his children in the following manner:
$x to the first born plus
1
16
of what remains, then
$2x to the second born plus
$3x to the third born plus
1
16
1
16
of what then remains, then
of what then remains, and so on.
When the distribution of the money was complete, each child received the
same amount and no money was left over. Determine the number of children.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
How Many Children Are There Anyway?
Problem
A man died leaving some money in his estate. All of this money was to be divided among his
1
children in the following manner: $x to the first born plus 16
of what remains, $2x to the
1
1
of what then remains,
second born plus 16 of what then remains, $3x to the third born plus 16
and so on. When the distribution of the money was complete, each child received the same
amount and no money was left over. Determine the number of children.
Solution
Let T be the total value of the estate. T > 0 since there is money in the estate.
Let y be the amount of money given to each child. y > 0 since each child receives money.
Then Ty is the number of children.
The first child receives x to begin with. There would be (T − x) left at this point. The first
1
child then receives 16
of the remaining amount (T − x). Therefore, the first child receives
1
(T − x).
y = x + 16
The second child receives 2x to begin with. There would now be (T − y − 2x) left in the estate.
This represents the original amount minus the first child’s full share minus the amount received
1
of the remaining amount
so far by the second child. The second child then receives 16
1
(T − y − 2x). Therefore, the second child receives y = 2x + 16 (T − y − 2x).
But each child receives the same amount.
1
1
∴ x + (T − x) = 2x + (T − y − 2x)
16
16
1
1
1
1
1
x + T − x = 2x + T − y − (2x)
16
16
16
16
16
1
1
2
x − x = 2x − y − x
16
16
16
Multiply each side of the equation by 16.
16x − x = 32x − y − 2x
15x = 30x − y
y = 15x
Therefore each child receives $15x.
(The solution continues on the next page.)
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Substituting 15x for y into the equation y = x +
x+
1
(T
16
− x) we obtain
1
(T − x) = 15x
16
1
(T − x) = 14x
16
T − x = 224x
T = 225x
Therefore the total value of the estate is 225x.
We can now determine the number of children
T
y
=
225x
15x
= 15.
Therefore the father had 15 children.
Notice, we did not need to know T , the total value of the estate. It turns out that once we
know x, we can determine each child’s share, 15x, and the total value of the estate, T = 225x.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Find the Number
Five different numbers, a, b, c, d, and e, are written in order smallest to largest
such that a < b < c < d < e. When the numbers are added in pairs the
following sums are obtained: 726, 756, 770, 781, 795, 816, 825, 830, 860 and 885.
Determine the sum of the five numbers and determine the value of the smallest
number, a.
!!
$
"!
$
#!
$
&! $
%!
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Find the Number
Problem
Five different numbers, a, b, c, d, and e, are written in order smallest to largest
such that a < b < c < d < e. When the numbers are added in pairs the
following sums are obtained: 726, 756, 770, 781, 795, 816, 825, 830, 860 and 885.
Determine the sum of the five numbers and determine the value of the smallest
number, a.
Solution
We know the sum of each pair so we can determine the sum of all of the sums.
(a+b)+(a+c)+(a+d)+(a+e)+(b+c)+(b+d)+(b+e)+(c+d)+(c+e)+(d+e)
= 4a + 4b + 4c + 4d + 4e
= 726 + 756 + 770 + 781 + 795 + 816 + 825 + 830 + 860 + 885
= 8 044
Therefore 4a + 4b + 4c + 4d + 4e = 8 044. Dividing each side of the equation by
4, we obtain a + b + c + d + e = 2 011. That is, the sum of the five numbers is
2 011.
The smallest sum is created by adding the two smallest numbers. Therefore,
a + b = 726. The largest sum is created by adding the two largest numbers.
Therefore, d + e = 885. If we subtract the sum of the two smallest numbers
and the sum of the two largest numbers from the total sum, we will get the
middle number, c.
(a + b + c + d + e) − (a + b) − (d + e) = 2 011 − 726 − 885
∴ c = 400
The second smallest sum is created by adding the smallest number, a, to the
middle number, c. (A justification of this statement is shown on the next
page.) Therefore, a + c = 756 and a = 756 − c = 756 − 400 = 356.
The sum of the five numbers is 2 011 and the smallest number is 356. The
complete list is 356, 370, 400, 425 and 460. It is left as an exercise for the
student to verify the correctness of this list.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Why is a + c is the second smallest sum?
We know that a < b < c < d < e so the following is true:
1. Since b > a, let b = a + m, m > 0.
2. Since c > b, c = b + n = a + m + n, m, n > 0.
3. Since d > c, d = c + p = a + m + n + p, m, n, p > 0.
4. Since e > d, e = d + q = a + m + n + p + q, m, n, p, q > 0.
We need to show that a + c > a + b and a + c is smaller than all other possible sums. So now
let’s look at the ten possible sums:
1. a + b = a + a + m = 2a + m.
2. a + c = a + a + m + n = 2a + m + n > 2a + m = a + b.
So a + c > a + b.
3. a + d = a + a + m + n + p = 2a + m + n + p > 2a + m + n = a + c.
So a + d > a + c.
4. a + e = a + a + m + n + p + q = 2a + m + n + p + q > 2a + m + n = a + c.
So a + e > a + c.
5. b + c = a + m + a + m + n = 2a + 2m + n > 2a + m + n = a + c.
So b + c > a + c.
6. b + d = a + m + a + m + n + p = 2a + 2m + n + p > 2a + m + n = a + c.
So b + d > a + c.
7. b + e = a + m + a + m + n + p + q = 2a + 2m + n + p + q > 2a + m + n = a + c.
So b + e > a + c.
8. c + d = a + m + n + a + m + n + p = 2a + 2m + 2n + p > 2a + m + n = a + c.
So c + d > a + c.
9. c + e = a + m + n + a + m + n + p + q = 2a + 2m + 2n + p + q > 2a + m + n = a + c.
So c + e > a + c.
10. d + e = a + m + n + p + a + m + n + p + q = 2a + 2m + 2n + 2p + q > 2a + m + n = a + c.
So d + e > a + c.
So we have shown that a + c > a + b and a + c is smaller than the eight other possible sums.
Therefore, a + c is the second smallest sum. (It is also possible to use the above information to
show that c + e is the second largest sum.)
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
A Problem For The Ages
A four-digit number which is a perfect square is created by writing Jennifer’s
age in years followed by John’s age in years. Similarly, in 31 years, their ages in
the same order will again form a four-digit perfect square.
How old are Jennifer and John today?
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
A Problem For The Ages
Problem
A four-digit number which is a perfect square is created by writing Jennifer’s age in years
followed by John’s age in years. Similarly, in 31 years, their ages in the same order will again
form a four-digit perfect square. How old are Jennifer and John today?
Solution
Both Jennifer’s age and John’s age must be two digit numbers. If Jennifer’s age is a one-digit
number, John’s age would have to be a three-digit number to create the four-digit perfect
square. But in 31 years, Jennifer’s age would then be a two-digit number resulting in at least a
five-digit number when their ages are used to form the second perfect square. A similar
argument could be presented if John’s age is a one-digit number. Therefore, both Jennifer and
John have ages that are each two-digit numbers.
Let Jennifer’s present age be x and John’s present age be y. Then 100x + y is the four digit
number created by writing Jennifer’s age followed by John’s age. But 100x + y is a perfect
square so let 100x + y = k 2 , for some positive integer k.
In 31 years, Jennifer will be (x + 31) and John will be (y + 31). The new number created by
writing Jennifer’s age followed by John’s age is 100(x + 31) + (y + 31). This new four-digit
number is also a perfect square. So 100(x + 31) + (y + 31) = m2 , for some positive integer
m, m > k. This simplifies as follows:
100x + 3100 + y + 31 = m2
100x + y + 3131 = m2 (1)
From our work above, we also have 100x + y = k 2 . Substituting this into (1) we get
k 2 + 3131 = m2 or 3131 = m2 − k 2 . m2 − k 2 is a difference of squares, so
m2 − k 2 = (m + k)(m − k) = 3131.
Since m and k are positive integers, m + k is positive and m + k > m − k. m − k must also be
positive since (m + k)(m − k) = 3131. So we are looking for two positive numbers that
multiply to 3131. There are two possibilities, 3131 × 1 or 101 × 31.
First we will examine (m + k)(m − k) = 3131 × 1. From this we obtain two equations in two
unknowns, namely m + k = 3131 and m − k = 1. Subtracting the two equations gives
2k = 3130 or k = 1565. Then k 2 = 15652 = 2449225. This is not a four-digit number so
3131 × 1 is not an admissible factorization of 3131.
Next we examine (m + k)(m − k) = 101 × 31. This leads to m + k = 101 and m − k = 31.
Subtracting the two equations we get 2k = 70 or k = 35. Then 100x + y = k 2 = 1225.
Therefore, x = 12 and y = 25 since 1225 is the four-digit number formed by writing Jennifer’s
age, x, followed by John’s age, y.
∴ today Jennifer is 12 and John is 25.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Trapped!
A four-sided figure with one pair of parallel sides is called a trapezoid. An
isosceles trapezoid is one in which the non-parallel sides are equal in length.
D
A
x
x
O
B
C
Isosceles trapezoid ABCD has parallel sides AD and BC and sides
AB = DC = x. The area of the trapezoid is 510 cm2 . A circle with centre O
and radius 10 cm is contained inside the trapezoid so that it is tangent to each
of the four sides of the trapezoid.
Determine the length of x.
For purposes of this problem accept the fact that a line drawn from the centre
of a circle to a point of tangency is perpendicular to the tangent.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Trapped!
Problem
Isosceles trapezoid ABCD has parallel sides AD and BC and sides
AB = DC = x. The area of the trapezoid is 510 cm2 . A circle with centre O
and radius 10 cm is contained inside the trapezoid so that it is tangent to each
of the four sides of the trapezoid. Determine the length of x.
For purposes of this problem accept the fact that a line drawn from the centre
of a circle to a point of tangency is perpendicular to the tangent.
Solution
Draw radii OP, OQ, OR, and OS to sides AB, BC, CD, and DA,
respectively. Then OP = OQ = OR = OS = 10 since they are each radii of the
circle. Also, since each line drawn from the centre of the circle to a point of
tangency is perpendicular to the tangent,
∠OP A = ∠OQB = ∠ORD = ∠OSA = 90◦ .
Let AP = a and DR = b. Therefore, P B = x − a and RC = x − b. The
following diagram shows all of the given and found information.
A
S
a
D
b
P
R
x
x
x-a
B
O
Q
x-b
C
Join A to O forming two right triangles, 4AP O and 4ASO. Using the
Pythagorean Theorem, AP 2 = AO2 − OP 2 and AS 2 = AO2 − OS 2 . But
OP = OS since they are both radii. So the two expressions are equal and
AS = AP = a follows.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Using exactly the same reasoning that was used to show AP = AS = a, we can
show DR = DS = b, BP = BQ = x − a and CR = CQ = x − b. This new
information has been added to the diagram below.
A
a
S
b
a
D
b
P
R
x
x
O
x-a
B
x-a
Q
x-b
x-b
C
We can now find the area of the trapezoid. To find the area of a trapezoid, we
multiply the perpendicular distance between the two parallel sides by the sum
of the lengths of the two parallel sides and then divide the result by 2.
Area Trapezoid ABCD
510
510
510
510
25.5
=
=
=
=
=
=
SQ × (AD + BC) ÷ 2
(SO + OQ) × ((AS + SD) + (BQ + QC)) ÷ 2
(10 + 10) × ((a + b) + (x − a + x − b)) ÷ 2
(20) × (2x) ÷ 2
20x
x
Therefore, the length of x is 25.5 cm.
At the end of the statement of the problem, the following fact was assumed:
a line drawn f rom the centre of a circle to a point of tangency is
perpendicular to the tangent. As an extension to this problem the solver may
wish to try to prove this fact.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
The Quest For Ann Sirs?
Ann Sirs has already written three mathematics tests, worth 100 marks each.
The average of her marks on her first two tests is calculated and then averaged
with her third test mark giving an average of 86%. The average of her marks
on her second and third tests is calculated and then averaged with her first test
mark giving an average of 79.5%. The average of her marks on her first and
third tests is calculated and then averaged with her second test mark giving an
average of 81.5%.
Her fourth mathematics test is tomorrow and it is also out of 100. What mark
does Ann need on her test to achieve an overall average of 85% in her
mathematics course?
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
The Quest For Ann Sirs?
Problem
Ann Sirs has already written three mathematics tests, worth 100 marks each. The average of
her marks on her first two tests is calculated and then averaged with her third test mark giving
an average of 86%. The average of her marks on her second and third tests is calculated and
then averaged with her first test mark giving an average of 79.5%. The average of her marks on
her first and third tests is calculated and then averaged with her second test mark giving an
average of 81.5%. Her fourth mathematics test is tomorrow and it is also out of 100. What
mark does Ann need on her test to achieve an overall average of 85% in her mathematics
course?
Solution
Let a represent Ann’s first mark, b represent Ann’s second mark, c represent Ann’s third mark
and d represent Ann’s fourth mark.
When the average of her first and second marks is averaged with her third test mark, the new
a+b
+c
+ c = 172. Multiplying by 2 again
average is 86 so 2 2 = 86. Multiplying by 2 gives a+b
2
yields a + b + 2c = 344. (1)
When the average of her second and third marks is averaged with her first test mark, the new
b+c
+a
+ a = 159. Multiplying by 2 again
average is 79.5 so 2 2 = 79.5. Multiplying by 2 gives b+c
2
yields b + c + 2a = 318. (2)
When the average of her first and third marks is averaged with her second test mark, the new
a+c
+b
average is 81.5 so 2 2 = 81.5. Multiplying by 2 gives a+c
+ b = 163. Multiplying by 2 again
2
yields a + c + 2b = 326. (3)
By adding equations (1), (2) and (3) we obtain 4a + 4b + 4c = 988 which simplifies to
a + b + c = 247 after dividing by 4. This means that the sum of her first three marks is 247.
= 85. Substituting a + b + c = 247 we obtain
To obtain an average of 85% Ann needs a+b+c+d
4
247+d
= 85. Multiplying by 4 gives 247 + d = 340 or d = 93.
4
∴ to obtain an average of 85% Ann needs 93 on tomorrow’s test.
It would be a straight forward process to determine Ann’s first three test marks but our quest
did not ask us to do this. However, for the curious, on her first test Ann got 71, on her second
test Ann got 79, and on her third test Ann got 97.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
How Does This Function Function?
The function f (x) = x5 − 2x4 + ax3 − x2 + bx − 2 has a value of −7 when
x = −1.
Determine the value of the function when x = 1.
!"
$"
!#
%%
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
How Does This Function Function?
Problem
The function f (x) = x5 − 2x4 + ax3 − x2 + bx − 2 has a value of −7 when
x = −1. Determine the value of the function when x = 1.
Solution
We know that the function has a value of −7 when x = −1. Therefore,
f (−1) = −7.
f (−1)
(−1)5 − 2(−1)4 + a(−1)3 − (−1)2 + b(−1) − 2
−1 − 2 − a − 1 − b − 2
−a − b
∴a+b
=
=
=
=
=
−7
−7
−7
−1
1
(1)
At this point we seem to have used up the given information. Maybe we can
learn more by looking at precisely what we are asked to determine.
In this problem, we want the value of the function when x = 1. In other words,
we want f (1).
f (1) = 15 − 2(1)4 + a(1)3 − 12 + b(1) − 2
= 1−2+a−1+b−2
= a+b−4
But from (1) above, a + b = 1 so f (1) = (a + b) − 4 = (1) − 4 = −3.
Therefore, the value of the function is −3 when x = 1.
We are not given enough information to find the precise values of a and b but
enough information is given to solve the problem.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
An Uphill Battle
Lisa-Mai Winn and Will Race are training for a competition by running all the
way up and down a 700 m long ski slope. They each run up the slope at
different constant speeds. Coming down the slope, each runs at double her or
his uphill speed. Lisa-Mai reaches the top first, and immediately starts running
back down, meeting Will 70 m from the top.
When Lisa-Mai reaches the bottom, how far behind is Will?
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
An Uphill Battle
Problem
Lisa-Mai Winn and Will Race are training for a competition by running all the
way up and down a 700 m long ski slope. They each run up the slope at
different constant speeds. Coming down the slope, each runs at double her or
his uphill speed. Lisa-Mai reaches the top first, and immediately starts running
back down, meeting Will 70 m from the top. When Lisa-Mai reaches the
bottom, how far behind is Will?
Solution
Let a represent Lisa-Mai’s uphill speed and 2a represent her downhill speed.
Let b represent Will’s uphill speed and 2b represent his downhill speed.
We know that distance = speed × time or time = distance ÷ speed.
When Lisa and Will meet 70 m from the top of the hill, their times are the
same. At this time Will has run 700 − 70 = 630 m uphill.
Lisa’s Time Up 700 m + Lisa’s Time Down 70 m = Will’s Time Up 630 m
Reducing the second fraction:
Simplifying:
By rearranging, we obtain
a 735 7
=
= .
b
630 6
700 70
630
+
=
a
2a
b
630
700 35
+
=
a
a
b
735
630
=
a
b
(1)
Solution continues on the next page.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Let x represent the distance Will is behind Lisa at the end of the run.
When Lisa reaches the bottom, she has travelled 700 m up at a speed of a and
700 m down at a speed of 2a. Will has travelled 700 m up at a speed of b and
(700 − x) m down at a speed of 2b.
When Lisa reaches the bottom and Will is x m from the bottom, their times
are the same.
700 700
+
a
2a
1400 700
+
2a
2a
2100
2a
2100
Multiplying by 2,
a
It follows that
700 700 − x
+
b
2b
1400 700 − x
=
+
2b
2b
2100 − x
=
2b
2100 − x
=
b
=
a
2100
a 7
=
and = from (1) earlier.
b
2100 − x
b
6
∴
2100
7
=
2100 − x 6
Solving for x,
12600 = 14700 − 7x
7x = 2100
x = 300
Therefore Will Race is 300 m behind Lisa-Mai Winn when she
completes the run.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Playing With a Full Deck
R
S
T
Q
P
The diagram shows the plan for a deck which is to be built on the corner of a
cottage. A railing is to be constructed around the four outer edges of the deck
from P to Q to R to S to T . The length of the rail from P to Q is the same as
the length of the rail from S to T and the length of the rail from Q to R is the
same as the length of the rail from R to S. The total length of the railing is
30 m.
Determine the dimensions of the deck which will have the maximum area.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Playing With a Full Deck
Problem
The diagram shows the plan for a deck which is to be built
on the corner of a cottage. A railing is to be constructed
around the four outer edges of the deck from P to Q to
R to S to T . The length of the rail from P to Q is the same
as the length of the rail from S to T and the length of the
rail from Q to R is the same as the length of the rail from
R to S. The total length of the railing is 30 m. Determine
the dimensions of the deck which will have the maximum
area.
R
x
y
W y-x
S
x
y
V
Q
x
T
P
Solution
Label the corner of the cottage V . Draw a line segment through P V to RS intersecting at W .
P W ⊥ RS. This makes two rectangles P QRW and W ST V .
Let x represent the length of P Q and ST . Let y represent the length of QR and RS. Since
P QRW is a rectangle, RW = P Q = x and W S = RS − RW = y − x.
Let A represent the area of the deck.
The total length of fencing is P Q + QR + RS + ST = x + y + y + x = 2x + 2y = 30. By
dividing by 2, x + y = 15. Rearranging to solve for y we obtain y = 15 − x. (1)
Area of deck = Area P QRW + Area W ST V
A = QR × RW + W S × ST
= yx + (y − x)x
= (15 − x)x + ((15 − x) − x)x, substituting from (1) above
= (15 − x)x + (15 − 2x)x
= 15x − x2 + 15x − 2x2
= −3x2 + 30x
= −3(x2 − 10x)
= −3(x2 − 10x + 52 − 52 ), by completing the square
= −3(x − 5)2 + 75
This is the equation of a parabola which opens down from a vertex of (5, 75). The maximum
area is 75 m2 when x = 5 m. When x = 5, y = 15 − x = 15 − 5 = 10 m.
The side lengths of the deck are 5 m and 10 m giving a maximum area of 75 m2 .
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
What are the Chances of That?
Use each of the digits one to nine exactly once to form a nine digit number.
Determine the probability that the number formed is divisible by 4 or ends in 8.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
What are the Chances of That?
Problem
Use each of the digits one to nine exactly once to form a nine digit number. Determine the
probability that the number formed is divisible by 4 or ends in 8.
Solution
In creating a 9 digit number, there are 9 choices for the first digit, 8 choices for the second
digit, 7 choices for the third digit, and so on. So the number of 9 digit numbers is
9 × 8 × 7 × · · · × 2 × 1 = 9! = 362 880.
If the nine digit number ends in 8, there is only choice for the unit’s digit. There are then 8!
ways to create the remaining 8 digit number. Thus, the number of 9 digit numbers ending in 8
is 1 × 8! = 40 320.
For a number to be divisible by 4, the last two digits of the number must be divisible by 4.
There are 24 numbers less than 100 that are divisible by 4. This group includes 2 single digit
numbers, 4 and 8, which must be excluded. It also includes 4 two digit numbers ending in zero,
20, 40, 60 and 80. Zero is not one of the nine possible digits so these numbers must be
excluded. And finally the list includes 2 numbers, 44 and 88, which have repeated digits. Since
each digit can be used only once, these numbers must be excluded. Therefore, there are
24 − 2 − 4 − 2 or 16 valid two digit numbers which are divisible by 4. There are then 7! ways to
create the remaining 7 digit number. So the number of 9 digit numbers divisible by 4 is 16 × 7!
= 80 640.
If we added the 1 × 8! and the 16 × 7! we would be double counting the number of nine digit
numbers which end in 8 and are divisible by 4. So we must subtract off the number of numbers
which are divisible by 4 and end in 8 since they have been counted twice. There are 3 two digit
numbers with distinct digits, 28, 48, and 68, that end in 8 and are divisible by 4. As before,
there are 7! ways to create the remaining 7 digit number. So the number of 9 digit numbers
with distinct digits ending in 8 and divisible by 4 is 3 × 7! = 15 120.
We can now compute the required probability as follows:
(# ending in 8) + (# divisible by 4) − (# ending in 8 and divisible by 4)
(# of 9 digit numbers)
=
1 × 8! + 16 × 7! − 3 × 7!
40 320 + 80 640 − 15 120
105 840
7
=
=
= .
362 880
362 880
362 880
24
7.
∴ the probability that a nine digit number is divisible by 4 or ends in 8 is 24
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Answer the Question Asked
It is given that (x + y)2 = 16, (y + z)2 = 36, and (x + z)2 = 81.
If x + y + z ≥ 1, determine the number of possible values for x + y + z.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Answer the Question Asked
Problem
It is given that (x + y)2 = 16, (y + z)2 = 36, and (x + z)2 = 81.
If x + y + z ≥ 1, determine the number of possible values for x + y + z.
Solution
Since (x + y)2 = 16, x + y = ±4. Since (y + z)2 = 36, y + z = ±6. And since
(x + z)2 = 81, x + z = ±9.
Now (x + y) + (y + z) + (x + z) = 2x + 2y + 2z = 2(x + y + z). This quantity is
two times the value of the quantity we are looking for.
The following chart summarizes all possible combinations of values for x + y,
y + z, and x + z and the resulting values of 2x + 2y + 2z and x + y + z. The
final column of the chart states a yes or no answer to whether the value of
x + y + z is ≥ 1.
x+y y+z x+z
4
6
9
4
6
−9
4
−6
9
4
−6
−9
−4
6
9
−4
6
−9
−4
−6
9
−4
−6
−9
2x + 2y + 2z
19
1
7
−11
11
−7
−1
−19
x+y+z
9.5
0.5
3.5
−5.5
5.5
−3.5
−0.5
−9.5
≥ 1?
(yes / no)
yes
no
yes
no
yes
no
no
no
Therefore there are three possible values of x + y + z such that x + y + z ≥ 1.
It should be noted that for each of the three possibilities, values for x, y, and z
which produce each value can be determined.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
The Quest For Ann Sirs?
Ann Sirs has already written three mathematics tests, worth 100 marks each.
The average of her marks on her first two tests is calculated and then averaged
with her third test mark giving an average of 86%. The average of her marks
on her second and third tests is calculated and then averaged with her first test
mark giving an average of 79.5%. The average of her marks on her first and
third tests is calculated and then averaged with her second test mark giving an
average of 81.5%.
Her fourth mathematics test is tomorrow and it is also out of 100. What mark
does Ann need on her test to achieve an overall average of 85% in her
mathematics course?
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
The Quest For Ann Sirs?
Problem
Ann Sirs has already written three mathematics tests, worth 100 marks each. The average of
her marks on her first two tests is calculated and then averaged with her third test mark giving
an average of 86%. The average of her marks on her second and third tests is calculated and
then averaged with her first test mark giving an average of 79.5%. The average of her marks on
her first and third tests is calculated and then averaged with her second test mark giving an
average of 81.5%. Her fourth mathematics test is tomorrow and it is also out of 100. What
mark does Ann need on her test to achieve an overall average of 85% in her mathematics
course?
Solution
Let a represent Ann’s first mark, b represent Ann’s second mark, c represent Ann’s third mark
and d represent Ann’s fourth mark.
When the average of her first and second marks is averaged with her third test mark, the new
a+b
+c
+ c = 172. Multiplying by 2 again
average is 86 so 2 2 = 86. Multiplying by 2 gives a+b
2
yields a + b + 2c = 344. (1)
When the average of her second and third marks is averaged with her first test mark, the new
b+c
+a
+ a = 159. Multiplying by 2 again
average is 79.5 so 2 2 = 79.5. Multiplying by 2 gives b+c
2
yields b + c + 2a = 318. (2)
When the average of her first and third marks is averaged with her second test mark, the new
a+c
+b
average is 81.5 so 2 2 = 81.5. Multiplying by 2 gives a+c
+ b = 163. Multiplying by 2 again
2
yields a + c + 2b = 326. (3)
By adding equations (1), (2) and (3) we obtain 4a + 4b + 4c = 988 which simplifies to
a + b + c = 247 after dividing by 4. This means that the sum of her first three marks is 247.
= 85. Substituting a + b + c = 247 we obtain
To obtain an average of 85% Ann needs a+b+c+d
4
247+d
= 85. Multiplying by 4 gives 247 + d = 340 or d = 93.
4
∴ to obtain an average of 85% Ann needs 93 on tomorrow’s test.
It would be a straight forward process to determine Ann’s first three test marks but our quest
did not ask us to do this. However, for the curious, on her first test Ann got 71, on her second
test Ann got 79, and on her third test Ann got 97.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Palindrome Possibilities
A palindrome is a word or phrase which reads the same frontwards and
backwards. “I prefer pi” is an excellent example of a palindrome phrase.
Numbers which remain the same when the digits are reversed are also
considered to be palindromes. For example, 1287821 and 4554 are palindromic
numbers.
Hannah and Habibah have a special interest in palindromic numbers.
Determine, for them, the probability that a five-digit integer greater than or
equal to 10 000 is a palindrome.
!"#$%&'()%*#+
!"#$%&'()%*#+
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Palindrome Possibilities
Problem
A palindrome is a word or phrase which reads the same frontwards and backwards. “I prefer
pi” is an excellent example of a palindrome phrase. Numbers which remain the same when the
digits are reversed are also considered to be palindromes. For example, 1287821 and 4554 are
palindromic numbers. Hannah and Habibah have a special interest in palindromic numbers.
Determine, for them, the probability that a five-digit integer greater than or equal to 10 000 is
a palindrome.
Solution
First we must determine how many five-digit numbers greater than or equal to 10 000 there
are. The largest five-digit number is 99 999 so there are 99 999 numbers from 1 to the largest
five-digit number. This includes the 9 999 numbers from 1 to 9 999 which must be excluded.
So the number of five-digit numbers is 99 999 − 9 999 = 90 000.
Now we can determine how many five-digit palindromes there are. These numbers look like
abcba. Once the first digit is selected, the last digit is known (and there is really no choice).
Once the second digit is chosen, the fourth digit is known (and again there is really no choice).
There are 9 choices for the first digit. Zero cannot be used as a first digit since the number
must be greater than or equal to 10 000.
For each of the 9 choices for the first digit, there are 10 choices for the second digit. Therefore,
there are 9 × 10 = 90 choices for the first two digits.
For each of the 90 choices for the first two digits, there are 10 choices for the third digit.
Therefore, there are 90 × 10 = 900 choices for the first three digits.
Once the first three digits are chosen there is exactly one choice for each of the fourth and fifth
digits. The fourth digit must be the same as the second digit and the fifth digit must be the
same as the first digit. This means that there are 900 × 1 × 1 = 900 five-digit palindromes
greater than or equal to 10 000.
The probability is calculated by dividing the number of five-digit palindromes greater than or
equal to 10 000 by the number of five-digit numbers greater than or equal to 10 000.
∴ the probability that a five digit number is a palindrome =
1
900
=
.
90 000
100
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
A Shady Space
A
L
K
B
C
M
4ABC is an equilateral triangle with sides of length 2 cm. ALB, BM C, and
CKA are arcs of circles having centres C, A, and B, respectively.
Determine the total area of the shaded regions in the diagram.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
A Shady Space
Problem
A
L
B
K
D
M
C
4ABC is an equilateral triangle with sides of length 2 cm. ALB, BM C, and CKA are arcs of
circles having centres C, A, and B, respectively. Determine the total area of the shaded regions
in the diagram.
Solution
First, determine the area of equilateral 4ABC. Construct the altitude AD. Since the triangle
is equilateral,
all angles are 60◦ . Therefore, 4ABD is a 30◦ , 60◦ , 90◦ triangle with sides in
√
ratio 1 : 3 : 2.
√
Since AB = 2, BD = 1, we get AD = 3, and
√
√
area 4ABC = (BC)(AD) ÷ 2 = (2)( 3) ÷ 2 = 3 cm2
Each sector ABM C, BCKA and CALB has the same radius, 2 cm, and a 60◦ central angle.
Therefore each sector has the same area, 60 ÷ 360 or one-sixth the area of a circle of radius 2
cm.
area ABM C =
2
1 2 1
πr = π(2)2 = π cm2
6
6
3
The shaded part of each sector is equal to the area of the sector minus the area of the
equilateral 4ABC.
∴ Total Shaded Area = 3(area of any whole sector - area of the equilateral triangle)
= 3(area of sector ABM C − area 4ABC)
√
2
= 3
π− 3
3
√
= (2π − 3 3) cm2
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
More Power
When n = 62011 is expressed as an integer, what are its last two digits?
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
More Power
Problem
When n = 62011 is expressed as an integer, what are its last two digits?
Solution
Start by examining the last two digits of various powers of 6.
61 = 06
62 = 36
63 = 216
64 = 1 296
65 = 7 776
66 = 46 656
67 = 279 936
68 = 1 679 616
69 = 10 077 696
610 = 60 466 176
611 = 362 797 056
Notice that the last two digits repeat every five powers of 6 starting with the
2nd power of 6. The pattern continues. 612 ends with 36, 613 ends with 16, 614
ends with 96, 615 ends with 76, 616 ends with 56, and so on. Starting with the
second power of 6, every five consecutive powers of 6 will have the last two
digits 36, 16, 96, 76, and 56.
We need to determine the number of complete cycles in 2011 by first
subtracting 1 to allow for 06 at the beginning of the list and then dividing
2011 − 1 or 2010 by 5.
2010
= 402
5
So there are 402 complete cycles through the digit pattern to get to 62011 .
Since 62011 is the last number in the pattern it ends in 56.
Therefore 62011 ends with the digits 56.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
What’s Your Angle?
E
A
C
B
F
A is the centre of a circle which passes through B. B is the centre of a circle
which passes through A. CAE and CBF are straight line segments.
If ∠F = 78◦ , determine the measure of ∠C.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
What’s Your Angle?
Problem
E
x
A is the centre of a circle which passes through B.
B is the centre of a circle which passes through
A. CAE and CBF are straight line segments. If
∠F = 78◦ , determine the measure of ∠C.
A
y
C
x
y
78
B
Solution
Construct AB and BE. A, E and F are on the circumference of the circle with
centre B. Therefore, BA = BE = BF .
In 4BEF , BE = BF . Then 4BEF is isosceles and ∠BEF = ∠F = 78◦ .
Let x = ∠BEA and y = ∠ABC.
In 4BAE, BA = BE and the triangle is isosceles. Therefore,
∠BAE = ∠BEA = x.
Since B and C are on the circle with centre A, AC = AB and 4ABC is
isosceles. Therefore, ∠C = ∠ABC = y.
∠EAB is an exterior angle to 4ABC. By the exterior angle theorem for
triangles, ∠EAB = ∠C + ∠ABC. But ∠EAB = x and
∠C + ∠ABC = y + y = 2y. Therefore, x = 2y.
In 4CEF ,
∠C + ∠E + ∠F = 180◦
∠C + ∠CEB + ∠BEF + 78◦ = 180◦
y + x + 78◦ + 78◦ = 180◦
But x = 2y,
∴ y + 2y + 156◦ = 180◦
3y = 24◦
y = 8◦
Therefore, ∠C = 8◦ .
F
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Answer the Question Asked
It is given that (x + y)2 = 16, (y + z)2 = 36, and (x + z)2 = 81.
If x + y + z ≥ 1, determine the number of possible values for x + y + z.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Answer the Question Asked
Problem
It is given that (x + y)2 = 16, (y + z)2 = 36, and (x + z)2 = 81.
If x + y + z ≥ 1, determine the number of possible values for x + y + z.
Solution
Since (x + y)2 = 16, x + y = ±4. Since (y + z)2 = 36, y + z = ±6. And since
(x + z)2 = 81, x + z = ±9.
Now (x + y) + (y + z) + (x + z) = 2x + 2y + 2z = 2(x + y + z). This quantity is
two times the value of the quantity we are looking for.
The following chart summarizes all possible combinations of values for x + y,
y + z, and x + z and the resulting values of 2x + 2y + 2z and x + y + z. The
final column of the chart states a yes or no answer to whether the value of
x + y + z is ≥ 1.
x+y y+z x+z
4
6
9
4
6
−9
4
−6
9
4
−6
−9
−4
6
9
−4
6
−9
−4
−6
9
−4
−6
−9
2x + 2y + 2z
19
1
7
−11
11
−7
−1
−19
x+y+z
9.5
0.5
3.5
−5.5
5.5
−3.5
−0.5
−9.5
≥ 1?
(yes / no)
yes
no
yes
no
yes
no
no
no
Therefore there are three possible values of x + y + z such that x + y + z ≥ 1.
It should be noted that for each of the three possibilities, values for x, y, and z
which produce each value can be determined.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Love is in the Air
In Mr. Vee’s Physics class, each student gave every other student a valentine.
Mr. Vee did not give or receive any valentines. The girls received a total of 540
valentines and the boys received a total of 390 valentines.
How many students are in Mr. Vee’s class? How many girls are in the class?
How many boys are in the class?
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Love is in the Air
Problem
In Mr. Vee’s Physics class, each student gave every
other student a valentine. Mr. Vee did not give or
receive any valentines. The girls received a total of
540 valentines and the boys received a total of 390
valentines. How many students are in Mr. Vee’s
class? How many girls are in the class? How many
boys are in the class?
Solution
Let n represent the number of students in Mr. Vee’s class.
Each student sends n − 1 valentines and the total number of valentines sent is
540 + 390 or 930 valentines. So the number of students, n, times the number of
valentines sent, n − 1, equals the total number of valentines.
n(n − 1) = 930
n2 − n − 930 = 0
(n − 31)(n + 30) = 0
n = 31 or n = −30 but n > 0, ∴ n = 31
Therefore, there are 31 students in the class and each student sent 30
valentines and received 30 valentines.
Since the girls received a total of 540 valentines and each student received 30
valentines, there are 540 ÷ 30 or 18 girls in the class.
Since the boys received a total of 390 valentines and each student received 30
valentines, there are 390 ÷ 30 or 13 boys in the class.
Mr. Vee’s class has 31 students, 18 girls and 13 boys.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
How Many Children Are There Anyway?
A man died leaving some money in his estate. All of this money was to be
divided among his children in the following manner:
$x to the first born plus
1
16
of what remains, then
$2x to the second born plus
$3x to the third born plus
1
16
1
16
of what then remains, then
of what then remains, and so on.
When the distribution of the money was complete, each child received the
same amount and no money was left over. Determine the number of children.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
How Many Children Are There Anyway?
Problem
A man died leaving some money in his estate. All of this money was to be divided among his
1
children in the following manner: $x to the first born plus 16
of what remains, $2x to the
1
1
of what then remains,
second born plus 16 of what then remains, $3x to the third born plus 16
and so on. When the distribution of the money was complete, each child received the same
amount and no money was left over. Determine the number of children.
Solution
Let T be the total value of the estate. T > 0 since there is money in the estate.
Let y be the amount of money given to each child. y > 0 since each child receives money.
Then Ty is the number of children.
The first child receives x to begin with. There would be (T − x) left at this point. The first
1
child then receives 16
of the remaining amount (T − x). Therefore, the first child receives
1
(T − x).
y = x + 16
The second child receives 2x to begin with. There would now be (T − y − 2x) left in the estate.
This represents the original amount minus the first child’s full share minus the amount received
1
of the remaining amount
so far by the second child. The second child then receives 16
1
(T − y − 2x). Therefore, the second child receives y = 2x + 16 (T − y − 2x).
But each child receives the same amount.
1
1
∴ x + (T − x) = 2x + (T − y − 2x)
16
16
1
1
1
1
1
x + T − x = 2x + T − y − (2x)
16
16
16
16
16
1
1
2
x − x = 2x − y − x
16
16
16
Multiply each side of the equation by 16.
16x − x = 32x − y − 2x
15x = 30x − y
y = 15x
Therefore each child receives $15x.
(The solution continues on the next page.)
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Substituting 15x for y into the equation y = x +
x+
1
(T
16
− x) we obtain
1
(T − x) = 15x
16
1
(T − x) = 14x
16
T − x = 224x
T = 225x
Therefore the total value of the estate is 225x.
We can now determine the number of children
T
y
=
225x
15x
= 15.
Therefore the father had 15 children.
Notice, we did not need to know T , the total value of the estate. It turns out that once we
know x, we can determine each child’s share, 15x, and the total value of the estate, T = 225x.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
A Problem For The Ages
A four-digit number which is a perfect square is created by writing Jennifer’s
age in years followed by John’s age in years. Similarly, in 31 years, their ages in
the same order will again form a four-digit perfect square.
How old are Jennifer and John today?
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
A Problem For The Ages
Problem
A four-digit number which is a perfect square is created by writing Jennifer’s age in years
followed by John’s age in years. Similarly, in 31 years, their ages in the same order will again
form a four-digit perfect square. How old are Jennifer and John today?
Solution
Both Jennifer’s age and John’s age must be two digit numbers. If Jennifer’s age is a one-digit
number, John’s age would have to be a three-digit number to create the four-digit perfect
square. But in 31 years, Jennifer’s age would then be a two-digit number resulting in at least a
five-digit number when their ages are used to form the second perfect square. A similar
argument could be presented if John’s age is a one-digit number. Therefore, both Jennifer and
John have ages that are each two-digit numbers.
Let Jennifer’s present age be x and John’s present age be y. Then 100x + y is the four digit
number created by writing Jennifer’s age followed by John’s age. But 100x + y is a perfect
square so let 100x + y = k 2 , for some positive integer k.
In 31 years, Jennifer will be (x + 31) and John will be (y + 31). The new number created by
writing Jennifer’s age followed by John’s age is 100(x + 31) + (y + 31). This new four-digit
number is also a perfect square. So 100(x + 31) + (y + 31) = m2 , for some positive integer
m, m > k. This simplifies as follows:
100x + 3100 + y + 31 = m2
100x + y + 3131 = m2 (1)
From our work above, we also have 100x + y = k 2 . Substituting this into (1) we get
k 2 + 3131 = m2 or 3131 = m2 − k 2 . m2 − k 2 is a difference of squares, so
m2 − k 2 = (m + k)(m − k) = 3131.
Since m and k are positive integers, m + k is positive and m + k > m − k. m − k must also be
positive since (m + k)(m − k) = 3131. So we are looking for two positive numbers that
multiply to 3131. There are two possibilities, 3131 × 1 or 101 × 31.
First we will examine (m + k)(m − k) = 3131 × 1. From this we obtain two equations in two
unknowns, namely m + k = 3131 and m − k = 1. Subtracting the two equations gives
2k = 3130 or k = 1565. Then k 2 = 15652 = 2449225. This is not a four-digit number so
3131 × 1 is not an admissible factorization of 3131.
Next we examine (m + k)(m − k) = 101 × 31. This leads to m + k = 101 and m − k = 31.
Subtracting the two equations we get 2k = 70 or k = 35. Then 100x + y = k 2 = 1225.
Therefore, x = 12 and y = 25 since 1225 is the four-digit number formed by writing Jennifer’s
age, x, followed by John’s age, y.
∴ today Jennifer is 12 and John is 25.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Trapped!
A four-sided figure with one pair of parallel sides is called a trapezoid. An
isosceles trapezoid is one in which the non-parallel sides are equal in length.
D
A
x
x
O
B
C
Isosceles trapezoid ABCD has parallel sides AD and BC and sides
AB = DC = x. The area of the trapezoid is 510 cm2 . A circle with centre O
and radius 10 cm is contained inside the trapezoid so that it is tangent to each
of the four sides of the trapezoid.
Determine the length of x.
For purposes of this problem accept the fact that a line drawn from the centre
of a circle to a point of tangency is perpendicular to the tangent.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Trapped!
Problem
Isosceles trapezoid ABCD has parallel sides AD and BC and sides
AB = DC = x. The area of the trapezoid is 510 cm2 . A circle with centre O
and radius 10 cm is contained inside the trapezoid so that it is tangent to each
of the four sides of the trapezoid. Determine the length of x.
For purposes of this problem accept the fact that a line drawn from the centre
of a circle to a point of tangency is perpendicular to the tangent.
Solution
Draw radii OP, OQ, OR, and OS to sides AB, BC, CD, and DA,
respectively. Then OP = OQ = OR = OS = 10 since they are each radii of the
circle. Also, since each line drawn from the centre of the circle to a point of
tangency is perpendicular to the tangent,
∠OP A = ∠OQB = ∠ORD = ∠OSA = 90◦ .
Let AP = a and DR = b. Therefore, P B = x − a and RC = x − b. The
following diagram shows all of the given and found information.
A
S
a
D
b
P
R
x
x
x-a
B
O
Q
x-b
C
Join A to O forming two right triangles, 4AP O and 4ASO. Using the
Pythagorean Theorem, AP 2 = AO2 − OP 2 and AS 2 = AO2 − OS 2 . But
OP = OS since they are both radii. So the two expressions are equal and
AS = AP = a follows.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Using exactly the same reasoning that was used to show AP = AS = a, we can
show DR = DS = b, BP = BQ = x − a and CR = CQ = x − b. This new
information has been added to the diagram below.
A
a
S
b
a
D
b
P
R
x
x
O
x-a
B
x-a
Q
x-b
x-b
C
We can now find the area of the trapezoid. To find the area of a trapezoid, we
multiply the perpendicular distance between the two parallel sides by the sum
of the lengths of the two parallel sides and then divide the result by 2.
Area Trapezoid ABCD
510
510
510
510
25.5
=
=
=
=
=
=
SQ × (AD + BC) ÷ 2
(SO + OQ) × ((AS + SD) + (BQ + QC)) ÷ 2
(10 + 10) × ((a + b) + (x − a + x − b)) ÷ 2
(20) × (2x) ÷ 2
20x
x
Therefore, the length of x is 25.5 cm.
At the end of the statement of the problem, the following fact was assumed:
a line drawn f rom the centre of a circle to a point of tangency is
perpendicular to the tangent. As an extension to this problem the solver may
wish to try to prove this fact.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
How Does This Function Function?
The function f (x) = x5 − 2x4 + ax3 − x2 + bx − 2 has a value of −7 when
x = −1.
Determine the value of the function when x = 1.
!"
$"
!#
%%
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
How Does This Function Function?
Problem
The function f (x) = x5 − 2x4 + ax3 − x2 + bx − 2 has a value of −7 when
x = −1. Determine the value of the function when x = 1.
Solution
We know that the function has a value of −7 when x = −1. Therefore,
f (−1) = −7.
f (−1)
(−1)5 − 2(−1)4 + a(−1)3 − (−1)2 + b(−1) − 2
−1 − 2 − a − 1 − b − 2
−a − b
∴a+b
=
=
=
=
=
−7
−7
−7
−1
1
(1)
At this point we seem to have used up the given information. Maybe we can
learn more by looking at precisely what we are asked to determine.
In this problem, we want the value of the function when x = 1. In other words,
we want f (1).
f (1) = 15 − 2(1)4 + a(1)3 − 12 + b(1) − 2
= 1−2+a−1+b−2
= a+b−4
But from (1) above, a + b = 1 so f (1) = (a + b) − 4 = (1) − 4 = −3.
Therefore, the value of the function is −3 when x = 1.
We are not given enough information to find the precise values of a and b but
enough information is given to solve the problem.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
An Uphill Battle
Lisa-Mai Winn and Will Race are training for a competition by running all the
way up and down a 700 m long ski slope. They each run up the slope at
different constant speeds. Coming down the slope, each runs at double her or
his uphill speed. Lisa-Mai reaches the top first, and immediately starts running
back down, meeting Will 70 m from the top.
When Lisa-Mai reaches the bottom, how far behind is Will?
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
An Uphill Battle
Problem
Lisa-Mai Winn and Will Race are training for a competition by running all the
way up and down a 700 m long ski slope. They each run up the slope at
different constant speeds. Coming down the slope, each runs at double her or
his uphill speed. Lisa-Mai reaches the top first, and immediately starts running
back down, meeting Will 70 m from the top. When Lisa-Mai reaches the
bottom, how far behind is Will?
Solution
Let a represent Lisa-Mai’s uphill speed and 2a represent her downhill speed.
Let b represent Will’s uphill speed and 2b represent his downhill speed.
We know that distance = speed × time or time = distance ÷ speed.
When Lisa and Will meet 70 m from the top of the hill, their times are the
same. At this time Will has run 700 − 70 = 630 m uphill.
Lisa’s Time Up 700 m + Lisa’s Time Down 70 m = Will’s Time Up 630 m
Reducing the second fraction:
Simplifying:
By rearranging, we obtain
a 735 7
=
= .
b
630 6
700 70
630
+
=
a
2a
b
630
700 35
+
=
a
a
b
735
630
=
a
b
(1)
Solution continues on the next page.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Let x represent the distance Will is behind Lisa at the end of the run.
When Lisa reaches the bottom, she has travelled 700 m up at a speed of a and
700 m down at a speed of 2a. Will has travelled 700 m up at a speed of b and
(700 − x) m down at a speed of 2b.
When Lisa reaches the bottom and Will is x m from the bottom, their times
are the same.
700 700
+
a
2a
1400 700
+
2a
2a
2100
2a
2100
Multiplying by 2,
a
It follows that
700 700 − x
+
b
2b
1400 700 − x
=
+
2b
2b
2100 − x
=
2b
2100 − x
=
b
=
a
2100
a 7
=
and = from (1) earlier.
b
2100 − x
b
6
∴
2100
7
=
2100 − x 6
Solving for x,
12600 = 14700 − 7x
7x = 2100
x = 300
Therefore Will Race is 300 m behind Lisa-Mai Winn when she
completes the run.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Cutting Corners
A cube with side lengths 4 cm is to be cut in the following manner: the corner
of the cube is removed by making a cut through the midpoints of three
adjacent sides. The diagram shows the resulting figure after the first cut.
Similar cuts are made at each of the remaining corners of the cube.
Determine the increase or decrease in total surface area as a result of slicing
the eight corners off the original cube.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Cutting Corners
Problem
A cube with side lengths 4 cm is to be cut in the following manner:
the corner of the cube is removed by making a cut through the
midpoints of three adjacent sides. The diagram shows the resulting
figure after the first cut. Similar cuts are made at each of the
remaining corners of the cube. Determine the increase or decrease
in total surface area as a result of slicing the eight corners off the
original cube.
Solution
To determine the increase or decrease in surface area, we need only
look at one corner, find the surface area increase or decrease there
and multiply the result by eight to account for the eight corners.
At each corner, the surface area of three right angled triangles is
removed and replaced by the surface area of a single triangle.
Since the cut is made from the midpoints of three adjacent sides,
each right triangle has base and height with length 2 cm. The
resulting area of one of the right triangles is 12 (2)(2) = 2 cm2 .
The hypotenuse
of the right triangle is found using Pythagoras’ Thep
√
√
2
2
orem, 2 + 2 = 8 = 2 2. Since the length of the hypotenuse is
the same in each of the three right triangles, √
the remaining triangle
in the corner is equilateral with side lengths 2 2. The triangle looks
like the bottom triangle shown to the right.
The altitude of an equilateral triangle right bisects the base. Let
h be the
Theorem,
√
√ height
√ of the triangle. Using Pythagoras’
h2 = (2 2)2 − ( 2)2 = 8 − 2 = 6. Therefore h = 6.
√ √
√
√
The area of the remaining triangle is 12 (2 2)( 6) = 12 = 2 3.
2 2
h
2
2 2
2
In each corner, the new surface area is the area of the √
equilateral triangle
√ minus the area
√ of the
three right triangles. ∴ the remaining corner area is 2 3 − 3 × (2) = 2 3 − 6. Since 2 3 < 6,
this result is negative and
√ the surface area is decreased in each corner. Therefore the surface
area is reduced by 6 − 2 3 in each corner.
Since there√are eight corners,
√ . the total2decrease in surface area is
8 × (6 − 2 3) = 48 − 16 3 = 20.3 cm .
Therefore,
of cutting off each of the corners, the total surface area decreases by
√ as a result
2
(48 − 16 3) cm .
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
A Touchy Triangle
C
D
A
O
P
B
Two circles with centres O and P , each with a radius of 2, are tangent to each
other. A straight line is drawn through O and P meeting the circles at A
and B. Two other sides of 4ABC are drawn such that side AC is tangent to
the circle with centre P at D and side CB is tangent to the circle with
centre P at B.
Determine the length of BC.
For purposes of this problem accept the fact that a line drawn from the centre
of a circle to a point of tangency is perpendicular to the tangent.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
A Touchy Triangle
Problem
C
Two circles with centres O and P , each with a radius
of 2, are tangent to each other. A straight line is drawn
through O and P meeting the circles at A and B. Two
other sides of 4ABC are drawn such that side AC is
tangent to the circle with centre P at D and side CB
is tangent to the circle with centre P at B. Determine
the length of BC.
D
2
A
2 O
2T
2
P
Solution
Let T be the point of tangency of the two circles. Then
AO = OT = T P = P B = 2. Since AC is tangent to the circle with centre P
at D, CD ⊥ P D. Since CB is tangent to the circle with centre P at B,
CB ⊥ P B. Since P D and P B are radii of the circle with centre P ,
P D = P B = 2. This information has been added to the diagram.
4ADP is right angled at D since AD ⊥ P D. So
√
√
AD2 = AP 2 − P D2 = 62 − 22 = 36 − 4 = 32. Since AD > 0, AD = 32 = 4 2.
At this point there are many ways to find the length of CB. An interesting
(and possibly different) way to find CB is to use basic trigonometry in the
D
and in 4ACB, tan(A) = CB
right triangles. In 4AP D, tan(A) = PAD
AB .
PD
CB
=
AD
AB
2
CB
√ =
8
4 2
√
√
4
4 2
16
=2 2
CB = √ = √ =
2
4 2
2
√
Therefore the length of CB is 2 2.
∴
There are many other solutions to this problem. The solver can use
Pythagoras’ Theorem in 4ABC. Another solution uses similar triangles
4AP D and 4ACB.
B
2
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Playing With a Full Deck
R
S
T
Q
P
The diagram shows the plan for a deck which is to be built on the corner of a
cottage. A railing is to be constructed around the four outer edges of the deck
from P to Q to R to S to T . The length of the rail from P to Q is the same as
the length of the rail from S to T and the length of the rail from Q to R is the
same as the length of the rail from R to S. The total length of the railing is
30 m.
Determine the dimensions of the deck which will have the maximum area.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Playing With a Full Deck
Problem
The diagram shows the plan for a deck which is to be built
on the corner of a cottage. A railing is to be constructed
around the four outer edges of the deck from P to Q to
R to S to T . The length of the rail from P to Q is the same
as the length of the rail from S to T and the length of the
rail from Q to R is the same as the length of the rail from
R to S. The total length of the railing is 30 m. Determine
the dimensions of the deck which will have the maximum
area.
R
x
y
W y-x
S
x
y
V
Q
x
T
P
Solution
Label the corner of the cottage V . Draw a line segment through P V to RS intersecting at W .
P W ⊥ RS. This makes two rectangles P QRW and W ST V .
Let x represent the length of P Q and ST . Let y represent the length of QR and RS. Since
P QRW is a rectangle, RW = P Q = x and W S = RS − RW = y − x.
Let A represent the area of the deck.
The total length of fencing is P Q + QR + RS + ST = x + y + y + x = 2x + 2y = 30. By
dividing by 2, x + y = 15. Rearranging to solve for y we obtain y = 15 − x. (1)
Area of deck = Area P QRW + Area W ST V
A = QR × RW + W S × ST
= yx + (y − x)x
= (15 − x)x + ((15 − x) − x)x, substituting from (1) above
= (15 − x)x + (15 − 2x)x
= 15x − x2 + 15x − 2x2
= −3x2 + 30x
= −3(x2 − 10x)
= −3(x2 − 10x + 52 − 52 ), by completing the square
= −3(x − 5)2 + 75
This is the equation of a parabola which opens down from a vertex of (5, 75). The maximum
area is 75 m2 when x = 5 m. When x = 5, y = 15 − x = 15 − 5 = 10 m.
The side lengths of the deck are 5 m and 10 m giving a maximum area of 75 m2 .
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
A Shady Space
A
L
K
B
C
M
4ABC is an equilateral triangle with sides of length 2 cm. ALB, BM C, and
CKA are arcs of circles having centres C, A, and B, respectively.
Determine the total area of the shaded regions in the diagram.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
A Shady Space
Problem
A
L
B
K
D
M
C
4ABC is an equilateral triangle with sides of length 2 cm. ALB, BM C, and CKA are arcs of
circles having centres C, A, and B, respectively. Determine the total area of the shaded regions
in the diagram.
Solution
First, determine the area of equilateral 4ABC. Construct the altitude AD. Since the triangle
is equilateral,
all angles are 60◦ . Therefore, 4ABD is a 30◦ , 60◦ , 90◦ triangle with sides in
√
ratio 1 : 3 : 2.
√
Since AB = 2, BD = 1, we get AD = 3, and
√
√
area 4ABC = (BC)(AD) ÷ 2 = (2)( 3) ÷ 2 = 3 cm2
Each sector ABM C, BCKA and CALB has the same radius, 2 cm, and a 60◦ central angle.
Therefore each sector has the same area, 60 ÷ 360 or one-sixth the area of a circle of radius 2
cm.
area ABM C =
2
1 2 1
πr = π(2)2 = π cm2
6
6
3
The shaded part of each sector is equal to the area of the sector minus the area of the
equilateral 4ABC.
∴ Total Shaded Area = 3(area of any whole sector - area of the equilateral triangle)
= 3(area of sector ABM C − area 4ABC)
√
2
= 3
π− 3
3
√
= (2π − 3 3) cm2
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Trapped!
A four-sided figure with one pair of parallel sides is called a trapezoid. An
isosceles trapezoid is one in which the non-parallel sides are equal in length.
D
A
x
x
O
B
C
Isosceles trapezoid ABCD has parallel sides AD and BC and sides
AB = DC = x. The area of the trapezoid is 510 cm2 . A circle with centre O
and radius 10 cm is contained inside the trapezoid so that it is tangent to each
of the four sides of the trapezoid.
Determine the length of x.
For purposes of this problem accept the fact that a line drawn from the centre
of a circle to a point of tangency is perpendicular to the tangent.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Trapped!
Problem
Isosceles trapezoid ABCD has parallel sides AD and BC and sides
AB = DC = x. The area of the trapezoid is 510 cm2 . A circle with centre O
and radius 10 cm is contained inside the trapezoid so that it is tangent to each
of the four sides of the trapezoid. Determine the length of x.
For purposes of this problem accept the fact that a line drawn from the centre
of a circle to a point of tangency is perpendicular to the tangent.
Solution
Draw radii OP, OQ, OR, and OS to sides AB, BC, CD, and DA,
respectively. Then OP = OQ = OR = OS = 10 since they are each radii of the
circle. Also, since each line drawn from the centre of the circle to a point of
tangency is perpendicular to the tangent,
∠OP A = ∠OQB = ∠ORD = ∠OSA = 90◦ .
Let AP = a and DR = b. Therefore, P B = x − a and RC = x − b. The
following diagram shows all of the given and found information.
A
S
a
D
b
P
R
x
x
x-a
B
O
Q
x-b
C
Join A to O forming two right triangles, 4AP O and 4ASO. Using the
Pythagorean Theorem, AP 2 = AO2 − OP 2 and AS 2 = AO2 − OS 2 . But
OP = OS since they are both radii. So the two expressions are equal and
AS = AP = a follows.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Using exactly the same reasoning that was used to show AP = AS = a, we can
show DR = DS = b, BP = BQ = x − a and CR = CQ = x − b. This new
information has been added to the diagram below.
A
a
S
b
a
D
b
P
R
x
x
O
x-a
B
x-a
Q
x-b
x-b
C
We can now find the area of the trapezoid. To find the area of a trapezoid, we
multiply the perpendicular distance between the two parallel sides by the sum
of the lengths of the two parallel sides and then divide the result by 2.
Area Trapezoid ABCD
510
510
510
510
25.5
=
=
=
=
=
=
SQ × (AD + BC) ÷ 2
(SO + OQ) × ((AS + SD) + (BQ + QC)) ÷ 2
(10 + 10) × ((a + b) + (x − a + x − b)) ÷ 2
(20) × (2x) ÷ 2
20x
x
Therefore, the length of x is 25.5 cm.
At the end of the statement of the problem, the following fact was assumed:
a line drawn f rom the centre of a circle to a point of tangency is
perpendicular to the tangent. As an extension to this problem the solver may
wish to try to prove this fact.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
An Uphill Battle
Lisa-Mai Winn and Will Race are training for a competition by running all the
way up and down a 700 m long ski slope. They each run up the slope at
different constant speeds. Coming down the slope, each runs at double her or
his uphill speed. Lisa-Mai reaches the top first, and immediately starts running
back down, meeting Will 70 m from the top.
When Lisa-Mai reaches the bottom, how far behind is Will?
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
An Uphill Battle
Problem
Lisa-Mai Winn and Will Race are training for a competition by running all the
way up and down a 700 m long ski slope. They each run up the slope at
different constant speeds. Coming down the slope, each runs at double her or
his uphill speed. Lisa-Mai reaches the top first, and immediately starts running
back down, meeting Will 70 m from the top. When Lisa-Mai reaches the
bottom, how far behind is Will?
Solution
Let a represent Lisa-Mai’s uphill speed and 2a represent her downhill speed.
Let b represent Will’s uphill speed and 2b represent his downhill speed.
We know that distance = speed × time or time = distance ÷ speed.
When Lisa and Will meet 70 m from the top of the hill, their times are the
same. At this time Will has run 700 − 70 = 630 m uphill.
Lisa’s Time Up 700 m + Lisa’s Time Down 70 m = Will’s Time Up 630 m
Reducing the second fraction:
Simplifying:
By rearranging, we obtain
a 735 7
=
= .
b
630 6
700 70
630
+
=
a
2a
b
630
700 35
+
=
a
a
b
735
630
=
a
b
(1)
Solution continues on the next page.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Let x represent the distance Will is behind Lisa at the end of the run.
When Lisa reaches the bottom, she has travelled 700 m up at a speed of a and
700 m down at a speed of 2a. Will has travelled 700 m up at a speed of b and
(700 − x) m down at a speed of 2b.
When Lisa reaches the bottom and Will is x m from the bottom, their times
are the same.
700 700
+
a
2a
1400 700
+
2a
2a
2100
2a
2100
Multiplying by 2,
a
It follows that
700 700 − x
+
b
2b
1400 700 − x
=
+
2b
2b
2100 − x
=
2b
2100 − x
=
b
=
a
2100
a 7
=
and = from (1) earlier.
b
2100 − x
b
6
∴
2100
7
=
2100 − x 6
Solving for x,
12600 = 14700 − 7x
7x = 2100
x = 300
Therefore Will Race is 300 m behind Lisa-Mai Winn when she
completes the run.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Cutting Corners
A cube with side lengths 4 cm is to be cut in the following manner: the corner
of the cube is removed by making a cut through the midpoints of three
adjacent sides. The diagram shows the resulting figure after the first cut.
Similar cuts are made at each of the remaining corners of the cube.
Determine the increase or decrease in total surface area as a result of slicing
the eight corners off the original cube.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Cutting Corners
Problem
A cube with side lengths 4 cm is to be cut in the following manner:
the corner of the cube is removed by making a cut through the
midpoints of three adjacent sides. The diagram shows the resulting
figure after the first cut. Similar cuts are made at each of the
remaining corners of the cube. Determine the increase or decrease
in total surface area as a result of slicing the eight corners off the
original cube.
Solution
To determine the increase or decrease in surface area, we need only
look at one corner, find the surface area increase or decrease there
and multiply the result by eight to account for the eight corners.
At each corner, the surface area of three right angled triangles is
removed and replaced by the surface area of a single triangle.
Since the cut is made from the midpoints of three adjacent sides,
each right triangle has base and height with length 2 cm. The
resulting area of one of the right triangles is 12 (2)(2) = 2 cm2 .
The hypotenuse
of the right triangle is found using Pythagoras’ Thep
√
√
2
2
orem, 2 + 2 = 8 = 2 2. Since the length of the hypotenuse is
the same in each of the three right triangles, √
the remaining triangle
in the corner is equilateral with side lengths 2 2. The triangle looks
like the bottom triangle shown to the right.
The altitude of an equilateral triangle right bisects the base. Let
h be the
Theorem,
√
√ height
√ of the triangle. Using Pythagoras’
h2 = (2 2)2 − ( 2)2 = 8 − 2 = 6. Therefore h = 6.
√ √
√
√
The area of the remaining triangle is 12 (2 2)( 6) = 12 = 2 3.
2 2
h
2
2 2
2
In each corner, the new surface area is the area of the √
equilateral triangle
√ minus the area
√ of the
three right triangles. ∴ the remaining corner area is 2 3 − 3 × (2) = 2 3 − 6. Since 2 3 < 6,
this result is negative and
√ the surface area is decreased in each corner. Therefore the surface
area is reduced by 6 − 2 3 in each corner.
Since there√are eight corners,
√ . the total2decrease in surface area is
8 × (6 − 2 3) = 48 − 16 3 = 20.3 cm .
Therefore,
of cutting off each of the corners, the total surface area decreases by
√ as a result
2
(48 − 16 3) cm .
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
A Touchy Triangle
C
D
A
O
P
B
Two circles with centres O and P , each with a radius of 2, are tangent to each
other. A straight line is drawn through O and P meeting the circles at A
and B. Two other sides of 4ABC are drawn such that side AC is tangent to
the circle with centre P at D and side CB is tangent to the circle with
centre P at B.
Determine the length of BC.
For purposes of this problem accept the fact that a line drawn from the centre
of a circle to a point of tangency is perpendicular to the tangent.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
A Touchy Triangle
Problem
C
Two circles with centres O and P , each with a radius
of 2, are tangent to each other. A straight line is drawn
through O and P meeting the circles at A and B. Two
other sides of 4ABC are drawn such that side AC is
tangent to the circle with centre P at D and side CB
is tangent to the circle with centre P at B. Determine
the length of BC.
D
2
A
2 O
2T
2
P
Solution
Let T be the point of tangency of the two circles. Then
AO = OT = T P = P B = 2. Since AC is tangent to the circle with centre P
at D, CD ⊥ P D. Since CB is tangent to the circle with centre P at B,
CB ⊥ P B. Since P D and P B are radii of the circle with centre P ,
P D = P B = 2. This information has been added to the diagram.
4ADP is right angled at D since AD ⊥ P D. So
√
√
AD2 = AP 2 − P D2 = 62 − 22 = 36 − 4 = 32. Since AD > 0, AD = 32 = 4 2.
At this point there are many ways to find the length of CB. An interesting
(and possibly different) way to find CB is to use basic trigonometry in the
D
and in 4ACB, tan(A) = CB
right triangles. In 4AP D, tan(A) = PAD
AB .
PD
CB
=
AD
AB
2
CB
√ =
8
4 2
√
√
4
4 2
16
=2 2
CB = √ = √ =
2
4 2
2
√
Therefore the length of CB is 2 2.
∴
There are many other solutions to this problem. The solver can use
Pythagoras’ Theorem in 4ABC. Another solution uses similar triangles
4AP D and 4ACB.
B
2
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Playing With a Full Deck
R
S
T
Q
P
The diagram shows the plan for a deck which is to be built on the corner of a
cottage. A railing is to be constructed around the four outer edges of the deck
from P to Q to R to S to T . The length of the rail from P to Q is the same as
the length of the rail from S to T and the length of the rail from Q to R is the
same as the length of the rail from R to S. The total length of the railing is
30 m.
Determine the dimensions of the deck which will have the maximum area.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Playing With a Full Deck
Problem
The diagram shows the plan for a deck which is to be built
on the corner of a cottage. A railing is to be constructed
around the four outer edges of the deck from P to Q to
R to S to T . The length of the rail from P to Q is the same
as the length of the rail from S to T and the length of the
rail from Q to R is the same as the length of the rail from
R to S. The total length of the railing is 30 m. Determine
the dimensions of the deck which will have the maximum
area.
R
x
y
W y-x
S
x
y
V
Q
x
T
P
Solution
Label the corner of the cottage V . Draw a line segment through P V to RS intersecting at W .
P W ⊥ RS. This makes two rectangles P QRW and W ST V .
Let x represent the length of P Q and ST . Let y represent the length of QR and RS. Since
P QRW is a rectangle, RW = P Q = x and W S = RS − RW = y − x.
Let A represent the area of the deck.
The total length of fencing is P Q + QR + RS + ST = x + y + y + x = 2x + 2y = 30. By
dividing by 2, x + y = 15. Rearranging to solve for y we obtain y = 15 − x. (1)
Area of deck = Area P QRW + Area W ST V
A = QR × RW + W S × ST
= yx + (y − x)x
= (15 − x)x + ((15 − x) − x)x, substituting from (1) above
= (15 − x)x + (15 − 2x)x
= 15x − x2 + 15x − 2x2
= −3x2 + 30x
= −3(x2 − 10x)
= −3(x2 − 10x + 52 − 52 ), by completing the square
= −3(x − 5)2 + 75
This is the equation of a parabola which opens down from a vertex of (5, 75). The maximum
area is 75 m2 when x = 5 m. When x = 5, y = 15 − x = 15 − 5 = 10 m.
The side lengths of the deck are 5 m and 10 m giving a maximum area of 75 m2 .
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Endless Possibilities?
The digits 1, 2, 3, 4, and 5 are each used once to create a five digit number
abcde which satisfies the following conditions:
(i) the three digit number abc is odd;
(ii) the three digit number bcd is divisible by 5; and
(iii) the three digit number cde is divisible by 3.
Determine every five digit number formed using each of the digits 1 to 5
exactly once that satisfies all three conditions.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Endless Possibilities?
Problem
The digits 1, 2, 3, 4, and 5 are each used once to create a five digit number
abcde which satisfies the following conditions: (i) the three digit number abc is
odd; (ii) the three digit number bcd is divisible by 5; and (iii) the three digit
number cde is divisible by 3. Determine every five digit number formed using
each of the digits 1 to 5 exactly once that satisfies all three conditions.
Solution
It turns out that the possibilities are really not endless. In fact, the
possibilities are quite limited.
In condition (ii), bcd is divisible by 5. For this to happen, d = 5 is the only
possibility. ∴ the number looks like abc5e.
Since, by condition (i), abc is odd, c must be an odd number and thus c must
be 1, 3 or 5. But each digit can be used only once so 5 is eliminated. ∴ the
number looks like ab15e or ab35e.
For a number to be divisible by 3, the sum of its digits must be divisible by 3.
In condition (iii), cde must be divisible by 3 so the sum c + d + e must be
divisible by 3.
In the number ab15e, cde = 15e and the only possible value for e such that 15e
is divisible by 3 is e = 3. So cde = 153.
In the number ab35e, cde = 35e and for 35e to be divisible by 3, e could be
either 1 or 4. So cde = 351 or cde = 354.
There are then only 3 possible values for the last three digits: 153, 351 or 354.
The remaining two digits can be placed in position a or b in either order. So
for each of the numbers 153, 351 and 354, there are two possible first digits
giving a total of 6 possible numbers that satisfy all three conditions: 24153,
42153, 24351, 42351, 12354, and 21354.
∴ the 6 numbers that satisfy all three conditions are 24153, 42153,
24351, 42351, 12354, and 21354.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E
Find the Number
Five different numbers, a, b, c, d, and e, are written in order smallest to largest
such that a < b < c < d < e. When the numbers are added in pairs the
following sums are obtained: 726, 756, 770, 781, 795, 816, 825, 830, 860 and 885.
Determine the sum of the five numbers and determine the value of the smallest
number, a.
!!
$
"!
$
#!
$
&! $
%!
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Problem of the Week
Problem E and Solution
Find the Number
Problem
Five different numbers, a, b, c, d, and e, are written in order smallest to largest
such that a < b < c < d < e. When the numbers are added in pairs the
following sums are obtained: 726, 756, 770, 781, 795, 816, 825, 830, 860 and 885.
Determine the sum of the five numbers and determine the value of the smallest
number, a.
Solution
We know the sum of each pair so we can determine the sum of all of the sums.
(a+b)+(a+c)+(a+d)+(a+e)+(b+c)+(b+d)+(b+e)+(c+d)+(c+e)+(d+e)
= 4a + 4b + 4c + 4d + 4e
= 726 + 756 + 770 + 781 + 795 + 816 + 825 + 830 + 860 + 885
= 8 044
Therefore 4a + 4b + 4c + 4d + 4e = 8 044. Dividing each side of the equation by
4, we obtain a + b + c + d + e = 2 011. That is, the sum of the five numbers is
2 011.
The smallest sum is created by adding the two smallest numbers. Therefore,
a + b = 726. The largest sum is created by adding the two largest numbers.
Therefore, d + e = 885. If we subtract the sum of the two smallest numbers
and the sum of the two largest numbers from the total sum, we will get the
middle number, c.
(a + b + c + d + e) − (a + b) − (d + e) = 2 011 − 726 − 885
∴ c = 400
The second smallest sum is created by adding the smallest number, a, to the
middle number, c. (A justification of this statement is shown on the next
page.) Therefore, a + c = 756 and a = 756 − c = 756 − 400 = 356.
The sum of the five numbers is 2 011 and the smallest number is 356. The
complete list is 356, 370, 400, 425 and 460. It is left as an exercise for the
student to verify the correctness of this list.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Why is a + c is the second smallest sum?
We know that a < b < c < d < e so the following is true:
1. Since b > a, let b = a + m, m > 0.
2. Since c > b, c = b + n = a + m + n, m, n > 0.
3. Since d > c, d = c + p = a + m + n + p, m, n, p > 0.
4. Since e > d, e = d + q = a + m + n + p + q, m, n, p, q > 0.
We need to show that a + c > a + b and a + c is smaller than all other possible sums. So now
let’s look at the ten possible sums:
1. a + b = a + a + m = 2a + m.
2. a + c = a + a + m + n = 2a + m + n > 2a + m = a + b.
So a + c > a + b.
3. a + d = a + a + m + n + p = 2a + m + n + p > 2a + m + n = a + c.
So a + d > a + c.
4. a + e = a + a + m + n + p + q = 2a + m + n + p + q > 2a + m + n = a + c.
So a + e > a + c.
5. b + c = a + m + a + m + n = 2a + 2m + n > 2a + m + n = a + c.
So b + c > a + c.
6. b + d = a + m + a + m + n + p = 2a + 2m + n + p > 2a + m + n = a + c.
So b + d > a + c.
7. b + e = a + m + a + m + n + p + q = 2a + 2m + n + p + q > 2a + m + n = a + c.
So b + e > a + c.
8. c + d = a + m + n + a + m + n + p = 2a + 2m + 2n + p > 2a + m + n = a + c.
So c + d > a + c.
9. c + e = a + m + n + a + m + n + p + q = 2a + 2m + 2n + p + q > 2a + m + n = a + c.
So c + e > a + c.
10. d + e = a + m + n + p + a + m + n + p + q = 2a + 2m + 2n + 2p + q > 2a + m + n = a + c.
So d + e > a + c.
So we have shown that a + c > a + b and a + c is smaller than the eight other possible sums.
Therefore, a + c is the second smallest sum. (It is also possible to use the above information to
show that c + e is the second largest sum.)