* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download ch10_shm_16slides
Jerk (physics) wikipedia , lookup
Old quantum theory wikipedia , lookup
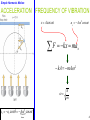
Classical mechanics wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Brownian motion wikipedia , lookup
Work (thermodynamics) wikipedia , lookup
Work (physics) wikipedia , lookup
Deformation (mechanics) wikipedia , lookup
Classical central-force problem wikipedia , lookup
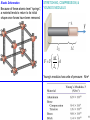
Centripetal force wikipedia , lookup
Equations of motion wikipedia , lookup
Seismometer wikipedia , lookup
Viscoelasticity wikipedia , lookup
Newton's laws of motion wikipedia , lookup
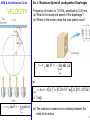
Ch 10. Harmonic Motion & Elasticity Example 1 A Tire Pressure Gauge Ideal Spring & Simple Harmonic Motion The spring constant is 320 N/m and the bar indicator extends 2.0 cm. What force does the air in the tire apply on the spring? HOOKE’S LAW: Fx k x The restoring force on an ideal spring k = spring constant Units: N/m FxApplied k x 320 N m 0.020 m 6.4 N 1 10.2 Simple Harmonic Motion and Reference Circle x A cos A cos t amplitude A: maximum displacement period T: time to complete one cycle frequency f: number of cycles per second (Hz) 1 f T 2 2 f T 2 SHM & the Reference Circle VELOCITY Ex. 3 Maximum Speed of Loudspeaker Diaphragm Frequency of motion is 1.0 KHz, amplitude is 0.20 mm. (a) What is the maximum speed of the diaphragm? (b) Where in the motion does this max speed occur? v x vT sin A sin t vmax (a) vmax A A2 f 0.20 103 m 2 1.0 103 Hz 1.3 m s v x vT sin A sin t vmax (b) The maximum speed occurs midway between the ends of its motion. 3 Simple Harmonic Motion ACCELERATION FREQUENCY OF VIBRATION x A cos t a x A 2 cos t F kx ma x kA mA 2 k m ax ac cos A 2 cos t amax 4 Simple Harmonic Motion Example 6 A Body Mass Measurement Device k mtotal The device below consists of a springmounted chair in which the astronaut sits. The spring has a spring constant of 606 N/m and the mass of the chair is 12.0 kg. The measured period is 2.41 s. Find the mass of the astronaut. mtotal k 2 2 2 f T mtotal k mchair mastro 2 2 T k mastro mchair 2 2 T 2 606 N m 2.41 s 12.0 kg 77.2 kg 4 2 5 10.3 Energy and Simple Harmonic Motion A compressed spring can do work. Welastic F cos s 12 kxo kxf cos 0 xo x f Welastic 12 kxo2 12 kx2f ELASTIC POTENTIAL ENERGY The elastic potential energy is the energy that a spring has by virtue of being stretched or compressed. For an ideal spring, the elastic potential energy is PEelastic 12 kx2 Units: joule (J) 6 Energy and Simple Harmonic Motion Example 8 Changing the Mass of a Simple Harmonic Oscilator A 0.20-kg ball is attached to a vertical spring. The spring constant is 28 N/m. When released from rest, how far does the ball fall before being brought to a momentary stop by the spring? E f Eo 1 2 1 2 mv2f 12 I 2f mghf 12 ky2f 12 mvo2 12 Io2 mgho 12 kyo2 kho2 mgho 2mg ho k 20.20 kg 9.8 m s 2 0.14 m 28 N m 7 10.4 The Pendulum A simple pendulum consists of a particle attached to a frictionless pivot by a cable of negligible mass. g L mgL I (small angles only) Example 10 Keeping Time Determine the length of a simple pendulum that will swing back and forth in simple harmonic motion with a period of 1.00 s. 2 2 f T g L T 2g L 4 2 (small angles only) T 2 g 1.00 s 9.80 m s 2 L 0.248 m 2 2 4 4 2 8 Damped Harmonic Motion In simple harmonic motion, an object oscillated with a constant amplitude. In reality, friction is always present and amplitude decreases with time. This is damped harmonic motion. 1) simple harmonic motion 2&3) underdamped 4) critically damped 5) overdamped 9 Driven Harmonic Motion & Resonance When a force is applied to an oscillating system at all times, the result is driven harmonic motion. Here, the driving force has the same frequency as the spring system and always points in the direction of the object’s velocity. RESONANCE Resonance is the condition in which a time-dependent force can transmit large amounts of energy to an oscillating object, leading to a large amplitude motion. Resonance occurs when the frequency of the force matches a natural frequency at which the object will oscillate. 10 Elastic Deformation Because of these atomic-level “springs”, a material tends to return to its initial shape once forces have been removed. STRETCHING, COMPRESSION, & YOUNG’S MODULUS L A F Y Lo Young’s modulus has units of pressure: N/m2 11 Elastic Deformation Example 12 Bone Compression In a circus act, a performer supports the combined weight (1080 N) of a number of colleagues. Each thighbone of this performer has a length of 0.55 m and an effective cross sectional area of 7.7×10-4 m2. Determine the amount that each thighbone compresses under the extra weight. L A F Y Lo FLo L YA 540 N 0.55 m 9.4 10 9 N m 2 7.7 10 4 m 2 4.1105 m 12 Elastic Deformation SHEAR DEFORMATION & SHEAR MODULUS x F S A Lo The shear modulus has the units of pressure: N/m2 13 Elastic Deformation Example 14 J-E-L-L-O You push tangentially across the top surface with a force of 0.45 N. The top surface moves a distance of 6.0 mm relative to the bottom surface. What is the shear modulus of Jell-O? x F S A Lo FLo S Ax 0.45 N 0.030 m S 460 N 2 3 0.070 m 6.0 10 m m2 14 Elastic Deformation VOLUME DEFORMATION & BULK MODULUS V P B Vo The Bulk modulus has the units of pressure: N/m2 15 10.8 Stress, Strain, and Hooke’s Law In general the quantity F/A is called the stress. The change in the quantity divided by that quantity is called the strain: V Vo L Lo x Lo HOOKE’S LAW FOR STRESS AND STRAIN Stress is directly proportional to strain. Strain is a unitless quantitiy. SI Unit of Stress: N/m2 16