Download Ch6Lecture2

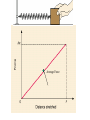
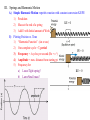
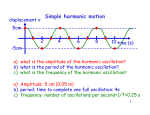
CH 6 Lecture 2 Conservation of Energy
I.
Elastic Potential Energy
A.
Pushing/Pulling on a spring
1) Stretching or compressing an object from a preferred state requires work
2) The force opposing is elastic if the object snaps back into shape
3) We give the object Elastic Potential Energy
B.
Springs
1) Spring constant = k
(Tells us how stiff the spring is)
2) Stiffer the spring, larger k
3) Force of spring is proportional to distance it is stretched/compressed
4) Hooke’s Law F = -kx (x = distance stretched or compressed)
a) -k means spring force is always opposing its motion
F  - kx  N  - km
b) Push on the spring, it pushes back
kgm
c) Pull on the spring, it pulls back
 2  km  - k  kg/s 2
s
C.
1 2
Elastic Potential Energy = kx
2
k = 2 kg/s, x = 5 m, F?, W?, PE?
W  PE  Fd  (kx) x  kx2
½ comes from avg force being half max. force
Average Force
II.
Conservation of Energy
A) Total Energy of a system remains the same unless it is acted on by an external
force
KE + PE = constant
B)
C)
Pendulum
1) Side1: KE = 0, Total E = PE
2) Bottom: PE = 0, KE = Total E
3) Side2: KE = 0, Total E = PE
F
4) Work to get this started, after that W = 0
a) Input E into the system
b) ET = KE + PE = constant
c) Sides: Initial Work gives us PE
d) Bottom: Gravity moves bob down (KE)
e) F = tension = centripetal force; perpendicular to motion, W = Fd = 0
f) Friction (air resistance) does small work, eventually stopping bob
g) In a vacuum, the pendulum would keep swinging forever
Could we describe the pendulum with Newton’s laws?
1) Velocity is continually changing
2) Calculations would be hard
D) Use Conservation of Energy to Solve hard Mechanics problems
1) Pendulum, m = 0.5 kg h = 12 cm v at bottom?
At top, ET = PE = mgh = (0.5kg)(9.8m/s)(0.12m) = 0.588 J
At bottom, ET = KE = ½ mv2 = (0.5)(0.5kg)v2 = 0.588 J
E)
Energy on a mountain
v2 = 2.35 m2/s2
v = 1.53 m/s
KE = ½ mv2
If KE decreases, v decreases
III. Springs and Harmonic Motion
A) Simple Harmonic Motion: repetitive motion with constant conversion KE/PE
1) Pendulum
KE = 0
2) Mass at the end of a spring
3) Add E with Initial amount of Work
B) Plotting Position vs. Time
1) “Harmonic Function” (sin or cos)
2) One complete cycle = T, period
PE = 0
-1
3) Frequency = # cycles per second (Hz = s )
4) Amplitude = max. distance from starting pt.
5) Frequency for
a) Loose/Tight spring?
KE = 0
b) Large/Small mass?
C) Restoring Forces lead to Harmonic Motion
1) Wants to bring mass back to starting position
2) If F is proportional to d, get harmonic motion (F = -kx)
3) What is restoring force for a simple pendulum?
D) Case of a vertical spring/mass system
1) Force of Gravity pulling down is constant
2) Restoring force pulling up varies
FT = FR + FG
3) Equilibrium point is lower than without gravity
4) Harmonic Motion just like horizontal setup
5) FT is still proportional to x
6) PE = gravity + elastic potential energy
Animations