Download Linear Regression

Linear Regression
Exploring relationships
between two metric variables
Correlation
• The correlation coefficient
measures the strength of a
relationship between two variables
• The relationship involves our ability
to estimate or predict a variable
based on knowledge of another
variable
Linear Regression
• The process of fitting a straight line to
a pair of variables.
• The equation is of the form: y = a + bx
• x is the independent or explanatory
variable
• y is the dependent or response
variable
Linear Coefficients
• Given x and y, linear regression
estimates values for a and b
• The coefficient a, the intercept,
gives the value of y when x=0
• The coefficient b, the slope, gives
the amount that y increases (or
decreases) for each increase in x
x=1:5
y <- 2.5*x + 1
plot(y~x, xlim=c(0, 5), ylim=c(0, 14),
yaxp=c(0, 14, 14), las=1, pch=16)
abline(lm(y~x))
points(0, 1, pch=8)
points(mean(x), mean(y), cex=3)
segments(c(1, 2), c(3.5, 3.5), c(2, 2), c(3.5, 6))
text(c(1.5, 2.25), c(3, 4.75), c("1", "2.5"))
text(mean(x), mean(y), "x = mean(x), y = mean(y)",
pos=4, offset=1)
text(0, 1, "y-intercept = 1", pos=4)
text(1.5, 5, "slope = 2.5/1 = 2.5", pos=2)
text(2, 12, "y = 1 + 2.5x", cex=1.5)
Least Squares
• Many lines could fit the data
depending on how we define the
“best fit”
• Least squares regression minimizes
the squared deviations between the
y-values and the line
lm()
• Function lm() performs least
squares linear regression in R
• Formula used to indicate
Dependent/Response from
Independent/Explanatory
• Tilde(~) separates them D~I or R~E
• Rcmdr Statistics | Fit model | Linear
regression
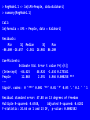
> RegModel.1 <- lm(LMS~People, data=Kalahari)
> summary(RegModel.1)
Call:
lm(formula = LMS ~ People, data = Kalahari)
Residuals:
Min
1Q
-86.400 -24.657
Median
-2.561
3Q
24.902
Max
86.100
Coefficients:
Estimate Std. Error t value
(Intercept) -64.425
44.924 -1.434
People
12.868
2.591
4.966
--Signif. codes: 0 '***' 0.001 '**' 0.01
Pr(>|t|)
0.175161
0.000258 ***
'*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 47.88 on 13 degrees of freedom
Multiple R-squared: 0.6548,
Adjusted R-squared: 0.6282
F-statistic: 24.66 on 1 and 13 DF, p-value: 0.0002582
plot(LMS~People, data=Kalahari, pch=16, las=1)
RegModel.1 <- lm(LMS~People, data=Kalahari)
abline(Line)
segments(Kalahari$People, Kalahari$LMS, Kalahari$People,
RegModel.1$fitted, lty=2)
text(12, 250, paste("y = ",
as.character(round(RegModel.1$coefficients[[1]], 2)),
" + ",
as.character(round(RegModel.1$coefficients[[2]], 2)),
"x", sep=""), cex=1.25, pos=4)
Errors
• Linear regression assumes all
errors are in the measurement of y
• There are also errors in the
estimation of a (intercept) and b
(slope)
• Significance for a and b is based on
the t distribution
Errors 2
• The errors in the intercept and slope
can be combined to develop a
confidence interval for the
regression line
• We can also compute a prediction
interval which is the confidence we
have in a single prediction
predict()
• predict() uses the results of a linear
regression to predict the values of
the dependent/response variable
• It can also produce confidence and
prediction intervals:
– predict(RegModel.1, data.frame(People
= c(10, 20, 30)), interval="prediction")
RegModel.1 <- lm(LMS~People, data=Kalahari)
plot(LMS~People, data=Kalahari, pch=16, las=1)
xp<-seq(10,25,.1)
yp<-predict(RegModel.1,data.frame(People=xp),int="c")
matlines(xp,yp, lty=c(1,2,2),col="black")
yp<-predict(RegModel.1,data.frame(People=xp),int="p")
matlines(xp,yp, lty=c(1,3,3),col="black")
legend("topleft", c("Confidence interval (95%)",
"Prediction interval (95%)"),
lty=c(2, 3))
Diagnostics
• Models | Graphs | Basic diagnostic
plots
– Look for trend in residuals
– Look for change in residual variance
– Look for deviation from normally
distributed residuals
– Look for influential data points
Diagnostics 2
• influence(RegModel.1) returns
–
–
–
–
Hat (leverage) coefficients
Coefficient changes (leave one out)
Sigma, residual changes (leave one out)
wt.res, weighted residuals
Other Approaches
• rlm() fits a robust line that is less
influenced by outliers
• sma() in package smatr fits
standardized major axis (aka
reduced major axis) regression and
major axis regression – used in
allometry