* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Linear Regression
Survey
Document related concepts
Transcript
Linear Regression
Exploring relationships
between two metric variables
Correlation
• The correlation coefficient
measures the strength of a
relationship between two variables
• The relationship involves our ability
to estimate or predict a variable
based on knowledge of another
variable
Linear Regression
• The process of fitting a straight line to
a pair of variables.
• The equation is of the form: y = a + bx
• x is the independent or explanatory
variable
• y is the dependent or response
variable
Linear Coefficients
• Given x and y, linear regression
estimates values for a and b
• The coefficient a, the intercept,
gives the value of y when x=0
• The coefficient b, the slope, gives
the amount that y increases (or
decreases) for each increase in x
x=1:5
y <- 2.5*x + 1
plot(y~x, xlim=c(0, 5), ylim=c(0, 14),
yaxp=c(0, 14, 14), las=1, pch=16)
abline(lm(y~x))
points(0, 1, pch=8)
points(mean(x), mean(y), cex=3)
segments(c(1, 2), c(3.5, 3.5), c(2, 2), c(3.5, 6))
text(c(1.5, 2.25), c(3, 4.75), c("1", "2.5"))
text(mean(x), mean(y), "x = mean(x), y = mean(y)",
pos=4, offset=1)
text(0, 1, "y-intercept = 1", pos=4)
text(1.5, 5, "slope = 2.5/1 = 2.5", pos=2)
text(2, 12, "y = 1 + 2.5x", cex=1.5)
Least Squares
• Many lines could fit the data
depending on how we define the
“best fit”
• Least squares regression minimizes
the squared deviations between the
y-values and the line
lm()
• Function lm() performs least
squares linear regression in R
• Formula used to indicate
Dependent/Response from
Independent/Explanatory
• Tilde(~) separates them D~I or R~E
• Rcmdr Statistics | Fit model | Linear
regression
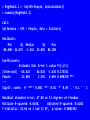
> RegModel.1 <- lm(LMS~People, data=Kalahari)
> summary(RegModel.1)
Call:
lm(formula = LMS ~ People, data = Kalahari)
Residuals:
Min
1Q
-86.400 -24.657
Median
-2.561
3Q
24.902
Max
86.100
Coefficients:
Estimate Std. Error t value
(Intercept) -64.425
44.924 -1.434
People
12.868
2.591
4.966
--Signif. codes: 0 '***' 0.001 '**' 0.01
Pr(>|t|)
0.175161
0.000258 ***
'*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 47.88 on 13 degrees of freedom
Multiple R-squared: 0.6548,
Adjusted R-squared: 0.6282
F-statistic: 24.66 on 1 and 13 DF, p-value: 0.0002582
plot(LMS~People, data=Kalahari, pch=16, las=1)
RegModel.1 <- lm(LMS~People, data=Kalahari)
abline(Line)
segments(Kalahari$People, Kalahari$LMS, Kalahari$People,
RegModel.1$fitted, lty=2)
text(12, 250, paste("y = ",
as.character(round(RegModel.1$coefficients[[1]], 2)),
" + ",
as.character(round(RegModel.1$coefficients[[2]], 2)),
"x", sep=""), cex=1.25, pos=4)
Errors
• Linear regression assumes all
errors are in the measurement of y
• There are also errors in the
estimation of a (intercept) and b
(slope)
• Significance for a and b is based on
the t distribution
Errors 2
• The errors in the intercept and slope
can be combined to develop a
confidence interval for the
regression line
• We can also compute a prediction
interval which is the confidence we
have in a single prediction
predict()
• predict() uses the results of a linear
regression to predict the values of
the dependent/response variable
• It can also produce confidence and
prediction intervals:
– predict(RegModel.1, data.frame(People
= c(10, 20, 30)), interval="prediction")
RegModel.1 <- lm(LMS~People, data=Kalahari)
plot(LMS~People, data=Kalahari, pch=16, las=1)
xp<-seq(10,25,.1)
yp<-predict(RegModel.1,data.frame(People=xp),int="c")
matlines(xp,yp, lty=c(1,2,2),col="black")
yp<-predict(RegModel.1,data.frame(People=xp),int="p")
matlines(xp,yp, lty=c(1,3,3),col="black")
legend("topleft", c("Confidence interval (95%)",
"Prediction interval (95%)"),
lty=c(2, 3))
Diagnostics
• Models | Graphs | Basic diagnostic
plots
– Look for trend in residuals
– Look for change in residual variance
– Look for deviation from normally
distributed residuals
– Look for influential data points
Diagnostics 2
• influence(RegModel.1) returns
–
–
–
–
Hat (leverage) coefficients
Coefficient changes (leave one out)
Sigma, residual changes (leave one out)
wt.res, weighted residuals
Other Approaches
• rlm() fits a robust line that is less
influenced by outliers
• sma() in package smatr fits
standardized major axis (aka
reduced major axis) regression and
major axis regression – used in
allometry