Download 6.S092: Visual Recognition through Machine Learning Competition

6.S093 Visual Recognition through
Machine Learning Competition
Joseph Lim and Aditya Khosla
Acknowledgment: Many slides from David Sontag and Machine Learning Group of UT Austin
Image by
kirkh.deviantart.com
What is Machine Learning???
What is Machine Learning???
According to the Wikipedia,
Machine learning concerns the construction and study of systems that
can learn from data.
What is ML?
• Classification
– From data to discrete classes
What is ML?
• Classification
– From data to discrete classes
• Regression
– From data to a continuous value
What is ML?
• Classification
– From data to discrete classes
• Regression
– From data to a continuous value
• Ranking
– Comparing items
What is ML?
• Classification
– From data to discrete classes
• Regression
– From data to a continuous value
• Ranking
– Comparing items
• Clustering
– Discovering structure in data
What is ML?
• Classification
– From data to discrete classes
• Regression
– From data to a continuous value
• Ranking
– Comparing items
• Clustering
– Discovering structure in data
• Others
Classification:
data to discrete classes
• Spam filtering
Spam
Regular
Urgent
Classification:
data to discrete classes
• Object classification
Fries
Hamburger
None
Regression: data to a value
• Stock market
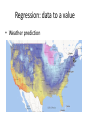
Regression: data to a value
• Weather prediction
Clustering: Discovering structure
Set of Images
Clustering
Clustering
• Unsupervised learning
• Requires data, but NO LABELS
• Detect patterns
– Group emails or search results
– Regions of images
• Useful when don’t know what you’re looking
for
Clustering
• Basic idea: group together similar instances
• Example: 2D point patterns
Clustering
• Basic idea: group together similar instances
• Example: 2D point patterns
Clustering
• Basic idea: group together similar instances
• Example: 2D point patterns
Clustering
• Basic idea: group together similar instances
• Example: 2D point patterns
• What could “similar” mean?
– One option: small Euclidean distance
– Clustering is crucially dependent on the measure
of similarity (or distance) between “points”
K-Means
• An iterative clustering
algorithm
– Initialize: Pick K random
points as cluster centers
– Alternate:
• Assign data points to
closest cluster center
• Change the cluster center
to the average of its
assigned points
– Stop when no points’
assignments change
Animation is from Andrey A. Shabalin’s website
K-Means
• An iterative clustering algorithm
– Initialize: Pick K random points as cluster centers
– Alternate:
• Assign data points to closest cluster center
• Change the cluster center to the average of its assigned
points
– Stop when no points’ assignments change
Properties of K-means algorithm
• Guaranteed to converge in a finite number of
iterations
• Running time per iteration:
– Assign data points to closest cluster center
O(KN)
– Change the cluster center to the average of its
assigned points
O(N)
Example: K-Means for Segmentation
K=2
Original
Goal of Segmentation
is to partition an image
into regions each of
which has reasonably
homogenous visual
appearance.
Example: K-Means for Segmentation
K=2
K=3
K=10
Original
Pitfalls of K-Means
• K-means algorithm is heuristic
– Requires initial means
– It does matter what you pick!
• K-means can get stuck
K=1 should be better
K=2 should be better
Classification
Typical Recognition System
+1 bus
features
x
classify
-1 not bus
F(x)
• Extract features from an image
• A classifier will make a decision based on
extracted features
y
Typical Recognition System
+1 bus
features
x
classify
-1 not bus
F(x)
• Extract features from an image
• A classifier will make a decision based on
extracted features
y
Classification
• Supervised learning
• Requires data, AND LABELS
• Useful when you know what you’re looking for
Linear classifier
• Which of these linear separators is optimal?
Maximum Margin Classification
• Maximizing the margin is good according to intuition and PAC
theory.
• Implies that only support vectors matter; other training
examples are ignorable.
Classification Margin
wT xi  b
r
w
• Distance from example xi to the separator is
• Examples closest to the hyperplane are support vectors.
• Margin ρ of the separator is the distance between support
vectors.
ρ
r
Linear SVM Mathematically
• Let training set {(xi, yi)}i=1..n, xi  Rd, yi  {-1, 1} be separated by a
hyperplane with margin ρ. Then for each training example (xi, yi):
wTxi + b ≤ - ρ/2
wTxi + b ≥ ρ/2
if yi = -1
yi(wTxi + b) ≥ ρ/2

if yi = 1
• For every support vector xs the above inequality is an equality.
After rescaling w and b by ρ/2 in the equality, we obtain that
distance between each xs and the hyperplane is
y s (wT x s + b)
r=
w
=
1
w
• Then the margin can be expressed through (rescaled) w and b as:
  2r 
2
w
Linear SVMs Mathematically (cont.)
• Then we can formulate the quadratic
optimization problem:
Find w and b such that
r=
2
is maximized
w
and for all (xi, yi), i=1..n : yi(wTxi + b) ≥ 1
Find w and b such that
Φ(w) = ||w||2=wTw is minimized
and for all (xi, yi), i=1..n : yi (wTxi + b) ≥ 1
Is this perfect?
Is this perfect?
Soft Margin Classification
• What if the training set is not linearly separable?
• Slack variables ξi can be added to allow
misclassification of difficult or noisy examples,
resulting margin called soft.
ξi
ξi
Soft Margin Classification
Mathematically
• The old formulation:
Find w and b such that
Φ(w) =wTw is minimized
and for all (xi ,yi), i=1..n :
yi (wTxi + b) ≥ 1
• Modified formulation incorporates slack variables:
Find w and b such that
Φ(w) =wTw + CΣξi is minimized
and for all (xi ,yi), i=1..n :
yi (wTxi + b) ≥ 1 – ξi, ,
ξi ≥ 0
• Parameter C can be viewed as a way to control
overfitting: it “trades off” the relative importance
of maximizing the margin and fitting the training
data.
Exercise
• Exercise 1. Implement K-means
• Exercise 2. Play with SVM’s C-parameter