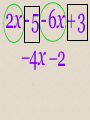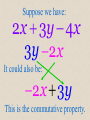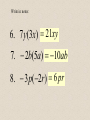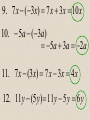Download 2.3 combining like terms powerpoint

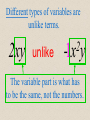
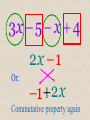
Combining Like
Terms
in
Algebra County
2x - 5- 6x  3
4x 2
Different types of variables are
unlike terms.
4x
2
unlike 8x
To be like terms, the variable part
is what has to be the same,
not the numbers.
Different types of variables are
unlike terms.
2xy
unlike
2
-1x y
The variable part is what has
to be the same, not the numbers.
These are like terms even though
they contain both an x and a y.
3xy
LIKE
-9xy
These are also like terms.
1xy
LIKE
1yx
We write variables in
alphabetical order.
Even if we put numbers in front
(coefficients) of each variable,
they are still like terms.
5 xy LIKE -3 yx
Suppose we have:
2 x  3y  4 x
3y 2x
It could also be:
2x  3y
This is the commutative property.
3x  5  x  4
2x  1
Or:
1  2x
Commutative property again
The Adding Song
Sung in
Algebra County
to the tune of
“Hark! The Herald Angels Sing”
When in math we do addition
We must always add like things.
To add decimals, we must line up
Corresponding place values.
To add fractions, we’re in need of
Like denomina-ators,
In Algebra, we need like terms;
They stay the same after we add,
In Algebra, we need like terms;
They stay the same after we add.
The Multiplying
Song
Sung in
Algebra County
to the tune of
“Hark! The Herald Angels Sing”
When we multiply two terms
They don’t have to be alike.
First we multiply the numbers,
Next, of course, the variables.
When we write the final product
Here’s the order of the factors:
Number first, the letters next,
Recorded alphabetically,
Number first, the letters next,
Recorded alphabetically.
Write in notes:
1. 7(3x)  21x
2.  2(5a)  10a
3.  3(10 x)  30x
4. 4(4 y)  16 y
5.  (7 y)  7 y
Write in notes:
6. 7 y(3x)  21xy
7.  2b(5a)  10ab
8.  3 p(2r )  6 pr
9. 7 x  (3x)  7 x  3x  10 x
10.  5a  (3a)
 5a  3a  2a
11. 7 x  (3x)  7 x  3 x  4 x
12. 11y  (5 y)  11y  5 y  6 y
13. 7 x  8 y  9 y  2 x  9x  y
14. 3x  4 x  x  2 x  4 x
2
2
2
15. 2 x  5  8 x  3  10 x  8
16.  3  4 y  3x  same
to Algebra County