Download Mass-spring system Simple Model Application of the momentum

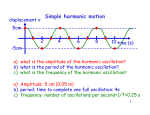
Harmonic Oscillator
Objective: Describe the position as a function of time of a harmonic oscillator. Apply the momentum
principle to a harmonic oscillator. Sketch (and interpret) a graph of position as a function of time for a
harmonic oscillator.
Mass-spring system
We are modeling a solid as a bunch of balls (atoms) connected by springs (interatomic bonds). We’ve studied
the stiffness of a spring, and we understand that the force required to stretch an ideal spring a distance s
from its unstretched position is
F = ks s
(1)
where ks is the stiffness of the spring. Now, we will apply this equation to a mass attached to an ideal spring
that is initially stretched when we let it go. What will be the resulting motion of the spring?
Answering this question is important because it improves our model of a solid. The atoms in a solid are
moving (i.e. vibrating), sometimes more vigorously than at other times, depending on its temperature. In
order to understand the motion of the atoms and to relate their motion to properties like temperature, we
need to understand the behavior of mass oscillating on a spring.
Simple Model
Let;s begin with a simplified system. Suppose we have an object (i.e. particle) of mass m attached to spring.
It is in space, far from any gravitational or electromagnetic interactions. Thus, the only thing interacting
with the mass is a spring (the other end of the spring is attached to a rigid wall of some kind, but we assume
this does not interact with our mass).
The spring is initially unstretched. Then, we pull the object back from this position and release it from
rest.
Application of the momentum principle
According to the momentum principle,
∆~
p = F~net ∆t
(2)
But, what is the net force acting on the object? Here’s a little help in identifying the net force on an
object:
1. Identify the object in question.
2. Identify what other objects interact with it. An interaction can be a long-range interaction such as
gravitation or electromagnetic interactions, or it can be due to contact (this is fundamentally electromagnetic in nature, but more easily identified as due to contact).
3. Determine the nature of any of these interactions, writing each known force as an equation or as a
measured value. Write known forces as vectors!
4. Write the net force as a sum of all the forces on the object.
Once you do that, you are able to apply the momentum principle. In this case, the net force acting on the
object is only the force of the spring on the object. That’s because the spring is the only thing interacting
with the object. A picture of the situation is shown below:
The force of the spring on the object is
F = −ks x
(3)
That is because when x is positive, this spring is stretched and therefore pulls to the left. If x is negative,
the spring is compressed and pushes to the right. The spring only exerts a force along the x-axis; therefore,
the net force on the object is
F~net =< −ks x, 0, 0 >
(4)
Applying the momentum principle gives
∆~
p =< −ks x, 0, 0 > ∆t
(5)
Now we can apply our technique of numerical integration to understand what the x-position of the object as
a function of time will be. We follow the same procedure as before to write our program. Here’s the general
procedure:
1. Calculate the net force on the object when it’s at position x.
2. Calculate the new momentum of the object after time interval dt.
3. Calculate the new position of the object after time interval dt.
4. Repeat over and over.
You will write this simulation during lab this week. An example of the resulting graph of position as a
function of time looks like one shown in Figure 1.
Figure 1: x vs. t for mass-spring system
Note that the position as a function of time is periodic. If you do a curve fit to this particular graph,
you will find that the position is given by
x = Acos(ωt)
(6)
where A is the amplitude of the oscillation and ω is the angular frequency in rad/s. The amplitude is the
maximum displacement (+ or –) of the object from its equilibrium position. The angular frequency, ω, tells
you how many oscillations occur in a given time interval, but it is in units of radians where 2π radians is
one oscillation (or one cycle). It’s related to the frequency, f , which is the number of oscillations, or cycles,
per second. Therefore,
ω = 2πf
(7)
Since the frequency (the number of cycles per second) is the inverse of the period (the time interval in
one cycle), then
2π
T
What is the amplitude and angular frequency of the graph shown in Figure 1?
ω=
(8)
Analytic Solution
Sometimes the momentum principle can be solved analytically–it can be solved without using numerical
integration. First, let’s write the momentum principle in differential form.
d~
p
F~net =
dt
If the mass of the object remains constant, then
(9)
d~v
F~net = m
(10)
dt
In this case, we only have an x-component of the net force. Substituting the net force and evaluating
only the x-component gives
−ks x = m
d2 x
dvx
=m 2
dt
dt
(11)
This is often written as
d2 x ks
+ x=0
(12)
dt
m
This is called a differential equation, and you will learn how to solve these equations in a Differential
Equations class. However, for right now, we will just right down the general solution.
r
ks
x = Acos(
t + φ)
(13)
m
where A is the amplitude and φ is the phase. By comparing this to our simulation, we can see that the
angular frequency is related to the spring constant and mass of the system.
r
ks
ω=
(14)
m
which means that we can write the period of oscillation as
r
m
T = 2π
(15)
k
The phase, φ, is related to the initial conditions, x0 and vx0 , of the oscillator. Think of the phase in this
way–depending on when you start the clock (t=0), the phase tells you where the function starts. If φ = 0,
then the function is at its peak (x = xm ) at t=0. If the phase is π/2, then the function is at x = 0 at t=0,
but with a negative slope. If φ = π, then the function is at its minimum (x = −xm ) at t=0. If the phase is
3π/2, then the function is at x = 0 at t=0, but with a positive slope.
Graphs of x as a function of time in Figures 2–4 demonstrate harmonic motion with a period of 4 seconds
but with different phases.
Application
1. A very light spring is attached between the end of a cart track and a 1.5 kg cart. The spring is
compressed 0.5 m from its equilibrium position and released. As a result, the cart oscillates in simple
harmonic motion. Position and time data as the cart travels from one turning point to the other are
shown below.
(a) What is the amplitude of the oscillation?
(b) What is the period of the oscillation?
(c) What is the spring constant of the spring?
(d) For 0 < t < 0.30 s, does the cart speed increase, decrease, or remain constant?
(e) For 0 < t < 0.30 s, is the cart velocity positive, negative, or zero?
(f) For 0 < t < 0.30 s, does the magnitude of the carts acceleration increase, decrease, or remain
constant?
(g) For 0 < t < 0.30 s, is the carts acceleration positive, negative, or zero?
(h) At what position(s) is v=0?
(i) At what position(s) is a=0?
(j) What is the maximum speed of the cart?
(k) What is the potential energy at t=0.15 s?
(l) What is the kinetic energy at t=0.15 s?
(m) Sketch graphs of x, vx , and ax as a function of time.
2. An object of mass 0.050 kg oscillates in simple harmonic motion with a period of 0.20 s and an
amplitude of 5.0 mm. At t=0, the object is at x=0 and is moving in the –x direction.
(a) Write the equation of motion for the object (with position in meters).
(b) What is the equation for the objects velocity as a function of time?
(c) What is the equation for the objects acceleration as a function of time?
3. You do an experiment with a cart on a track attached to a compressible spring. Each time you repeat
the experiment, you pull the cart back and release it from rest.
(a) If you double the mass of the cart, what happens to the period?
(b) If you double the spring constant of the spring, what happens to the period?
(c) If you double the amplitude, what happens to the period?
(d) Suppose the period of oscillation was 0.5 seconds and you want to make the period of oscillation
1.0 s. What would you do?
Figure 2: T = 4 s, φ = 0
Figure 3: T = 4 s, φ = π/2
Figure 4: T = 4 s, φ = π