Download Definition - WordPress.com

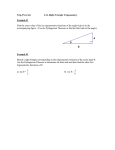
Handout 2 MAT199
July – Nov. 2010
________________________________________________________________
Adapted from Howard Anton, Calculus 8th edition
_______________________________________________________________________
rajasulaiman.wordpress.com
20
Handout 2 MAT199
July – Nov. 2010
________________________________________________________________
2.1 Derivatives and Integrals involving Inverse Trigonometric Functions
Inverse Trigonometric Functions
The six basic trigonometric functions do not have inverse because their graphs
repeat periodically and hence do not satisfy the horizontal line test.
Can we still find the inverses?
Definition
The inverse sine function, denoted by sin1 , is defined to be the inverse of the


restricted sine function sin x ,   x 
2
2
Definition
The inverse cosine function, denoted by cos 1 , is defined to be the inverse of
the restricted cosine function cos x , 0  x  
Definition
The inverse tangent function, denoted by tan 1 , is defined to be the inverse of


the restricted tangent function tan x ,  x 
2
2
Definition
The inverse secant function, denoted by sec 1 , is defined to be the inverse of

the restricted secant function ,0  x  , x 
2
_______________________________________________________________________
rajasulaiman.wordpress.com
21
Handout 2 MAT199
July – Nov. 2010
________________________________________________________________
Identities for Inverse Trigonometric functions
If we interpret sin1 x as an angle in radian measure whose sine is x, and if
that angle is nonnegative, then we can represent sin1 x geometrically as an
angle in a right triangle in which the hypotenuse has length 1 and the side
opposite to the angle sin1 x has length x.
Listed below are some useful identities involving inverse Trigonometric functions
which are valid for  1  x  1
sin1 x  cos1 x 







2
cos sin1 x  1  x2
sin cos1 x  1  x2
tan sin1 x 
x
1 x2
Simplifying Expression involving Inverse Trigonometric Functions
Triangle Method
In order to evaluate expression involving inverse trigonometric function, we can
represent the inverse trigonometric function as an angle in a right triangle.
_______________________________________________________________________
rajasulaiman.wordpress.com
22
Handout 2 MAT199
July – Nov. 2010
________________________________________________________________
Example 1
Determine the exact value without using a calculator:
sin1 1
Example 2
Determine the exact value without using a calculator:
 1 
sin1  
 2
Example 3
Determine the exact value without using a calculator:
 1
cos1  
2
Example 4

Without using the calculator, find the value of cos tan 1 3

Example 5


Use the triangle method to simplify tan cos ec 12y 
_______________________________________________________________________
rajasulaiman.wordpress.com
23
Handout 2 MAT199
July – Nov. 2010
________________________________________________________________
Example 6

Use the triangle method to evaluate sin tan 1 3  cos1(

1 
)  .
2 
Apr 2009
Derivative of inverse Trigonometric Functions
Motivation
Example 7
Find the derivative of y  sin1 x
_______________________________________________________________________
rajasulaiman.wordpress.com
24
Handout 2 MAT199
July – Nov. 2010
________________________________________________________________
Generalized Derivative Formula for Inverse Trigonometric Functions
If u is a differentiable function of x, the chain rule produces the following
generalized derivative formula:












1
d
1 du
sin u 
dx
1  u2 dx
1
d
1 du
cos u  
dx
1  u2 dx
1
d
1 du
tan u 
dx
1  u2 dx
1
d
1 du
cot u  
dx
1  u2 dx
1
d
1
du
sec u 
2
dx
u u  1 dx
1
d
1
du
csc u  
2
dx
u u  1 dx
_______________________________________________________________________
rajasulaiman.wordpress.com
25
Handout 2 MAT199
July – Nov. 2010
________________________________________________________________
Example 8
Find
 
dy
if y  sin1 x 4
dx
Example 9
Find
dy
if y  cos14x 
dx
Example 10
Find
 
dy
if y  tan1 x2
dx
Example 11
Find
dy
if y  e2 x sin13x 
dx
_______________________________________________________________________
rajasulaiman.wordpress.com
26
Handout 2 MAT199
July – Nov. 2010
________________________________________________________________
Integrals involving Inverse Trigonometric Functions

du
1 u
 1 u
du
u
2
2
 sin1 u  c
(1)
 tan 1 u  c
du
u 1
2
(2)
 sec 1 u  c
(3)
Example 12
Evaluate
 1  3x
dx
2
Hint: let u = _________
Example 13
Evaluate

ex
1  e 2x
dx
Hint: let u = _________
_______________________________________________________________________
rajasulaiman.wordpress.com
27
Handout 2 MAT199
July – Nov. 2010
________________________________________________________________
Example 14
Evaluate
a
2
dx
where a  0 is a constant.
 x2
Hint: let u = _________
Generalization Formula for (1), (2) and (3)

du
1
u
 tan 1  c
2
a
a
a u

u
2
du
a 2  u2
du
u2  a 2
 sin1

u
c
a
1
u
sec 1  c
a
a
_______________________________________________________________________
rajasulaiman.wordpress.com
28
Handout 2 MAT199
July – Nov. 2010
________________________________________________________________
Example 15
Evaluate

dx
2  x2
.
Let us try another example.
Example 16
Evaluate

x dx
9  x4
.
APR 2008
_______________________________________________________________________
rajasulaiman.wordpress.com
29