* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Activity 4.2.1 Similarity Transformations
Introduction to gauge theory wikipedia , lookup
Pythagorean theorem wikipedia , lookup
History of geometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euler angles wikipedia , lookup
Möbius transformation wikipedia , lookup
Perceived visual angle wikipedia , lookup
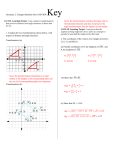
Name: Date: Page 1 of 2 Activity 4.2.1 Similarity Transformations In this lesson you will explore properties of similar polygons and which transformations produce similar figures. Open the file ctcoregeomACT421.ggb. Task 1: In quadrant 1 there is a dilation of preimage 𝐴𝐵𝐶𝐷 to image 𝐴′𝐵′𝐶′𝐷′. Use your selection tool to move each angle to coincide with its corresponding image. You can do this by selecting the center of dilation (E) and moving it until an angle and its image are on top of each other.. 1. What do you notice about the corresponding angles? 2. Now move E so that it is close to its original position as shown above. Record all sides and angle measures in this table: Angle Measures Polygon Side Lengths 𝑚∠𝐴 = 𝐴𝐵 = Distnaces from Center of Dilation to Vertices 𝐸𝐵 = 𝑚∠𝐴′ = 𝐴′ 𝐵 ′ = 𝐸𝐵 ′ = 𝑚∠𝐵 = 𝐵𝐶 = 𝐸𝐶 = 𝑚∠𝐵′ = 𝐵′𝐶′ = 𝐸𝐶 ′ = 𝑚∠𝐶 = 𝐶𝐷 = 𝐸𝐷 = 𝑚∠𝐶′ = 𝐶′𝐷′ = 𝐸𝐷′ = 𝑚∠𝐷 = 𝐴𝐷 = 𝐸𝐴 = 𝑚∠𝐷′ = 𝐴′ 𝐷′ = 𝐸𝐴′ = 3. What is the scale factor for this dilation? 4. Show that the ratios of the lengths of the sides of the image to the pre-image (A’B’/AB, etc.) are the same. Activity 4.2.1 Connecticut Core Geometry Curriculum Version 3.0 Name: Date: Page 2 of 2 Task 2: These three polygons are located in Quadrant II and III of the same Geogebra file as the previous task. Record all the angle measures and side lengths of the polygons in the table. Angles mF= Side Lengths FG= 5. Move point K. What do you observe? 6. What type of transformation maps Pentagon FGHIJ onto Pentagon QRSTU? Explain. 7. What type of transformation maps Pentagon FGHIJ onto Pentagon LMNOP? Explain. 8. What transformations would you use to map Pentagon LMNOP onto Pentagon QRSTU? Explain. 9. Which pair of pentagons, if any, are congruent? Explain. 10. Which pairs of pentagons have corresponding angles congruent and corresponding sides in proportion? 11. A similarity transformation is defined as a translation, rotation, reflection, or dilation or the composition of two or more of these transformations. Is the transformation that maps Pentagon LMNOP onto Pentagon QRSTU a similarity transformation? Explain. 12. Similar figures are defined as figures where one is the image of the other under a similarity transformation. Are all these polygons similar to one another? Explain. Activity 4.2.1 Connecticut Core Geometry Curriculum Version 3.0