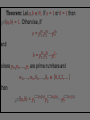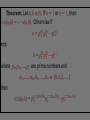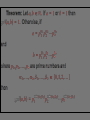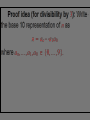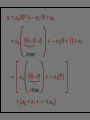* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Theory Associated With Natural Numbers
Survey
Document related concepts
Transcript
Part II – Theory and Computations Major Ideas.... Fundamental Theorem of Arithmetic (Prime Factorization Theorem) Each natural number n can be written as a product of prime numbers in one and only one way (except for the order of the factors). THEOREM: If n > 2 is a composite number, then n has a prime divisor p such that p n . CORLLARY: If n > 2 has no prime divisors p such that p n , then n is a prime number. APPLICATION: To test whether a number n is a prime you only have to check whether n is divisible by the primes p n . The numbers 2, 3, 5 and 7 determine primes < 100 5 The numbers 2, 3, 5 and 7 determine primes < 100 5 The primes above determine all primes < 10,000 Counting Factors... How can we count the factors of a number? For example: How many factors does 180 have? Counting Factors... Let n with n 2. If p1 , p2 ,..., pk are distinct prime numbers and 1 ,..., k 1, 2,... so that 1 n p1 k pk , then there are 1 1 k 1 factors of n. Proofs.... (The ones that can be explained to interested students.) Infinitely many primes, determining whether a number is prime, and divisibility by 3. Another Look... (with a possibility for generalization) Can you see what is happening in the following slide? In particular, what are the blue numbers? The blue numbers are the remainders from dividing 1, 10, 100, 1000, 10000, etc. by 3 Can you see what is happening in the following slide? In particular, what are the blue numbers? Notice the repetition!! The blue numbers are the remainders from dividing 1, 10, 100, 1000, 10000, etc. by 7 Can you state a give a conjecture concerning divisibility by 7? 1, 3, 2, 6, 4, 5, 1, 3, 2, 6, 4, 5, . . . Can you find the pattern for divisibility by 11? Can you find the pattern for divisibility by 11? Answer: 1,10,1,10,1,10,... Computations... Most calculators and computers use the Euclidean algorithm. TI-83 Programs... iPart, gcd and lcm – TI-83 commands PCHECK – (program) determines whether a number is prime. PFACT – (program) gives the prime factorization of a number.