Download Lecture 24

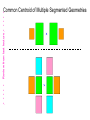
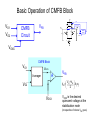
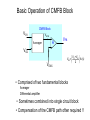
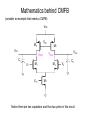
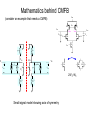
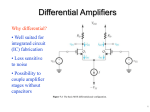
EE 435
Lecture 24
Common-Mode Feedback
Review from last lecture .• • • • •
.• • • • •
Offset Voltage
VOS
Can be modeled as a dc voltage source in series with the input
Random Offset Voltages
Review from last lecture .• • • • •
Correspondingly:
.• • • • •
 2VOS

 1
 1
1
1  
2
2
2


A n 
A  p  A COX 

 
2
2

Wp L p
 A VTOn  p L n
 Wn L n Wp L p  
VEBn Wn L n
2


 2

A VTOp 
2
4 
 1
 1
 Wn L n  n Wn L p
1 
1  
2
2

 Aw 

  2A L 


2
2 
2
2  

W
L
W
L
L
W
L
W
 n n
 n n
p p
p
p 


 

VDD
which again simplifies to
VX
 A2

μp Ln
2
2
VTO
n
σV  2 
+
A VTO p 
2
OS
Wn L n μ n Wn L p



M3
M4
VOUT
V1
M2
M1
VS
Note these offset voltage expressions are identical!
IT
V2
.• • • • •
Review from last lecture .• • • • •
Random Offset Voltages
VCC
VX
VX
Q3
V1
VCC
Q3
Q4
Q2
Q1
V2
V1
VE
Q4
Q2
Q1
VE
IT
(a)
It can be shown that
V2
OS
 A2
A 2Jp 

2Vt2  Jn +
 AEn AEp 


where very approximately
A Jn = A Jp = 0.1μ
IT
(b)
V2
Review from last lecture .• • • • •
Random Offset Voltages
Typical offset voltages:
MOS - 5mV to 50MV
BJT - 0.5mV to 5mV
These can be scaled with extreme device dimensions
.• • • • •
Often more practical to include offset-compensation circuitry
Review from last lecture .• • • • •
.• • • • •
Common Centroid Layouts
Define p to be a process parameter that varies with lateral position
throughout the region defined by the channel of the transistor.
Almost Theorem:
If p(x,y) varies linearly throughout a two-dimensional region, then
1
pEQ   px, y dxdy
AA
Parameters such at VT, µ and COX vary throughout a two-dimensional region
If a parameter varies linearly throughout a two-dimensional region, it is said
to have a linear gradient.
Review from last lecture .• • • • •
.• • • • •
Common Centroid Layouts
Almost Theorem:
If p(x,y) varies linearly throughout a two-dimensional region, then
pEQ=p(x0.y0) where x0,y0 is the geometric centroid to the region.
Parameters such at VT, µ and COX vary throughout a two-dimensional region
If a parameter varies linearly throughout a two-dimensional region, it is said
to have a linear gradient.
Many parameters have a dominantly linear gradient over rather small regions
Review from last lecture .• • • • •
.• • • • •
(x0,y0)
(x0,y0) is geometric centroid
pEQ
1
  px, y dxdy
AA
If ρ(x,y) varies linearly in any direction, then the theorem states
1
pEQ   p  x,y  dxdy  p  x0 ,y0 
AA
Review from last lecture .• • • • •
.• • • • •
Common Centroid Layouts
A layout of two devices is termed a common-centroid layout if both devices
have the same geometric centroid
Almost Theorem:
If p(x,y) varies linearly throughout a two-dimensional region, then if two
have the same centroid, the parameters are matched !
Note: This is true independent of the magnitude and direction of the gradient!
.• • • • •
Review from last lecture .• • • • •
Common Centroid of Multiple Segmented Geometries
Review from last lecture .• • • • •
.• • • • •
Common Centroid Layout Surrounded by
Dummy Devices
Common-Mode Feedback
VDD
M3
M4
VOXX
VOUT
VOUT
VIN
M1
M2
VIN
CL
CL
VB2
M9
Needs CMFB
Repeatedly throughout the course, we have added a footnote on fullydifferential circuits that a common-mode feedback circuit (CMFB) is
needed
The CMFB circuit is needed to establish or stabilize the operating point or
operating points of the op amp
Common-Mode Feedback
VDD
VDD
M3
VFB
M4
VB1
VOUT
VOUT
VIN
M1
M2
VIN
M3
M4
VOUT
VOUT
CL
CL
VIN
VB2
M1
M2
CMFB
Circuit
VIN
CL
CL
M9
VOXX
VB2
M9
On the reference op amp, the CMFB signal can be applied to either the pchannel biasing transistors or to the tail current transistor
It is usually applied only to a small portion of the biasing transistors though
often depicted as shown
There is often considerable effort devoted to the design of the CMFB though
little details are provided in most books and the basic concepts of the CMFB
are seldom rigorously developed and often misunderstood
Common-Mode Feedback
Partitioning biasing transistors for VFB insertion
(Nominal device matching assumed, all L’s equal)
VDD
VDD
VFB
M3
VOUT
VIN
M1
VB1
CL
VFB insertion
M9
VDD
M4
VB1
M3A M3B
M4B M4A
VFB
VDD
VFB
CMFB
Circuit
VIN
VOXX
Ideal (Desired) biasing
M3
M2
CL
VB2
M3
M4
VOUT
M4
Partitioned VFB insertion
W3A +W3B =W3
W3B <<W3A
VB1
Basic Operation of CMFB Block
VDD
VFB
VO1
VO2
CMFB
Circuit
VFB
M3
M4
VOUT
VOUT
VIN
M1
M2
CMFB
Circuit
VIN
CL
CL
VOXX
VB2
M9
VOXX
CMFB Block
VO1
VAVG
Averager
A
VFB
 V +V 
VFB =  01 02  A  s 
2 

VO2
VOXX
VOXX is the desired
quiescent voltage at the
stabilization node
(irrespective of where VFB goes)
Basic Operation of CMFB Block
CMFB Block
VO1
VAVG
Averager
A
VFB
VO2
VOXX
 V +V 
VFB =  01 02  A  s 
2 

• Comprised of two fundamental blocks
Averager
Differential amplifier
• Sometimes combined into single circuit block
• Compensation of the CMFB path often required !!
Mathematics behind CMFB
(consider an example that needs a CMFB)
VDD
VB1
M5
VO1
M4
VO2
VOXX
VOXX
C1
V1
M1
VYY
M2
V2
C2
M3
Notice there are two capacitors and thus two poles in this circuit
Mathematics behind CMFB
VDD
(consider an example that needs a CMFB)
VB1
M5
VO1
M4
VO2
VOXX
VOXX
C1
V1
M1
VYY
g05
VO2
M3
V2
gm2VGS2
gm1VGS1
VGS1
V2
g04
VO1
V1
M2
g01
g02
C1
C2
M’3
M3
VGS2
2W’3=W3
g03/2
g03/2
Small-signal model showing axis of symmetry
M’3
C2
Mathematics behind CMFB
(consider an example that needs a CMFB)
g05
g04
VO1
V1
VO2
V2
gm2VGS2
gm1VGS1
VGS1
g05
g01
g02
C1
g03/2
C2
g03/2
VOD
Vd
2
gm1VGS1
g01
VGS1
C
Small-signal difference-mode half circuit
VOD  sC+g01+g05  +gm1
gm1
2
A DIFF =
sC+g01+g05
-
pDIFF = -
g01+g05
C
Vd
0
2
Note there is a single-pole in this circuit
What happened to the other pole?
VGS2
Mathematics behind CMFB
(consider an example that needs a CMFB)
g05
g05
g04
VO1
V1
VO2
V2
gm2VGS2
gm1VGS1
VGS1
g01
g02
C1
C2
VGS2
VOC
VCOM
g03/2
g03/2
gm1VGS1
g01
VGS1
C
VS
g03/2
Standard small-signal common-mode half circuit
VOC  sC+g01+g05  +gm1  VCOM -VS   0
Note there is a single-pole in this circuit
VS  g01+g03 /2 -gm1  VCOM -VS   VOCg01
A COM 
-gm1  g01+g03 /2 
 sC+g01+g05  gm1+g01+g03 /2  -gm1g01
pCOM  
g05
C
-
g01+g03 /2
sC+g05
And this is different from the
difference-mode pole
But the common-mode gain tells
little, if anything, about the CMFB
Mathematics behind CMFB
(consider an example that needs a CMFB)
g05
A COM
g +g /2
- 01 03
sC+g05
gm1
2
A DIFF =
sC+g01+g05
g
pCOM   05
C
•
•
•
•
•
•
•
VO1
V1
pDIFF = -
VO2
V2
gm2VGS2
gm1VGS1
VGS1
g01
g02
C1
g03/2
-
•
g04
C2
g03/2
g01+g05
C
Difference-mode analysis completely hides all information about commonmode
This also happens in simulations
Common-mode analysis completely hides all information about differencemode
This also happens in simulations
Difference-mode poles may move into RHP with FB so compensation is
required for stabilization (or proper operation)
Common-mode poles may move into RHP with FB so compensation is
required for stabilization (or proper operation)
Difference-mode simulations tell nothing about compensation requirements
for common-mode feedback
Common-mode simulations tell nothing about compensation requirements
for difference-mode feedback
VGS2
Mathematics behind CMFB
(consider an example that needs a CMFB)
g05
A COM
g +g /2
- 01 03
sC+g05
gm1
2
A DIFF =
sC+g01+g05
g
pCOM   05
C
•
•
VO1
V1
pDIFF = -
VO2
V2
gm2VGS2
gm1VGS1
VGS1
g01
g02
C1
g03/2
-
•
g04
C2
g03/2
g01+g05
C
Common-mode and difference-mode gain expressions often include same
components though some may be completely absent in one or the other
mode
Compensation capacitors can be large for compensating either the
common-mode or difference-mode circuits
Highly desirable to have the same compensation capacitor serve as the
compensation capacitor for both difference-mode and common-mode
operation
– But tradeoffs may need to be made in phase margin for both modes if this is
done
•
Better understanding of common-mode feedback is needed to provide good
solutions to the problem
VGS2
Mathematics behind CMFB
(consider an example that needs a CMFB)
g05
g05
g04
VO1
V1
VO2
V2
gm2VGS2
gm1VGS1
VGS1
g01
g02
C1
C2
VGS2
VOC
VCOM
g03/2
g03/2
gm1VGS1
g01
VGS1
C
VS
g03/2
Standard small-signal common-mode half circuit
VOC  sC+g01+g05  +gm1  VCOM -VS   0
Note there is a single-pole in this circuit
VS  g01+g03 /2 -gm1  VCOM -VS   VOCg01
A COM 
-gm1  g01+g03 /2 
 sC+g01+g05  gm1+g01+g03 /2  -gm1g01
pCOM  
g05
C
-
g01+g03 /2
sC+g05
And this is different from the
difference-mode pole
But the common-mode gain tells
little, if anything, about the CMFB
Common-Mode and Difference-Mode Issues
Overall poles are the union of the common-mode and difference mode poles
Separate analysis generally require to determine common-mode and differencemode performance
Some amplifiers will need more than one CMFB
Common-mode offset voltage
VDD
M5
VO1
V0XX
VCOFF
C1
VC1
M1
VYY
VB1
M4
V0XX
M2
VO2
VC1
C2
M3
Definition: The common-mode offset voltage is the voltage that must be
applied to the biasing node at the CMFB point to obtain the desired
operating point at the stabilization node
Common-mode offset voltage
VDD
Consider again the Common-mode half circuit
M5
VDD
VO1
V0XX
VCOFF
C1
M1
VC1
VB1
M4
V0XX
M2
VO2
VC1
M4
VXX
VYY
VO2
VCOFF
M2
VC1
C2
M3
VYY
M3
M’3
M’3
M’3
There are three common-mode inputs to this circuit !
The common-mode signal input is distinct from the input that is affected by VCOFF
The gain from the common-mode input where VFB is applied may be critical !
C2
Common-mode gains
VDD
VDD
M5
VO1
VC2
V0XX
C1
M4
VC1
VYY
V02
VC1
g01+g03 /2
sC+g05
V02
gm5
VC2
sC+g05
V
g /2
 02 - m3
VC3
sC+g05
A COM2 
A COM3
-
-
M2
VC1
M3
g01+g03 /2
 IT
1


g05
 IT / 2
2
VC3
A COM20
A COM 
VB1
VO2
C
A COM0
M’3
M1
VC1
VO2
M2
VCOFF
M4
V0XX
A COM30
-
gm5
2I / V
4
  T EB 5  
g05
 IT / 2
VEB 5
2IT
/2
gm3 /2
VEB3
2

=
g05
IT /2
 VEB3
Although the common-mode gain ACOM0 is very
small, AC0M20 is very large!
Shift in V02Q from VOXX is the product of the
common-mode offset voltage and ACOM20
C2
Effect of common-mode offset voltage
VDD
VDD
M5
VO1
V0XX
C1
VC2
VC1
M4
VC3
M1
VYY
VB1
M4
V0XX
M2
VO2
VC1
C2
M3
VO2
VCOFF
VB1
VCOFF
M2
VC1
M’3
C2
A COM20
How big is ACOM20?
4
VEB 5
V02 = ACOM20 VCOFF
How much change in V02 is acceptable?
How big if VCOFF?

(assume e.g. 50mV)
(similar random expressions for VOS, assume, e.g. 25mV)
(that due to process variations even larger)
(if λ=.01, VEB=.2, ACOM20=2000)
If change in V02 is too large, CMFB is needed
(50mV <? 2000x25mV)
How much gain is needed in the CMFB
amplifier?
VDD
VFB
M3
M4
VOUT
VOUT
VIN
M1
M2
CMFB
Circuit
VIN
CL
CL
VOXX
VB2
M9
CMFB Block
VO1
VAVG
Averager
A
VFB
VO2
VOXX
CMFB must compensate for VCOFF
Want to guarantee
V02Q -V0XX < ΔVOUT-ACCEPTABLE
This is essentially the small-signal output with a small-signal input of VCOFF
How much gain is needed in the CMFB
amplifier?
VDD
VFB
M3
M4
VOUT
VOUT
VDD
VIN
M1
M2
CMFB
Circuit
VIN
CL
CL
VOXX
VC1
VB2
M4
VO2
VCOFF
M2
VC1
VAVG
C2
A
VFB
VOXX
VC3
M9
Want to guarantee
M’3
V02Q -V0XX < ΔVOUT-ACCEPTABLE
The CMFB Loop
Do a small-signal analysis, only input is VCOFF
V02 =  V02 A+VCOFF  A COM2
V02 =VCOFF
A COM2
1-AA COM2
V0UT-ACCEPTABLE =VCOFF
A COM2
1-AA COM2
How much gain is needed in the CMFB
amplifier?
VDD
VFB
VDD
M3
M4
VOUT
VOUT
VC1
VIN
CMFB
Circuit
VIN
CL
VOXX
VO2
VCOFF
VC1
VAVG
A
C2
VOXX
VC3
M2
CL
M4
M2
M1
M’3
VFB
VB2
M9
V0UT-ACCEPTABLE =VCOFF
A COM2
1-AA COM2
The CMFB Loop
• This does not require a particularly large gain
• This is the loop that must be compensated since A and ACOMP2 will be
frequency dependent
• Miller compensation capacitor for compensation of differential loop will often
appear in shunt with C2
• Can create this loop without CM inputs on fully differential structure for
simulations
• Results extend readily to two-stage structures with no big surprises
CMFB Circuits
Several (but not too many) CMFB circuits exist
Can be classified as either continuous-time or discrete-time
VDD
IB
Vo+
IB
VOXX
V01
N2
N1
M1
VFB
M2
M3
M5
VSS
M7
M6
VSS
M4
V02
CS
V01
N1
Vo-
N2
C1 C1
N2
CS
N2
VFB
N1
N1
V02
End of Lecture 24