Download The complexity of the Separable Hamiltonian

André Chailloux, Université Paris 7 and UC Berkeley
Or Sattath, the Hebrew University
QIP 2012


Merlin(prover) is all powerful, but malicious.
Arthur(verifier) is skeptical, and limited to BQP.
A problem LQMA if:
 xL ∃| that Arthur accepts w.h.p.
 xL  ∀| Arthur rejects w.h.p.
|𝜓〉


The same as QMA, but with 2 provers, that do
not share entanglement.
Similar to interrogation of suspects:
|𝝍𝑨 〉
⊗
|𝝍𝑩 〉
QMA(2) has been studied extensively:
 There are short proofs for NP-Complete problems
in QMA(2)[BT’07,ABD+’09,Beigi’10,LNN’11].
 Pure N-representability  QMA(2)
[LCV’07], not known to be in QMA.
 QMA(k) = QMA(2) [HM’10].
 QMA ⊆PSPACE, while the best upper-bound is
QMA(2) ⊆ NEXP [KM’01].
[ABD+’09] open problem:
“Can we find a natural QMA(2)-complete problem?”
We introduce a natural candidate for a QMA(2)completeness: Separable version of LocalHamiltonian.
Theorem 1: Separable Local Hamiltonian is
QMA-Complete!
Theorem 2: Separable Sparse Hamiltonian
Local Hamiltonian problem:
isThe
QMA(2)-Complete.
Given 𝐻 = 𝑖 𝐻𝑖 , (𝐻𝑖 acts on k qubits)
A
is sparse
each row has at
is Hamiltonian
there a state𝐻
with
energyif <a
most
or all polynomial
states have non-zero
energy > bentries.
?



Problem: Given 𝐻 = 𝑖 𝐻𝑖 , and a partition of
the qubits, decide whether there exists a
separable state with energy at most a or all
separable states have energies above b?
The witness: the separable state with energy
below a.
The verification: Estimation of the energy.


Theorem 1: Separable Local HamiltonianQMA.
First try: the prover provides the witness, and the
verifier checks that it is not entangled. We don’t know
how.
Theorem 1: Separable Local HamiltonianQMA.
Second try: The prover sends the classical description of
all k local reduced density matrices of the A part and of
the B part separately .
 The prover proves that there exists a state 𝜌 which is
consistent with the local density matrices.
 The state 𝜌 can be entangled, but if 𝜌 exists, then also
𝜌′ = 𝜌 𝐴 ⊗ 𝜌𝐵 exists, where 𝜌 𝐴 = 𝑡𝑟𝐵 (𝜌), and similarly
𝜌𝐵 .
 The verifier uses the classical description to calculate
the energy:
𝑇𝑟 𝐻𝜌′ = 𝑖 𝑇𝑟(𝐻𝑖 𝜌′)


Consistensy of Local Density Matrices
Problem (CLDM):
 Input: density matrices 𝜎1 , … , 𝜎𝑚 over k qubits and
sets 𝐴1 , … , 𝐴𝑚 ⊂ {1, … , 𝑛}.
 Output: yes, if there exists an n-qubit state 𝜌 which
is consistent: ∀𝑖 ≤ 𝑚, 𝜌 𝐴𝑖 = 𝜎𝑖 . No, otherwise.
Theorem[Liu`06]: CLDM ∈ QMA.
The prover sends:
a) Classical part, containing the reduced density
matrices of the A part, and the B part.
b) A quantum proof for the fact that such a state 𝜌
exists.
 The verifier:
a) classically verifies that the energy is below the
threshold a, assuming that the state is
𝜌′ = 𝜌 𝐴 ⊗ 𝜌𝐵 .
b) verifies that there exists such a state 𝜌 using the
CLDM protocol.

Separable Sparse Hamiltonian is
QMA(2)-Complete.


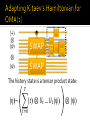
Given a quantum circuit Q, and a witness |𝜓〉,
the history state is:
𝜂𝜓 ∼ 𝑇𝑡=0 𝑡 ⊗ 𝜓𝑡 ,
𝜓𝑡 ≡ 𝑈𝑡 … 𝑈1 𝜓 .
Kitaev’s Hamiltonian gives an energetic penalty
to:
 states which are not history states.
 history states are penalized for Pr(Q rejects |𝜓〉)

Only if there exists a witness which Q accepts
w.h.p., Kitaev’s Hamiltonian has a low energy
state.
What happens if we use Kitaev’s Hamiltonian
for a QMA(2) circuit, and allow only separable
witnesses?
Problems:
 Even if 𝜓 = 𝜓𝐴 ⊗ |𝜓𝐵 〉, then |𝜓𝑡 〉 is
typically not separable.
 Even if ∀𝑡 |𝜓𝑡 〉 is separable , |𝜂𝜓 〉 is typically
entangled.
For this approach to work, one part must be
fixed during the entire computation.



We need to assume that one part is fixed
during the computation.
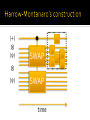
Aram Harrow and Ashley Montanaro have
shown exactly this!
Thm: Every QMA(k) verification circuit can be
transformed to a QMA(2) verification circuit
with the following form:
|+〉
⊗
|𝜓〉
SWAP
⊗
|𝜓〉
SWAP
time
|+〉
⊗
|𝜓〉
SWAP
⊗
SWAP
|𝜓〉
The history state is a tensor product state:
𝑇
𝜂~
𝑡 ⊗ 𝑈𝑡 … 𝑈1 𝜓
𝑡=0
⊗ |𝜓〉

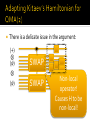
There is a delicate issue in the argument:
|+〉
⊗
|𝜓〉
SWAP
⊗
|𝜓〉
SWAP
Non-local
operator!
Causes H to be
non-local!
Control-Swap over multiple qubits is
sparse.
 Local & Sparse
Hamiltonian common
1
properties: 1

1
C-SWAP=
Compact description
Simulatable
Hamiltonian in QMA
Local Sparse
1
.
1
1
1
Separable Hamiltonian in QMA(2)
1

The instance that we constructed is local,
except one term which is sparse.

Theorem 2: Separable Sparse Hamiltonian is
QMA(2)-Complete.
Known results: Local Hamiltonian & Sparse
Hamiltonian are QMA-Complete.
 A “reasonable” guess would be that both their
Separable version are either QMA(2)-Complete, or
QMA-Complete, but it turns out to be wrong*.
 Separable Local Hamiltonian is QMAComplete.
 Separable Sparse Hamiltonian is QMA(2)Complete.

* Unless QMA = QMA(2).
Can this help resolve whether Pure NRepresentability is QMA(2)-Complete or not?
 QMA vs. QMA(2) ?


We would especially like to thank Fernando
Brandão for suggesting the soundness proof
technique.
Similar to CLDM, but with the additional
requirement that the state is pure (i.e. not a mixed
state).
 In QMA(2): verifier receives 2 copies, and estimates
the purity using the swap test:
Pr(𝜎 ⊗ 𝜏 passes the swap test) = 𝑇𝑟 𝜎𝜏 ≤ 𝑇𝑟(𝜎 2 ).



Theorem 2: Separable Sparse Hamiltonian is
QMA(2)-Complete.
Why not: Separable Local Hamiltonian is
QMA(2)-Complete?
SWAP
SWAP


If we use the local implementation of C-SWAP, the
history state becomes entangled.
Only Seems like a technicality.