* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download The complexity of the Separable Hamiltonian
Density functional theory wikipedia , lookup
Perturbation theory wikipedia , lookup
Quantum decoherence wikipedia , lookup
Ising model wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Compact operator on Hilbert space wikipedia , lookup
Quantum teleportation wikipedia , lookup
Path integral formulation wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
BRST quantization wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Scalar field theory wikipedia , lookup
Noether's theorem wikipedia , lookup
Density matrix wikipedia , lookup
Tight binding wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Quantum entanglement wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Canonical quantum gravity wikipedia , lookup
Canonical quantization wikipedia , lookup
André Chailloux, Université Paris 7 and UC Berkeley
Or Sattath, the Hebrew University
QIP 2012
Merlin(prover) is all powerful, but malicious.
Arthur(verifier) is skeptical, and limited to BQP.
A problem LQMA if:
xL ∃| that Arthur accepts w.h.p.
xL ∀| Arthur rejects w.h.p.
|𝜓〉
The same as QMA, but with 2 provers, that do
not share entanglement.
Similar to interrogation of suspects:
|𝝍𝑨 〉
⊗
|𝝍𝑩 〉
QMA(2) has been studied extensively:
There are short proofs for NP-Complete problems
in QMA(2)[BT’07,ABD+’09,Beigi’10,LNN’11].
Pure N-representability QMA(2)
[LCV’07], not known to be in QMA.
QMA(k) = QMA(2) [HM’10].
QMA ⊆PSPACE, while the best upper-bound is
QMA(2) ⊆ NEXP [KM’01].
[ABD+’09] open problem:
“Can we find a natural QMA(2)-complete problem?”
We introduce a natural candidate for a QMA(2)completeness: Separable version of LocalHamiltonian.
Theorem 1: Separable Local Hamiltonian is
QMA-Complete!
Theorem 2: Separable Sparse Hamiltonian
Local Hamiltonian problem:
isThe
QMA(2)-Complete.
Given 𝐻 = 𝑖 𝐻𝑖 , (𝐻𝑖 acts on k qubits)
A
is sparse
each row has at
is Hamiltonian
there a state𝐻
with
energyif <a
most
or all polynomial
states have non-zero
energy > bentries.
?
Problem: Given 𝐻 = 𝑖 𝐻𝑖 , and a partition of
the qubits, decide whether there exists a
separable state with energy at most a or all
separable states have energies above b?
The witness: the separable state with energy
below a.
The verification: Estimation of the energy.
Theorem 1: Separable Local HamiltonianQMA.
First try: the prover provides the witness, and the
verifier checks that it is not entangled. We don’t know
how.
Theorem 1: Separable Local HamiltonianQMA.
Second try: The prover sends the classical description of
all k local reduced density matrices of the A part and of
the B part separately .
The prover proves that there exists a state 𝜌 which is
consistent with the local density matrices.
The state 𝜌 can be entangled, but if 𝜌 exists, then also
𝜌′ = 𝜌 𝐴 ⊗ 𝜌𝐵 exists, where 𝜌 𝐴 = 𝑡𝑟𝐵 (𝜌), and similarly
𝜌𝐵 .
The verifier uses the classical description to calculate
the energy:
𝑇𝑟 𝐻𝜌′ = 𝑖 𝑇𝑟(𝐻𝑖 𝜌′)
Consistensy of Local Density Matrices
Problem (CLDM):
Input: density matrices 𝜎1 , … , 𝜎𝑚 over k qubits and
sets 𝐴1 , … , 𝐴𝑚 ⊂ {1, … , 𝑛}.
Output: yes, if there exists an n-qubit state 𝜌 which
is consistent: ∀𝑖 ≤ 𝑚, 𝜌 𝐴𝑖 = 𝜎𝑖 . No, otherwise.
Theorem[Liu`06]: CLDM ∈ QMA.
The prover sends:
a) Classical part, containing the reduced density
matrices of the A part, and the B part.
b) A quantum proof for the fact that such a state 𝜌
exists.
The verifier:
a) classically verifies that the energy is below the
threshold a, assuming that the state is
𝜌′ = 𝜌 𝐴 ⊗ 𝜌𝐵 .
b) verifies that there exists such a state 𝜌 using the
CLDM protocol.
Separable Sparse Hamiltonian is
QMA(2)-Complete.
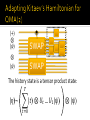
Given a quantum circuit Q, and a witness |𝜓〉,
the history state is:
𝜂𝜓 ∼ 𝑇𝑡=0 𝑡 ⊗ 𝜓𝑡 ,
𝜓𝑡 ≡ 𝑈𝑡 … 𝑈1 𝜓 .
Kitaev’s Hamiltonian gives an energetic penalty
to:
states which are not history states.
history states are penalized for Pr(Q rejects |𝜓〉)
Only if there exists a witness which Q accepts
w.h.p., Kitaev’s Hamiltonian has a low energy
state.
What happens if we use Kitaev’s Hamiltonian
for a QMA(2) circuit, and allow only separable
witnesses?
Problems:
Even if 𝜓 = 𝜓𝐴 ⊗ |𝜓𝐵 〉, then |𝜓𝑡 〉 is
typically not separable.
Even if ∀𝑡 |𝜓𝑡 〉 is separable , |𝜂𝜓 〉 is typically
entangled.
For this approach to work, one part must be
fixed during the entire computation.
We need to assume that one part is fixed
during the computation.
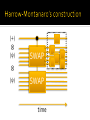
Aram Harrow and Ashley Montanaro have
shown exactly this!
Thm: Every QMA(k) verification circuit can be
transformed to a QMA(2) verification circuit
with the following form:
|+〉
⊗
|𝜓〉
SWAP
⊗
|𝜓〉
SWAP
time
|+〉
⊗
|𝜓〉
SWAP
⊗
SWAP
|𝜓〉
The history state is a tensor product state:
𝑇
𝜂~
𝑡 ⊗ 𝑈𝑡 … 𝑈1 𝜓
𝑡=0
⊗ |𝜓〉
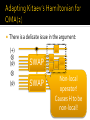
There is a delicate issue in the argument:
|+〉
⊗
|𝜓〉
SWAP
⊗
|𝜓〉
SWAP
Non-local
operator!
Causes H to be
non-local!
Control-Swap over multiple qubits is
sparse.
Local & Sparse
Hamiltonian common
1
properties: 1
1
C-SWAP=
Compact description
Simulatable
Hamiltonian in QMA
Local Sparse
1
.
1
1
1
Separable Hamiltonian in QMA(2)
1
The instance that we constructed is local,
except one term which is sparse.
Theorem 2: Separable Sparse Hamiltonian is
QMA(2)-Complete.
Known results: Local Hamiltonian & Sparse
Hamiltonian are QMA-Complete.
A “reasonable” guess would be that both their
Separable version are either QMA(2)-Complete, or
QMA-Complete, but it turns out to be wrong*.
Separable Local Hamiltonian is QMAComplete.
Separable Sparse Hamiltonian is QMA(2)Complete.
* Unless QMA = QMA(2).
Can this help resolve whether Pure NRepresentability is QMA(2)-Complete or not?
QMA vs. QMA(2) ?
We would especially like to thank Fernando
Brandão for suggesting the soundness proof
technique.
Similar to CLDM, but with the additional
requirement that the state is pure (i.e. not a mixed
state).
In QMA(2): verifier receives 2 copies, and estimates
the purity using the swap test:
Pr(𝜎 ⊗ 𝜏 passes the swap test) = 𝑇𝑟 𝜎𝜏 ≤ 𝑇𝑟(𝜎 2 ).
Theorem 2: Separable Sparse Hamiltonian is
QMA(2)-Complete.
Why not: Separable Local Hamiltonian is
QMA(2)-Complete?
SWAP
SWAP
If we use the local implementation of C-SWAP, the
history state becomes entangled.
Only Seems like a technicality.