* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Low-Power Oscillator Design - Courses
Operational amplifier wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Surge protector wikipedia , lookup
Time-to-digital converter wikipedia , lookup
Opto-isolator wikipedia , lookup
Electronic engineering wikipedia , lookup
Power MOSFET wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Standing wave ratio wikipedia , lookup
Power electronics wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
Regenerative circuit wikipedia , lookup
Rectiverter wikipedia , lookup
Phase-locked loop wikipedia , lookup
Radio transmitter design wikipedia , lookup
Index of electronics articles wikipedia , lookup
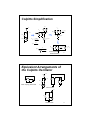
Low-Power Oscillator Design Presented by Ken Pedrotti University of California Santa Cruz, CA 95064 831-459-1229 Phone 831-459-4829 FAX [email protected] Notes for Mead course on Low-Power Oscillator Design Santa Cruz, CA 95064 1 2 Outline •A quick history of accurate time keeping •Analogies to Electrical Oscillators •Oscillator Fundamentals •Amplitude Limiting •Phase Noise and Figure of Merit •Colpitts Oscillator •Single Transistor Oscillators •Differential Oscillators •Low Power, Low Phase Noise Differential Oscillator Design Example •Bonus Material •Rotary Traveling Wave Oscillators 3 Oscillator fundamentals Characterized principally by its natural frequency and how wide a range of frequencies it will respond to resonantly its resonance response (Q or Quality Factor) High Q implies oscillator puts out a narrow range of frequencies and is difficult to “disturb” Q=2π Energy of system f ≈ R Energy lost per period Δf 4 Ancient Oscillator: Verge and Foliot Verge and Foliot •Period directly dependent on power source •No resonator •Low Energy Storage •Accuracy Measured in Hours per day •Electrical Analog:Ring Oscillators From Horology Room, British Museum, Fusees and Escapements 5 Ring Oscillator f0 = n τ pLH 1 + τ pHL N must be odd to insure oscillation For startup the small signal gain of each stage viewed as an amplifier must be greater than 1. 6 Wien bridge oscillator C1 If Ra R1 R2 C2 R1 = R2 + C1 = C2 - Ra = 2 Rb Rb The the bridge will be in balance at RC RLC ω0 = 1 RC Amplitude Phase Vin will then be in phase with Vout so we have positive feedback around the loop. The loop gain will be >1 as long as Ra>2Rb 7 Major Advance Add a Resonator Pendulum added by Christian Huygens •The pendulum acts as a resonator and energy storage device •Less sensitivity to the power source •Power variation results in amplitude change but little change in period •Pendulum still in constant contact with power source, this is bad Electrical Analogy •LC oscillator at low amplitude (constant power input) 8 Impulsing a Pendulum:Anchor Escapement •Greatly improved on the Verge •Allowed much smaller amplitude swings, pendulum became more isochronous •Allowed longer slower moving pendulums, less loss: higher Q •Disadvantage still highly coupled to Power source so noise in gearing and spring directly leads to phase noise in the resonator. •Pendulum is never swinging entirely free 9 www.angelfire.com/ut/horology/escapement.html Deadbeat Escapement Contact surfaces curved to better isolate the pendulum from the variable power source First to separate the locking and impulsing function 10 Impulsing a Pendulum:Gravity Escapement With the gravity escapement the resonator was detached from the power source. One arm unlocks the escape wheel which rather than impulsing the pendulum directly raises the arm that is not in contact. The impulse is provided when the arm ends at a lower height than when it starts. Impulse supplied at the wrong time i the cycle Electrical lesson: isolate your drive from the power source. 11 Riefler Clock Invar Pendulum Rod (Low Thermal Expansion) Pendulum highly detached, impulsed solely through suspension point. Evacuate housing for low loss, high Q and environmental isolation Powered using a remontoire, a small weight that was rewound by an electric motor every 30 sec. Accuracy 10 ms/day Electrical Analogy: Careful attention to isolate from PVT, High Q, optimal impulsing time. 12 Demise of the Pendulum Balance Wheels and Springs let to a truly harmonic resonator. This shifted design emphasis to the escapement and constancy of the power train. 13 Summary: Your first clock will be a thermometer Your next clock will be a barometer And if you are really good your final clock will be a seismometer And what does this mean for oscillators? A good design will •Use a high Q resonator •Interact minimally with the power source •Be impulsed at the optimum time •Tolerate PVT variations 14 Over Damped Oscillator R Vout G H(ω) H(ω) +900 ω0 jω -900 σ V = − LC d 2V dV − LGl dt 2 dt LCs 2 + LGs + 1 = 0 15 Under damped Oscillator R G Vout H(ω) H(ω) +900 ω0 jω -900 LC d 2V dV − LGg +V = 0 dt 2 dt LCs 2 − LGg s + 1 = 0 σ 16 Critically Damped R G Vout H(ω) ω0 H(ω) +900 L C jω -900 LC d 2V +V = 0 dt 2 Position σ Velocity Acceleration LCs 2 + 1 = 0 17 Van der Pol Approximation L C L C Gl L C Gl LC d 2V +V = 0 dt 2 LC d 2V dV + LGl +V = 0 2 dt dt F(v) LCs 2 + 1 = 0 LCs 2 + LGs + 1 = 0 LC d 2V d + L [GlV + F (V )] + V = 0 2 dt dt LC d 2V d + L ⎣⎡GlV − GgV + GsatV 3 ⎦⎤ + V = 0 dt 2 dt F(v) V F (V ) = −GgV + GsatV 3 18 Amplitude limitation • Directly through the gain saturation • Indirectly via a bias shift As amplitude grows eventually this term wins Loss term LC d 2V d + L ⎡⎣GlV − GgV + GsatV 3 ⎤⎦ + V = 0 dt 2 dt Gain term • Startup Condition: L (Gg − Gl ) ≥ 1 C V (t ) = A exp( 1 L 1 (Gg − Gl )t ) cos( t) 2 C LC 19 HP 200C Audio Amplifier 1943 Catalog Copy The lamp served as a non-linear resistance that was used to stabilize the output amplitude http://oak.cats.ohiou.edu/~postr/bapix/HP200C.htm 20 Oscillator Figure of Merit ⎛ω ⎞ 1 FOM = ⎜ o ⎟ ⎝ ω ⎠ L(ω )P ωo = Oscillator Center Frequency ω = Offset from Center Frequency L(ω ) = Phase noise at offset ω from center frequency P = Power in mW So for a low power design what we mean is low phase noise for a given power 21 Oscillator Phase Noise Phase Noise: Caused by fluctuations in the oscillator Qualified by sideband power over carrier power (unit dBc/Hz): ⎡P (w + Δw,1Hz )⎤ Ltotal {Δw} = 10 log ⎢ sideband o ⎥ Pcarrier ⎣ ⎦ α Pnoise 1/f noise L{Δ w} 1/f3 Thermal noise in the oscillator Thermal noise in the external circuit eg. 50 Ohm line 1/f2 ω1/ f 3 α Ps Log(f) 22 Leeson’s Model L{Δ w} 2 ⎛ 2 FkT ⎡ ⎛ ω ⎞ ⎤ ⎛ ω1/ f 3 0 ⎢1 + ⎜ L{Δw} = 10 log ⎜ ⎟ ⎥ ⎜⎜1 + ⎜ Ps ⎢ ⎝ 2QL Δω ⎠ ⎥ ⎝ Δω ⎣ ⎦ ⎝ PS = Signal power 1/f3 ω0 = Oscillation Frequency Δω = Frequency offset from the carrier 1/f2 ω1/ f ⎞⎞ ⎟⎟ ⎟ ⎠ ⎟⎠ QL = Quality factor of the fully loaded resonator 3 Log(f) F= Device excess noise factor (empirical) 1 1 ω1/ f 3 = Corner frequency between 3 and 2 regions (also empirical) f f Leeson’s model is commonly used to represent the phase noise in oscillators. It does capture the empirical behavior but relys on “fitting factors” that are not in general known apriori. This model is based on a Linear Time Invarient (LTI) analysis with the empirical inclusion of the 1/f noise which cannot be handled by an LTI analysis D.B. Leeson, “ A Simple Model of Feed-back Oscillator Noise Spectrum”, Proc. IEEE, vol. 54 , pp. 329-330, Feb. 1966. J. Craninckx, M. Steyaert, “ Low-noise Voltage Controlled Oscillators Using Enhanced LC-tanks ”, IEEE Trans. Circuits Syst.-II, vol. 42 , 23 pp. 794-904, Dec. 1995. Theory Background of Phase Noise Model • Oscillator is a time-variant system! • Traditional phase noise model (Leeson’s model) based on Linear Time Invariant (LTI) theory does not apply for quantitative prediction. • Linear Time Variant Theory introduced by Hajimiri, known in the Horology community since 1827*. *Airy, Sir Georg Biddle, Cambridge Philosophical Transactions, 1827, Vol. 3, Part 1, pp. 105-128 Perturbations at different times in a cycle create different amounts of phase noise & amplitude noise 24 Linear Time Varying (LTV) Theory Impulse Sensitivity Function (ISF) • Only depends on wave shape • Unitless • Periodic • Indicate the sensitivity to noise injection Sinewave oscillator Squarewave oscillator 25 Phase Noise Predicted by LTV • White noise induced L{Δ w} ⎛ Γ 2 i 2 / Δf ⎞ ⎟ L{Δw} = 10 log⎜ 2rms n ⎜ q max 2 ⋅ Δw 2 ⎟ ⎠ ⎝ 1/f3 • Flicker noise induced 1/f2 ⎛ c 2 i 2 / Δf w1 / f ⎞ ⎟ L{Δw} = 10 log⎜ 20 n ⎜ q max 2 ⋅ Δw 2 Δw ⎟ ⎝ ⎠ Log(f) Typical phase noise log-log plot 2 Γrms --rms value of ISF Fourier expansion Co --DC value of ISF Fourier expansion q max = c node ⋅ Vmax 26 Figure of Merit ⎛⎛ f ⎞ 1 FOM = 10 log ⎜ ⎜ o ⎟ ⎜ ⎝ Δf ⎠ L {Δf } Ps ⎝ f o = Oscillator frequency 2 ⎞ ⎟ ⎟ ⎠ Δf = Deviation for center frequency at which phase noise is measured L {Δf } = Phase noise spectral density Δf from the oscillator frequency Ps = Oscillator power in mW α Pnoise 2 2 FkT ⎡ ⎛ ω0 ⎞ ⎤ ⎛ ω1/ f 3 ⎞ ⎢1 + ⎜ ⎟ ⎟ ⎥ ⎜⎜1 + Ps ⎢ ⎝ 2QL Δω ⎠ ⎥ ⎝ Δω ⎟⎠ ⎣ ⎦ at high frequency L{Δω} = L{Δw} ≈ 2 FkT Ps L{Δw} ∝ FkT QL ⎛ ω0 ⎞ ⎜ ⎟ ⎝ 2QL Δω ⎠ α Ps 2 2 ⎛ f0 ⎞ 1 ⎜ ⎟ ⎝ Δf ⎠ Ps 27 Colpitts VDD L Vbias C1 C2 Edwin H. Colpitts 28 Capacitive Transformer VDD L C1 Vbias L C2 C1 C2 C EQ = C1C2 C1 + C2 R 1 L η= η2 Ceq C1 C1 + C2 29 Inductor Loss Transformation Rs LP RP LS ( ) RP = RS Q 2 + 1 ≅ RS Q 2 = (ω0 LS ) 2 RS ⎛ Q2 + 1 ⎞ LP = LS ⎜ ⎟ ≅ LS 2 ⎝ Q ⎠ where Q= ω0 LS RS = RP ω0 LS 30 R Colpitts Simplification VDD VDD VDD L Vout RP L Ceq 1 1 η 2 gm Vbias Ceq C1 C2 C EQ = η= 1 1 L η 2 gm Vbias Vout + C1C2 C1 + C2 || RP − g mηVout g mηVout - C1 C1 + C2 Ceq 1 f0 = 2π L C1C2 C1 + C2 L 1 1 η 2 gm Small Signal ModelUseful for Startup || RP 31 Equivalent Arrangements of the Colpitts Oscillator VDD L Vbias C1 Basic Topology without bias C2 Vdd Common Gate VDD C1 L C2 Common Drain 32 − g mηVout Colpitts Impulsing Resonator Voltage Amplitude regulation mechanism is due to a bias shift on C2 as the oscillation grows. VDD L The amplitude is somewhat difficult to predict, best attempted using the Describing Function Method.* Vbias C1 C2 The impulse timing occurs at the point in the cycle that the circuit is least sensitive to the drain noise. Drain Current See for example T. H Lee, The Design of CMOS Radio-Frequency Integrated Circuits, Second Edition 2003 33 Clapp Oscillator VDD L2 L1 VDD C0 Vbias C1 L C1 C0 C2 Essentially a Colpitts oscillator with an additional capacitor in series with the inductor. Often preferred for VCOs C2 Clapp James K Clapp, 1948 In a Colpitts using either of the divider capacitors to tune the oscillator results in a variable feedback voltage. Here using C0 for tuning decouples the two functions. 34 Hartley Oscillator Colpitts Hartley Ralph V. L. Hartley 1915 Electrical Dual of the Colpitts Oscillator f0 = Inductive divider provides feedback signal Best tuned using a variable capacitor 1 2π C ( L1 + L2 ) 35 Differential Oscillators VDD VDD VDD VDD Vbias Vbias Vbias − Often preferred for modern integrated applications due to greater noise immunity, inverse phases 2 gm Better PVT Performance 36 Low Phase Noise Design Design Example VDD 12 independent design variables: Mosfets: Wn, Ln, Wp, Lp (Assuming symmetry) Vtune Cload Inductor: metal width W, metal spacing S, number of turns N, lateral dimension D Cload Maximum and minimum varactor values Cv,max, Cv,min Bias Current I Vbias How do we optimize for best Figure of Merit? Put otherwise: for a given amount of power how do we get the lowest phase noise? After D.H. Ham Chapt 18, “Tradeoffs in Analog Design” pp. 517-549 37 Inductor Model w Inter-turn Capacitance Series Resistance CS L D RP CP RS CP RP Capacitance and S Leakage to Substrate 38 Design Constraints Power Constraint I ≤ I Max Need a large enough swing to reduce phase noise Vsw = IRtan k ,max ≥ Vsw,min Power is VddImax VDD 1 ≤ ωmax LCmin Required Tuning range Vtune Cload Cload 1 ≥ ωmin LCmax Startup constraint, small signal gain must exceed loss g≥ Maximum inductor dimension, area constraint D ≤ Dmax α min Vbias Rtan k ,max 39 Oscillator Simplicfication Cload VDD Cload Cload Spiral inductors Cs+Cp Cs+Cp Vtune Input Capacitance Of Output drivers L RS L RS CV RV RV Tuning Varactors Cload Cn+Cpm Vbias CV Cn+Cpm -(gm,n+ gm,p) -(gm,n+ gm,p) go,n+ go,p go,n+ go,p MOS Transistors 40 Oscillator Simplicfication VDD ½(Cs+Cp+ Cn+Cp+Cload) Vtune Cload Cload gL/2 Spiral inductors 2L L Vbias gV/2 Cload Input Capacitance Of Output drivers Cload Spiral inductors Cs+Cp Cs+Cp L RS L CV RV RV Cn+Cpm RS Tuning Varactors CV Cn+Cpm -(gm,n+ gm,p) -(gm,n+ gm,p) go,n+ go,p go,n+ go,p Tuning Varactors C CV/2 gres MOS Transistors -2(gm,n+ gm,p) -g 2(go,n+ go,p) MOS Transistors g res = 1 ( g o ,n + g o , p + g v + g L ) 2 41 Objective Function • Objective is to minimize the phase noise subject to the given constraints L{Δf } = Means that the MOSFET drain noise will be dominant, so we consider only that term ⎛ in2 ∑ ⎜⎜ 2 ⋅ Δf n ⎝ 2 ⎞ 2 Γ rms ,n ⎟ ⎟ ⎠ id2 = 2kT γ ( g dn + g dp ) Δf qmax = Turns out that the start up condition that g>gres 1 1 2 8πΔf qmax Vsw,max C = Vsw,max Lω 2 ⎡ ⎤ f 4 L2 I 1 1 ⎥ 2 2 L{Δf } = 16π 2 kT γ ⎢ + L E ⎢⎣ ( n sat ,n ) ( Lp Esat , p ) ⎥⎦ Δf Vsw,max 1 2 Γ rms ,n 2 gd 0 = 2 I drain (L E ) n sat , n 42 Objective Function Simplification The Phase noise Expression can be simplified to show the portions that depend on our design parameters. In the current limited regime we can decrease the phase noise by increasing the current ⎡ ⎤ f 4 L2 I 1 1 ⎥ 2 2 L{Δf } = 16π 2 kT γ ⎢ + ⎢⎣ ( Ln Esat , n ) ( L p Esat , p ) ⎥⎦ Δf Vsw,max Vsw,max = I g res Current Limited Vsw,max = Vsup ply Voltage Limited ⎡ ⎤ f4 1 1 ⎥ 2 + ⎢⎣ ( Ln Esat ,n ) ( L p Esat , p ) ⎥⎦ Δf 2 η L2 g res Current Limited L{Δf } = I η = 16π 2 kT γ ⎢ Once the supply limits the voltage swing then further current increases actually increase the phase noise The optimum point to operate is thus on the border between the current and voltage limited regimes L{Δf } = η L2 I Voltage Limited 2 Vsup ply 43 Reduction of Design Variables MOSFETs Set Ln and Lp to the process minimum to reduce parasitic capacitances and maximize gm Constrain gm,n=gm,p to maintain symmetry and reduce 1/f noise (this constrains Wn and Wp) This leaves only one independent variable Wn now called just W Cload Set by input capacitance of output drive amplifier Choose to drive 50 Ohm load with minimum voltage swing The specifies an output differential pair with a specific W/L and hence a specific Cload VDD Vtune Cload L C gres Cload -g Vbias 44 Area Constrained Inductor Design Inductor Reduced inductor area always leads to higher inductor resistance so choose D=Dmax So the independent design variables are w, s, and n w D S Lower L and Lower Rs 45 Design Constraints in the C-w Plane Start up g ≥ α min g res 1 ≤ ωmax LCmin Cv,max Voltage Swing Region for feasible designs Current Limited 1 ≥ ωmin LCmax Voltage Limited w 46 Contours of Constant Phase noise Start up g ≥ α min g res 1 ≤ ωmax LCmin Voltage Swing Region for feasible designs Cv,max Optimum Design Current Limited For this inductor Voltage Limited 1 ≥ ωmin LCmax L{Δf } = constant w L{Δf } = 2 η L2 g res I Current Limited 47 Effect of inductor gL What happens if we keep the same inductance but change the geometrical design parameters so that we have higher loss? Start up g ≥ α min g res 1 ≥ ωmin LCmax Voltage Swing Cv,max Vsw,max I = g res 1 ≤ ωmax LCmin Current Limited Voltage Limited Voltage Swing w Conclusion: Minimum phase noise for a given inductance occurs for the inductor design that has the minimum gL Low gL High gL 48 What happens as we change the inductor? L{Δf } = η L2 I 2 Vsup ply L{Δf } = RL gL w 2 η L2 g res Current Limited I ( D ) RP = RS Q 2 + 1 ≅ RS Q 2 Rp = gL = Inductance Minimum gL as a function of L for spiral inductor designs Voltage Limited (ω0 LS ) 2 S RS RS (ω0 LS ) g res = L 2 C gres -g 1 ( go,n + go , p + gv + g L ) 2 For minimum phase noise use the smallest inductor that you can and still meet the design constraints. 49 Design Constraints in the C-w Plane Start up g ≥ α min g res 1 ≤ ωmax LCmin Cv,max Voltage Swing Region for feasible designs Current Limited 1 ≥ ωmin LCmax Voltage Limited w 50 Optimization Process VDD 1) Set bias current to Imax 2) Choose an Inductor value and then choose and inductor design that minimizes gL 3) Draw design constraints in the c-w plane 4) If a feasible design point exists decrease inductance and repeat 5) Continue until the feasible design area shrinks to a point in the c-w plane or either the tuning, swing or stat up conditions cannot be satisfied Vtune Cload Cload Vbias w D S 51 Bonus Material • Rotary Traveling Wave Oscillators – A low power, high frequency, low phase noise oscillator with and “infinite” number of available phases. 52 Genesis of the RTWO VDD VDD 53 Rotary Wave Genesis Wave + + - - 0 0 Z 0 0 0 0 vp 0 0 L per_m Cper_m 1 L per_m. Cper_m 0 0 0 0 Transmission line NOT LC tuned circuit characteristic. 54 Möbius “Termination” - Null 0 Tail [ + L total. Ctotal ]. 2 - + 0 + - Supports a Square Wave. 1 fosc Wave + + 2 laps required - + Transmission line NOT LC tuned circuit characteristic. 55 Rotary Clock Visualization 1 L . C per_m 1 L total. Ctotal .2 Philip Restle, IBM per_m fosc 56 Distributed Amplifier The design of the distributed amplifiers was first formulated by William S. Percival in 1936 Percival proposed a design by which the transconductances of individual vacuum tubes could be added linearly, thus arriving at a circuit that achieved a gain-bandwidth product greater than that of an individual tube. Not well known until a publication on the subject was authored by Ginzton, Hewlett, Jasberg, and Noe in 1948 57 An alternative derivation: Modern Integrated Distributed Amplifier 58 A Differential Distributed Amplifier Transmission lines 59 A Differential Distributed Oscillator Which can be "unwound" into this: 60 Analytic Formulation of RTWO PDE Modeled as continuous conductance G(V) per length … … Transmission line with L, C, R per length Nonlinear PDE describing differential mode on Transmission line ∂V 2 ∂V 2 ∂V − LC 2 − ( RC + LG ' (V ) ) − RG (V ) = 0 2 ∂z ∂t ∂t Imposition of periodic boundary conditions on F: F(x)=F(x+2l0) Defines RTWO Solutions, where lo is Consider G (V ) = - g1V + g3V 3 simplist "Van der Pol" like driving term. the transmission line 1 ⎞ " ⎛ 2 ' 3 length ⎜ LC − 2 ⎟ F + ( RC − Lg1 + 3Lg3 F ) F − Rg1 F + Rg3 F = 0 Consider steady traveling wave solutions of the type: z ⎛ z⎞ F ⎜ t- ⎟ substitute to get an ODE in x ≡ tv ⎝ v⎠ 1 ⎞ " ⎛ ' ' ⎜ LC − 2 ⎟ F + ( RC + LG ( F ) ) F + RG ( F ) = 0 V ⎠ ⎝ ⎝ V ⎠ "Mass" Loss and saturable gain Van der Pol-Duffing Equation Nonlinear "soft" spring Perturbation solutions possible using Jacobi-Elliptic Functions as basis 61 Approximate Solution Using Harmonic Balance ⎡⎛ ⎤ ⎛ε ⎞ 1 ⎞ ⎛ 1 ⎞ ⎛ 3 ⎞ F ( x, ε ) = ⎢⎜ 2 + ε 2 ⎟ ⋅ cos kω x + ⎜ − ε ⎟ ⋅ sin ( 3kω x ) + ⎜ − ε 2 ⎟ ⋅ cos ( 3kω x ) ⎥ × ⎜ ⎟ 64 ⎠ ⎝ 4 ⎠ ⎝ 32 ⎠ ⎣⎝ ⎦ ⎝η ⎠ Where η= −3Lg3 1 v 2 − LC Rg1 ε= ( RC − Lg1 ) × 1 v 2 − LC 2 Rg1 k= Rg1 1 1 v 2 − LC Oscillation Condition Lg1 − RC > 0 Simplified results for reasonable component values Effective Velocity of wave V= 1 LC 2 1 2 1 ⎧ ⎫ ⎪ ⎛ 1 ⎞ 2 ⎡⎛ ω0 L ⎞ 3 ⎛ g1 ⎞ ⎛ ω0 L ⎞ 3 ⎛ g1 ⎞ ⎤ ⎪ ⎢ 1 + ⋅ ⋅ + ⋅⎜ ⎨ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟⎥ ⎬ ⎜ ⎟ ⎟ ⎝ 32 ⎠ ⎢⎣⎝ R ⎠ ⎝ ω0C ⎠ ⎝ R ⎠ ⎝ ω0C ⎠ ⎥⎦ ⎪ ⎩⎪ ⎭ Oscillator Frequency −1 1/ 2 2 1 LC ≈ Velocity of unloaded lossless line 2 4 2 ⎡ 2 3 3 3 1 2 2 2 4 ⎢ l0 3 ⋅ g1 ⋅ R − 3 ⋅ ⎛⎜ L ⎞⎟ ± l0 3 ⋅ g12 ⋅ R − 3 ⋅ ⎛⎜ L ⎞⎟ + 4 ⋅ ( 32 ) 3 ⋅ R 3 ⋅ ⎛⎜ L ⎞⎟ ⎢ 1 ⎝C⎠ ⎝C⎠ ⎝C⎠ ω= ×⎢ 2 l0 LC ⎢ ⎢ Frequency of Fundamental mode of Mobius ⎣ terminated lossless transmission line Results verified against exact simulation ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ 3 ⎡ ⎛ lo ⎞2 ⎤ ⎢1 − ⎜ ⎟ Rg1 ⎥ π ⎝ ⎠ ⎥⎦ ⎣⎢ Correction terms due to line loss and gain 2 1/ 2 ≈ 2 ⎤ 2π ⎡ ⎛ lo ⎞ ⎢1 − ⎜ ⎟ Rg1 ⎥ 2lo LC ⎣⎢ ⎝ π ⎠ ⎥⎦ 62 Number of allowed modes f osc A For an RTWO of length L equal to NA the oscillation frequency will be v v = p or integer multiples of this frequency f osc = n p 2N A 2NA 1 = 2 N ( L + Lm )(2Cm + C ) N=5 using vp = A ( L + Lm )(2Cm + C ) Recall cutoff frequency, above this frequency propagation ceases fc = 1 π ( L + Lm )( 2Cm + C ) so for a lumped or periodically loaded realization modes can exist up to f osc < f c which implies For a realization that yields a given fundamental frequency more possible modes n can exist if the stages are more finely divided (Greater N) L that the number of allowed modes n is n= C Lm L 2N π Cm C 63 Implication of Finite Number of Modes f ( x) = 2 ∑ π n m =1 1 sin((2m + 1) x) 2m + 1 n=1 (2x) n=4 (9x) n=0 2 f '( x) = ∑ π f '(0) = 2n π n m =1 cos((2m + 1) x) Oscillator risetime increases with the number of allowed modes which depends on the number of stages used in the oscillator design. 64 Phase Noise Characteristics For RTWO Z0=T-line impedance, it2/Δf Thermal noise, N=Number of sections, QL=Q of loaded T-line, ω0=oscillator frequency, Δω=frequency offset G. Le Grand de Mercey PhD. Thesis 65 Bandwidth Rise Time • Distributed structure leads to very high bandwidth – – – – – – Parasitic capacitance absorbed into transmission lines impedance Gates and drains driven by differential signal Transistor doesn’t need to drive drain capacitance Similarly the gate capacitance is part of the transmission line Load capacitance also becomes transmission line impedance Switching speed determined by the gate resistance Rg and Cgs. • Rise/fall time can be controlled by segment number – Cutoff frequency: f cutoff = 1 2π ⋅ Llump ⋅ Clump – Rise/fall time depends on the cutoff frequency – Practically the limit is the capacitive load 66 Inverter Sizing As with a more standard differential L-C oscillator sufficient gain must be supplied to overcome the line losses, this leads to a condition on the total transconductance due to all the inverters necessary for startup and sustained oscillations. Gm > 1 1 2 Z 0 1 − α nl / 2 + α 2 n 2l 2 / 6 Where Z 0 = Loaded line impedance α = transmission line attenuation coefficient n = number of stages l = length of each section 67 Low Power Design Considerations Pdiss 2 Vodd = 2 R Z odd Z odd = ( L + Lm ) 2Cm + C μ ⎛⎛ πs ⎞ ⎞ L + Lm ≈ o log ⎜ ⎜ ⎟ + 1⎟ π ⎝ ⎝ w+t ⎠ ⎠ •For low power operation the resistive losses in the transmission line must be mimimized and the circulating current must be reduced by using a high transmission line impedance •ZO is maximized by increasing L this implies the use of narrow conductors that are widely separated to construct the differential transmission line •To achieve wide tuning however the necessary varactor loading will increase the power at low frequencies Where s is the line spacing w is the conductor width and t is the metal thickness 68 References Y. Chen, K. Pedrotti “Rotary Traveling Wave Oscillators, Analysis and Simulation” to be published IEEE TCAS-1 A. Hajimiri, T. H. Lee, “A general theory of phase noise in electrical oscillators”, IEEE Journal of Solid State Circuits, vol. 33, no. 2, February 1998 D. Ham, A. Hajimiri, “Design and Optimization of a Low Noise 2.4GHz CMOS VCO with Integrated LC Tank and MOSCAP Tuning”, IEEE International Symposium on circuits and systems, part 1, pp I-331-I-334, 2000 Ali Hajimiri, Thomas H. Lee, "The Design of Low Noise Oscillators" Kluwer Academic Publishers, March 1999 E. Hegazi, J. Rael, A. Abidi, The Designers Guide to High Purity Oscillators, Klewer, 2005 D. B. Leeson, “A Simple model of feedback oscillator noise spectrum”, Proceeding of the IEEE, vol. 54, pp. 290-307, August 1967 G. Le Grand de Mercey “18 GHz-36 GHz Rotary Traveling Wave Voltage Controlled Oscillator in a CMOS Technology” PhD. Thesis Universitat der Bundeswehr Munchen August 2004 69 References Ulrich L. Rohde, Ajay K. Poddar, Georg Böck "The Design of Modern Microwave Oscillators for Wireless Applications ", John Wiley & Sons, New York, NY, May, 2005 C. Toumazou et. Al. eds, Tradeoffs in Analog Circuit Design: The Designers Companion, Klewer, 2002 L. Rawlings, The Science of Clocks and Watches, British Horological Institute, 3rd ed., 1993 E. Vittoz, M. Degrauwe, S. Bitz, “High-Performance Crystal Oscillator Circuits: Theory and Application: IEEE, JSSC, Vol. 20, No. 3, June 1988 C.J. White, and A. Hajimiri “ Phase Noise in Distributed oscillators ”, Electronics Letters 2002, vol. 38, NO. 23 pp. 1453-1454 J. Wood, T.C. Edwards, and S. Lipa, “Rotary Traveling-Wave Oscillator Arrays: A New Clock Technology”, IEEE Journal of Solid-State Circuits, vol. 36 , pp. 1654-1665. 70