Download Chapter 5 Combinatorics (Recap)

Chapter 5 Combinatorics (Recap)
The Sum Rule: Given tasks T1, T2, …, Tk, with task Ti having
exactly ni possible outcomes, the number of ways to perform one
of these k tasks is n1 + n2 + … + nk.
The Product Rule: Given tasks T1, T2, …, Tk, with task Ti having
exactly ni possible outcomes, the number of possible ways to
perform all of these k tasks is n1•n2• …•nk.
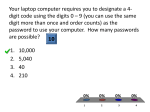
Example: At a local deli you can choose from six kinds of soda,
10 kinds of sandwiches and 12 desserts. How many ways are
there to order:
a. a sandwich
b. exactly one item
c. a full meal (soda, sandwich and dessert)
d. any two items (repetition allowed)
e. any two distinct items
f. items of two different kinds
Permutations (order matters) and Combinations (order doesn’t matter
P(n, r) =
C(n, r) =
The Powerball Lottery
Rules of the Game
Ways to Win
Counting the number of ways to win
The number of possible powerball tickets is:
Variations of the basic problem
More Powerball Examples
Number of orders in which the white balls can be chosen
Number of sets of white balls that can be chosen
Number of sets of white balls that contain 13 or 43 but not both
Number of ways to win a lesser prize
a. Match only the powerball
b. Match exactly three white balls and not the powerball
c. Match exactly three white balls and the powerball
d. All balls chosen contain even numbers
Example—the Pick Three Game
Rules:
Ways to win:
More examples
Example 1: How many five card poker hands contain
a. 2 spades and 3 red cards
b. 2 cards each of two ranks
c. all red cards with two cards each of two ranks
d. exactly one queen and exactly three spades
e. contain at least one ace?
Why won’t the following approach work?
Example 2: How many ternary strings of length 10 are there with
a. exactly two 0’s, three 1’s and five 2’s
b. exactly two 0’s, three 1’s and five 2’s with each 1 immediately
preceded by a 2.
Example 3: You invite nine friends to join you at dinner. How
many ways can the ten of you be seated around a circular table?
Inclusion/Exclusion Examples
Example 1: Let S = {a, b, c, d, e, f}. How many strings of length 5
begin or end with a?
Example 2: Find the number of positive integers  100 that are
even or divisible by 7.
Example 3: Find the number of four digit numbers that have
exactly one 3.
Case 1:
Case 2:
More Examples
Example 4: Let S = {1, 2, …, 10}. The number of subsets of S that
a. contain exactly 4 odd numbers is
b. contain exactly 6 elements, exactly two of which are even is
c. contain 2 but not 5 is
Example 5: Find the number of bit strings of length 10 that
contain 5 consecutive 0’s or 5 consecutive 1’s.
Example 6: How many strings of length 6 can be made from the
letters in the set {a, b, c, d, e, f} which contain exactly one c or
exactly one d.
Example 7: A fly travels along a 44 grid moving from the lower
left to the upper right corner. If no diagonal moves are allowed,
how many paths are there which could be taken?
Binomial Theorem
(a + b)0 = 1
(a + b)1 = a + b
(a + b)2 =
(a + b)3 =
The binomial theorem:
(a + b)n = C(n, 0)an + C(n, 1)an-1b + C(n, 2) an-2b2 + …
+ C(n, n-1)abn-1 + C(n, n)bn
Pascal’s Identity: C(n, k) = C(n-1, k) + C(n-1, k-1).
Algebraic proof of the identity:
C(n-1, k-1) = _____(n-1)!___ = ___(n-1)!__ and C(n-1, k) = __(n-1)!__
(k-1)! (n-1-(k-1))! (k-1)! (n-k)!
k! (n-k-1)!
Combinatorial Proof of the identity
There are two ways to get a subset of S of size k
1:
2:
More on Binomial Coefficients
Example: find the coefficient of x5y4 in the expansion of (x + y)9
Find the coefficient of x9 in the expansion of (2 - x)19.
Show C(n+1, k) = (n+1)•C(n, k-1)/k
Generalized Permutations and Combinations
How many arrangements are there of the letters in the word
TOPEKA?
How many arrangements are there of the letters in the word
Kansas?
Combinations with Repeated Elements
A publisher has 3000 copies of a book to be distributed to three
warehouses. How many ways are there to do this?
Four friends each buy one pair of shoes from a selection of 14
different kinds. How many ways are there to choose the shoes?
Counting Methods to try
To count the number of …
Subsets of n-element set
e.g. number of distinct subsets
from the letters in {a, b, c, d, e}
Outcomes of successive events
e.g. number of ways to award 1st,
2nd and 3rd prizes
Outcomes of disjoint events
e.g. ways to pick either a dog or a
cat from a pet store
Outcomes given specific choices at
each step
e.g. number of ways a best 3 of 5
series can be played
Elements in nondisjoint sets
e.g. pick a spade or a queen from a
deck of cards
Ordered arrangements of r objects out
of n distinct objects
e.g. number of 5 letter words from
{a,…z} without repetition
Ordered arrangements of r objects out
of n distinct objects, repetition allowed
e.g. strings of length 6 from the
set {a,b,c,d}
Ways to choose r out of n distinct
objects
e.g. committee of size five from a
group of size 20
Ways to choose r out of n distinct
objects with repetition allowed
e.g. choose 6 pieces of fruit from
baskets of apples and pears
Method to try
Use formula 2n
Multiply number of outcomes for
each event
Add number of outcomes for each
event
Use a decision tree
Use inclusion exclusion
Use P(n, r) formula
Use nr formula
Use C(n, r) formula
Use C(r + n - 1, r) formula
Modification of Table 3.2 in Gersting
Decision trees