* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Descriptive Statistics
Psychometrics wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
Foundations of statistics wikipedia , lookup
Resampling (statistics) wikipedia , lookup
Statistical inference wikipedia , lookup
Time series wikipedia , lookup
History of statistics wikipedia , lookup
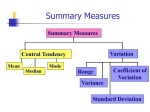
Descriptive & Inferential Statistics Adopted from ;Merryellen Towey Schulz, Ph.D. College of Saint Mary EDU 496 The Meaning of Statistics Several Meanings • Collections of numerical data • Summary measures calculated from a collection of data • Activity of using and interpreting a collection of numerical data • Last year’s enrollment figures • Average enrollment per month last year • Evaluators made a projection of next year’s enrollments Descriptive Statistics • Use of numerical information to summarize, simplify, and present data. • Organized and summarized for clear presentation • For ease of communications • Data may come from studies of populations or samples Descriptive Statistics Associated with Methods and Designs Design Descriptive Statistics Survey Studies Percentages, measures of central tendency and variation Meta-analysis Effect sizes Causal comparative studies Measures of central tendency & variation, percentages, standard scores Experimental Measures of central tendency & variation, percentages, standard scores, effect sizes Descriptive Stats Vocabulary • • • • • • • • Central tendency Mode Median Mean Variation Range Standard deviation Normal distribution Descriptive Stats Vocabulary cont’d • • • • Standard score Effect size Correlation Regression Inferential Statistics • To generalize or predict how a large group will behave based upon information taken from a part of the group is called and INFERENCE • Techniques which tell us how much confidence we can have when we GENERALIZE from a sample to a population Inferential Stats Vocabulary • • • • • • • Hypothesis Null hypothesis Alternative hypothesis ANOVA Level of significance Type I error Type II error Examples of Descriptive and Inferential Statistics Descriptive Statistics Inferential Statistics • Graphical – Arrange data in tables – Bar graphs and pie charts • Numerical – Percentages – Averages – Range • Relationships – Correlation coefficient – Regression analysis • Confidence interval • Margin of error • Compare means of two samples – Pre/post scores – t Test • Compare means from three samples – Pre/post and follow-up – ANOVA = analysis of variance Problems With Samples • Sampling Error – Inherent variation between sample and population – Source is “chance or luck” – Results in bias • Sample statistic -- a number or figure – Single measure -- how sure accurate – Comparing measures --see differences • How much due to chance? • How much due to intervention? What Is Meant By A Meaningful Statistic (Significant)? • Statistics, descriptive or inferential are NOT a substitute for good judgment – Decide what level or value of a statistic is meaningful – State judgment before gathering and analyzing data • Examples: – Score on performance test of 80% is passing – Pre/post rules instruction reduces incidents by 50% Interpretation of Meaning • Population Measure (statistic) – There is no sampling error – The number you have is “real” – Judge against pre-set standard • Inferential Measure (statistic) – Tells you how sure (confident) you can be the number you have is real – Judge against pre-set standard and state how certain the measure is Descriptive Statistics for one variable Statistics has two major chapters: • Descriptive Statistics • Inferential statistics Statistics Descriptive Statistics • Gives numerical and graphic procedures to summarize a collection of data in a clear and understandable way Inferential Statistics • Provides procedures to draw inferences about a population from a sample Descriptive Measures • Central Tendency measures. They are computed to give a “center” around which the measurements in the data are distributed. • Variation or Variability measures. They describe “data spread” or how far away the measurements are from the center. • Relative Standing measures. They describe the relative position of specific measurements in the data. Measures of Central Tendency • Mean: Sum of all measurements divided by the number of measurements. • Median: A number such that at most half of the measurements are below it and at most half of the measurements are above it. • Mode: The most frequent measurement in the data. Example of Mean Measurements x Deviation x - mean 3 -1 5 1 5 1 1 -3 7 3 2 -2 6 2 7 3 0 -4 4 0 40 0 • MEAN = 40/10 = 4 • Notice that the sum of the “deviations” is 0. • Notice that every single observation intervenes in the computation of the mean. Example of Median Measurements Measurements Ranked x x 3 0 5 1 5 2 1 3 7 4 2 5 6 5 7 6 0 7 4 7 40 40 • Median: (4+5)/2 = 4.5 • Notice that only the two central values are used in the computation. • The median is not sensible to extreme values Example of Mode Measurements x 3 5 5 1 7 2 6 7 0 4 • In this case the data have tow modes: • 5 and 7 • Both measurements are repeated twice Example of Mode Measurements x 3 5 1 1 4 7 3 8 3 • Mode: 3 • Notice that it is possible for a data not to have any mode. Variance (for a sample) • Steps: – Compute each deviation – Square each deviation – Sum all the squares – Divide by the data size (sample size) minus one: n-1 Example of Variance Measurements Deviations x 3 5 5 1 7 2 6 7 0 4 40 x - mean -1 1 1 -3 3 -2 2 3 -4 0 0 Square of deviations 1 1 1 9 9 4 4 9 16 0 54 • Variance = 54/9 = 6 • It is a measure of “spread”. • Notice that the larger the deviations (positive or negative) the larger the variance The standard deviation • It is defines as the square root of the variance • In the previous example • Variance = 6 • Standard deviation = Square root of the variance = Square root of 6 = 2.45 Percentiles • The p-the percentile is a number such that at most p% of the measurements are below it and at most 100 – p percent of the data are above it. • Example, if in a certain data the 85th percentile is 340 means that 15% of the measurements in the data are above 340. It also means that 85% of the measurements are below 340 • Notice that the median is the 50th percentile For any data • At least 75% of the measurements differ from the mean less than twice the standard deviation. • At least 89% of the measurements differ from the mean less than three times the standard deviation. Note: This is a general property and it is called Tchebichev’s Rule: At least 1-1/k2 of the observation falls within k standard deviations from the mean. It is true for every dataset. Example of Tchebichev’s Rule Suppose that for a certain data is : • Mean = 20 • Standard deviation =3 Then: • A least 75% of the measurements are between 14 and 26 • At least 89% of the measurements are between 11 and 29 Further Notes • When the Mean is greater than the Median the data distribution is skewed to the Right. • When the Median is greater than the Mean the data distribution is skewed to the Left. • When Mean and Median are very close to each other the data distribution is approximately symmetric.