Download Descriptive Statistics

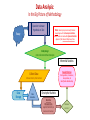
INTRO TO RESEARCH METHODS
SPH-X590 SUMMER 2015
DATA ANALYSIS: METHODOLOGICAL BIG
PICTURE
STATISTICAL ANALYSIS
PROBABILITY, INFERENCE & ESTIMATION
NOTATION
Presentation Outline
• Review
o
o
o
o
Structure of Research
Dimensions of Research
Research Process
Study Designs
• Statistical Analysis
o Types of Statistics: Descriptive and Inferential
o Notation
The Structure of Research:
Deduction
The “Hourglass" Notion of Research
Begin with broad questions narrow down, focus in.
Operationalize
OBSERVE
Analyze Data
Reach Conclusions
Generalize back to Questions
The Scientific Method
Problem/Question
Observation/Research
Formulate a Hypothesis
Experiment
Collect and Analyze Results
Conclusion
Communicate the Results
The Empirical Research Process:
Step 1 Identification of Area of Study: Problem Formulation
D
E
D
U
C
T
I
O
N
T
H
E
O
R
Y
Step 2 Literature Review: Context
Step 3 Research Objectives to Hypotheses: Content to Methodology
•
Concepts to Variables
Step 4 Study Design I: Data Collection Methods
•
•
Research Design: experimental, quasi-experimental, or non-experimental
Time & Unit of Analysis
Step 5 Procedures: Sampling, Assignment, Recruitment, & Ethics
Step 6 Collection: Instruments, Materials, & Management
Step 7 Study Design II: Analysis
•
•
Statistical Approaches & Analytical Techniques
Sample Size & Power
Step 8 Results: Dissemination
•
Publication, Presentation, & New Application
The Dimensions of Empirical Research:
A movement from the theoretical to analytical
Theories
Analysis
Data Collection
Hypotheses
Deductive
Reasoning
EMPIRICAL
RESEARCH
SCIENTIFIC METHOD
Variables
Constructs
Propositions
Concepts
Measurement
Postulates
Data Analysis:
In the Big Picture of Methodology
Question to Answer
Hypothesis to Test
Theory
Note: Results of empirical scientific studies
always begin with the Descriptive Statistics,
whether results conclude with Inferential Statistics
depends of the Research Objectives/ Aims
Study Design:
Data Collection Method & Analysis
Inferential Statistics
Causal Inference
Collect Data:
Test Hypothesis, Conclusions,
Interpretation, &
Identification Relationships
Measurements, Observations
Data
Storage
Data
Extraction
Descriptive Statistics
Describe
Characteristics
Organize, Summarize, &
Condense the Numbers
Decision:
Statistics?
Data Analysis:
Types of Statistics
•
Descriptive Statistics
o Summarization & Organization of variable values/scores
for the sample
•
Inferential Statistics
o Inferences made from the Sample Statistic to the
Population Parameter.
o Able to Estimate Causation or make Causal Inference
• Isolate the effect of the Experimental (Independent) Variable
on the Outcome (Dependent) Variable
Data Analysis:
Descriptive Statistics
• Descriptive Statistics are procedures used for organizing and summarizing
scores in a sample so that the researchers can describe or communicate the
variables of interest.
• Note: Descriptive Statistics apply only to the sample: says nothing about how
accurately the data may reflect the reality in the population
• Use Sample Statistics to “infer” something about relationships in the entire
population: assumes sample is representative of population.
• Descriptive Statistics summarize 1 variable: aka Univariate Statistics
• Mean, Median, Mode, Range, Frequency Distribution, Variance and
Standard Deviation are the Descriptive Statistics: Univariates
Data Analysis:
Inferential Statistics
• Inferential Statistics are procedures designed to test the likelihood of finding the same
results from one sample with another sample drawn from the same population: in
fact, mathematically tests whether the sample results would be obtained if all possible
samples from the population were tested.
• Attempts to rule out chance as an explanation for the results: that results reflect real
relationships that exist in the population and are not just random or only by chance.
• Before you can describe or evaluate a relationship using statistics, you must design
your study so that your research question can be addressed.
• This is Methodology: where theory meets Data Collection
Methods & Data Analysis.
Data Analysis:
Statistics Notation
Capitalization
In general, capital letters refer to
population attributes (i.e., parameters);
and lower-case letters refer to sample
attributes (i.e., statistics).
For example,
• P refers to a population proportion;
o and p, to a sample proportion.
• X refers to a set of population
elements;
o and x, to a set of sample
elements.
• N refers to population size;
o and n, to sample size.
Greek vs. Roman Letters
• Like capital letters, Greek letters refer to
population attributes.
• Their sample counterparts, however, are
usually Roman letters.
For example,
• μ refers to a population mean;
o and x, to a sample mean.
• σ refers to the standard deviation of a
population;
o and s, to the standard deviation of
a sample.
Data Analysis:
Statistics Notation
Population Parameters
By convention, specific symbols represent
certain population parameters.
Notation
• μ refers to a population mean.
• σ refers to the standard deviation of a
population.
• σ2 refers to the variance of a population.
• P refers to the proportion of population
elements that have a particular attribute.
• Q refers to the proportion of population
elements that do not have a particular
attribute, so Q = 1 - P.
• ρ is the population correlation coefficient,
based on all of the elements from a
population.
• N is the number of elements in a
population.
Sample Statistics
By convention, specific symbols represent
certain sample statistics.
Notation
• x refers to a sample mean.
• s refers to the standard deviation of a
sample.
• s2 refers to the variance of a sample.
• p refers to the proportion of sample
elements that have a particular attribute.
• q refers to the proportion of sample
elements that do not have a particular
attribute, so q = 1 - p.
• r is the sample correlation coefficient,
based on all of the elements from a sample.
• n is the number of elements in a sample.
Data Analysis:
Summation/ Sigma Notation
Summation Notation is shorthand that relies on Greek alphabet and mathematical
symbols to indicate how to process values: aka formulae.
•  = summation
• X = Variable
What do each of these mean?
• X
o Add up the values of X
• X + 2 versus (X + 2)
o Add up the values of X and add 2 to the Sum,
o Add 2 to each value of X and then Sum the values
• X2 versus (X)2
o Square each value of X and then Sum
o Sum the values of X and then Square the Sum
• (X + 2)2 versus (X2 + 2)
o Add 2 to each value of X, square the value, then Sum the squared values
o Square each value of X, add 2 to the value, then Sum the values
Data Analysis:
Summation/ Sigma Notation
 : summation
X : Independent Variable, typically
Y: Dependent Variable, typically
N= Size of the Population
n= Size of the Sample
≤ ≥ ≠ = : Equalities or Inequalities
± × ÷ + - : Mathematical Operators
α: alpha, refers to constant/ intercept
µ: mu, sample mean
β: beta coefficient/ standardized
δ: sigma, sample standard deviation
δ2: sigma squared, sample variance