* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Class notes on controlled rectifiers
Electrification wikipedia , lookup
Electric power system wikipedia , lookup
Power over Ethernet wikipedia , lookup
Electrical substation wikipedia , lookup
Control system wikipedia , lookup
Three-phase electric power wikipedia , lookup
Power factor wikipedia , lookup
Audio power wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Stray voltage wikipedia , lookup
History of electric power transmission wikipedia , lookup
Current source wikipedia , lookup
Power engineering wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Surge protector wikipedia , lookup
Two-port network wikipedia , lookup
Schmitt trigger wikipedia , lookup
Voltage regulator wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Voltage optimisation wikipedia , lookup
Power MOSFET wikipedia , lookup
Power inverter wikipedia , lookup
Mains electricity wikipedia , lookup
Alternating current wikipedia , lookup
Buck converter wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Mercury-arc valve wikipedia , lookup
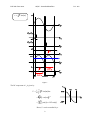
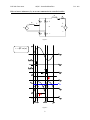
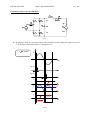
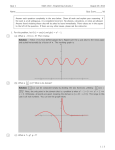
ELEC 431 Class notes AC/DC ‐ Controlled Rectifiers P.K. Jain Controlled rectifier Unlike the uncontrolled rectifiers, by replacing the diodes with thyristors, the average output voltage can be controlled by adjusting the turn-on time or the control angle, denoted by α, of the thyristors (Q1, Q2, Q3 and Q4): The turn-on instant of the thyristor is controlled by the gate signal applied to the thyristor Figure 1 One example is to use the controlled rectifier to control the terminal voltage (vo) in DC machines with armature resistance Ra and inductance La DC machine Figure 2 1 ELEC 431 Class notes AC/DC ‐ Controlled Rectifiers v s = 2V sin (ωt ) Figure 3 The DC component of vo is given by: Vo = 1 π = = π +α ∫ 2V sin (ωt )dωt α 2V π [− cos(ωt )] απ +α 2 2V π cos(α ) ≈ 0.9V cos(α ) Hence, Vo can be controlled by α. 2 P.K. Jain ELEC 431 Class notes AC/DC ‐ Controlled Rectifiers P.K. Jain DC power at the terminal of the rectifier: Pt = Vo I o DC voltage across La = 0 Vo = Ra I o + Eo Eo = Vo − Ra I o Hence, = 0.9V cos(α ) − Ra I o Po = Eo I o Output power of the DC machine: Now, take a look on the input current again: Figure 4 Recall from Fourier series, the fundamental input current of is is given as: is1 = The RMS value of is1 is then: I s1 = 4I o π 4I o 2π sin (ω t − α ) = 2 2I o π ≈ 0.9 I o The total harmonic distortion (THD) in the input current can be calculated to be: = Recall: input power factor is: I s2 − I s21 I s1 = I o2 − 0.81I o2 0.9 I o active or real power Pin = = apparent power S = Vo I o 0.9V cos(α )I o = Vs I s VI o = 0.9 cos(α ) 3 ≈ 0.48 I o Assume lossless, so Pt = Pin ELEC 431 Class notes AC/DC ‐ Controlled Rectifiers When α < π/2 → Po = Vo I o Power flows from AC to DC (rectifying mode/motoring mode) When α > π/2 → Po = −Vo I o Power flows from DC to AC (inverting mode/generating mode) 4 P.K. Jain ELEC 431 Class notes AC/DC ‐ Controlled Rectifiers P.K. Jain Effect of source inductance (Ls) on current commutation in controlled rectifier La Ls Q1 Q2 is vo vs +_ Q4 Q3 Figure 5 v s = 2V sin (ωt ) Figure 6 5 + _ Ra ia + Eo _ ELEC 431 Class notes AC/DC ‐ Controlled Rectifiers P.K. Jain Average output voltage: Vo = 1 π +α ∫ vo dωt = π α +μ 2V = π +α π α ∫+ μ 2V sin (ωt )dωt [− cos(ωt )] απ ++αμ π 2V Vo = Hence, 1 π [cosα + cos(α + μ )] ------------------ (1) Using similar approach in the uncontrolled rectifier case, voltage across Ls is equal to vs for α ≤ ωt ≤ α+µ Ls di Ls = 2V sin (ωt ) dt ωt 2V sin (ωt )d (ωt ) iLs = ωLs α∫ Hence, = At ωt = α, is = -Io which means k = -Io → is = Hence, At ωt = α+µ, → 2V [− cos(ωt ) + cosα ] + k ωLs 2V [− cos(ωt ) + cosα ] − I o ωLs i s = Io Io = 2 I o ωL s 2V 2V [− cos(α + μ ) + cosα ] − I o ωLs = cos α − cos(α + μ ) ------------------------- (2) Substitute (2) into (1) Vo = 2 I ωL ⎞ 2V ⎛ ⎜ cosα + cosα − o s ⎟ π ⎝ 2V ⎠ = 2 2V π 6 cos α − 2 I oωLs π ELEC 431 Class notes AC/DC ‐ Controlled Rectifiers P.K. Jain Controlled rectifier with a parallel diode Figure 7 By placing a diode (DF) across the output of the controlled rectifier, during the negative cycles of vo, DF becomes forward biased and vo is clamped to zero v s = 2V sin (ωt ) vs ωt ig1 ig3 α ωt ig2 ig4 α ωt io Io ωt vo Vo ωt is Io Q2 Q4 turn on 0 α Q1 Q3 turn on ωt π π+α Figure 8 7 2π ELEC 431 Class notes AC/DC ‐ Controlled Rectifiers P.K. Jain Average output voltage: Vo = 1 π ∫ vo dωt = πα 2V = π Power factor = Recall: 2V π π α∫ → When α = π Po = Vo I o = π → Vo = 0 (1 + cosα )I o = Pin 1 Is = 2π = Io 2V power factor = Vo = 2 2V / π Assume lossless thyristors P Pin = S VI s RMS input current: Hence, 2V sin (ωt )dωt (1 + cosα ) When α = 0 Since 1 π (1 + cosα )I o VI o (π − α ) 2π π I o2 ∫0 i dt = 2π 2α∫ dt 2 s (π − α ) π = 2 (1 + cos α ) π (π − α ) π Alternative circuit configuration: Figure 9 By replacing a pair of the thyristors with a pair of diodes (D1 and D2) across the output of the controlled rectifier, vo is clamped during the negative cycles 8