* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download DE C - MSU College of Engineering
Quantum dot wikipedia , lookup
Quantum fiction wikipedia , lookup
Wave–particle duality wikipedia , lookup
Atomic orbital wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
Quantum computing wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Renormalization wikipedia , lookup
Quantum teleportation wikipedia , lookup
Electron configuration wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Quantum machine learning wikipedia , lookup
Quantum group wikipedia , lookup
Particle in a box wikipedia , lookup
EPR paradox wikipedia , lookup
History of quantum field theory wikipedia , lookup
Quantum key distribution wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Quantum state wikipedia , lookup
Hidden variable theory wikipedia , lookup
Canonical quantization wikipedia , lookup
Hydrogen atom wikipedia , lookup
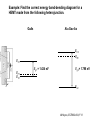
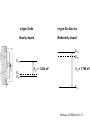
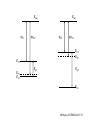
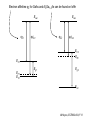
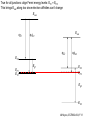
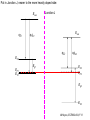
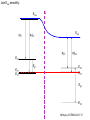
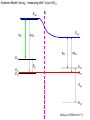
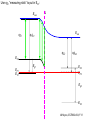
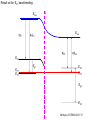
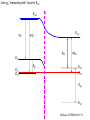
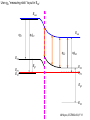
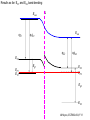
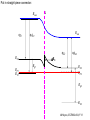
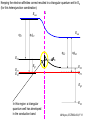
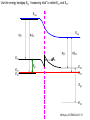
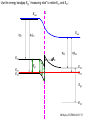
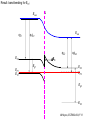
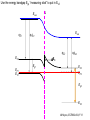
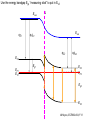
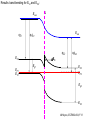
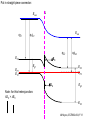
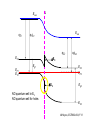
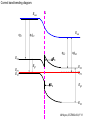
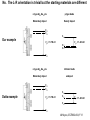
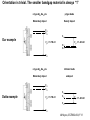
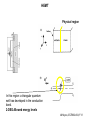
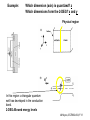
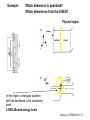
ECE 802-604: Nanoelectronics Prof. Virginia Ayres Electrical & Computer Engineering Michigan State University [email protected] Lecture 02, 03 Sep 13 In Chapter 01 in Datta: Two dimensional electron gas (2-DEG) DEG goes down, mobility goes up Define mobility (and momentum relaxation) One dimensional electron gas (1-DEG) Special Schrödinger eqn (Con E) that accommodates: Confinement to create 1-DEG Useful external B-field Experimental measure for mobility VM Ayres, ECE802-604, F13 Lecture 02, 03 Sep 13 Two dimensional electron gas (2-DEG): Datta example: GaAs-Al0.3Ga0.7As heterostructure HEMT VM Ayres, ECE802-604, F13 MOSFET Sze VM Ayres, ECE802-604, F13 HEMT IOP Science website; Tunnelling- and barrier-injection transit-time mechanisms of terahertz plasma instability in high-electron mobility transistors 2002 Semicond. Sci. Technol. 17 1168 VM Ayres, ECE802-604, F13 For both, the channel is a 2-DEG that is created electronically by band-bending MOSFET 2 x yBp = VM Ayres, ECE802-604, F13 For both, the channel is a 2-DEG that is created electronically by band-bending HEMT VM Ayres, ECE802-604, F13 Example: Find the correct energy band-bending diagram for a HEMT made from the following heterojunction. p-type GaAs n-type Al0.3Ga0.7As Heavily doped Moderately doped EC2 EF2 EC1 EF1 EV1 Eg1 = 1.424 eV Eg2 = 1.798 eV EV2 VM Ayres, ECE802-604, F13 p-type GaAs n-type Al0.3Ga0.7As Heavily doped Moderately doped EC2 EF2 EC1 EF1 EV1 Eg1 = 1.424 eV Eg2 = 1.798 eV EV2 VM Ayres, ECE802-604, F13 Evac qc1 qfm1 qc2 qfm2 EC2 EF2 EC1 EF1 EV1 Evac Eg1 Eg2 EV2 VM Ayres, ECE802-604, F13 Electron affinities qc for GaAs and AlxGa1-xAs can be found on Ioffe Evac qc1 qfm1 qc2 qfm2 EC2 EF2 EC1 EF1 EV1 Evac Eg1 Eg2 EV2 VM Ayres, ECE802-604, F13 True for all junctions: align Fermi energy levels: EF1 = EF2. This brings Evac along too since electron affinities can’t change Evac qc1 Evac qfm1 qc2 qfm2 EC1 EF1 EV1 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Put in Junction J, nearer to the more heavily doped side: Evac qc1 Junction J Evac qfm1 qc2 qfm2 EC1 EF1 EV1 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Join Evac smoothly: Evac qc1 J Evac qfm1 qc2 qfm2 EC1 EF1 EV1 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Anderson Model: Use qc1 “measuring stick” to put in EC1: Evac qc1 J Evac qfm1 qc2 qfm2 EC1 EF1 EV1 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Use qc1 “measuring stick” to put in EC1: Evac qc1 J Evac qfm1 qc2 qfm2 EC1 EF1 EV1 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Result so far: EC1 band-bending: Evac qc1 J Evac qfm1 qc2 qfm2 EC1 EF1 EV1 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Use qc2 “measuring stick” to put in EC2: Evac qc1 J Evac qfm1 qc2 qfm2 EC1 EF1 EV1 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Use qc2 “measuring stick” to put in EC2: Evac qc1 J Evac qfm1 qc2 qfm2 EC1 EF1 EV1 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Results so far: EC1 and EC2 band-bending: Evac qc1 J Evac qfm1 qc2 qfm2 EC1 EF1 EV1 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Put in straight piece connector: Evac qc1 J Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Keeping the electron affinities correct resulted in a triangular quantum well in EC (for this heterojunction combination): J Evac qc1 Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 Eg2 In this region: a triangular quantum well has developed in the conduction band EV2 VM Ayres, ECE802-604, F13 Use the energy bandgap Eg1 “measuring stick” to relate EC1 and EV1: Evac qc1 J Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Use the energy bandgap Eg1 “measuring stick” to relate EC1 and EV1: Evac qc1 J Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Result: band-bending for EV1: Evac qc1 J Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Use the energy bandgap Eg2 “measuring stick” to put in EV2: Evac qc1 J Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Use the energy bandgap Eg2 “measuring stick” to put in EV2: Evac qc1 J Evac qfm1 qc2 qfm2 EC1 EF1 EV1 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Results: band-bending for EV1 and EV2: Evac qc1 J Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 Eg2 EV2 VM Ayres, ECE802-604, F13 Put in straight piece connector: Evac qc1 J Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 DEV Eg2 Note: for this heterojunction: DEC > DEV EV2 VM Ayres, ECE802-604, F13 Put in straight piece connector: Evac qc1 J Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 DEV DEC = D(electron affinities) = qc2 – qc1 (Anderson model) DEV = ( E2 – E1 ) - DEC => DEgap = DEC + DEV Eg2 EV2 VM Ayres, ECE802-604, F13 Put in straight piece connector: Evac qc1 J Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 DEV “The difference in the energy bandgaps is accommodated by amount DEC in the conduction band and amount DEV in the valence band.” Eg2 EV2 VM Ayres, ECE802-604, F13 Evac qc1 J Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 DEV Eg2 NO quantum well in EV NO quantum well for holes EV2 VM Ayres, ECE802-604, F13 Correct band-bending diagram: Evac qc1 J Evac qfm1 qc2 DEC EC1 EF1 EV1 qfm2 Eg1 EC2 EF2 DEV Eg2 EV2 VM Ayres, ECE802-604, F13 Is the Example the same as the example in Datta? HEMT VM Ayres, ECE802-604, F13 No. The L-R orientation is trivial but the starting materials are different n-type Al0.3Ga0.7As p-type GaAs Moderately doped Heavily doped EC2 EF2 Our example Eg2 = 1.798 eV EC1 Eg1 = 1.424 eV EF1 EV1 EV2 n-type Al0.3Ga0.7As intrinsic GaAs Moderately doped undoped EC2 EF2 Datta example Eg2 = 1.798 eV EC1 EF1 Eg1 = 1.424 eV EV1 EV2 VM Ayres, ECE802-604, F13 Orientation is trivial. The smaller bandgap material is always “1” n-type Al0.3Ga0.7As p-type GaAs Moderately doped Heavily doped EC2 EF2 Our example Eg2 = 1.798 eV EC1 Eg1 = 1.424 eV EF1 EV1 EV2 n-type Al0.3Ga0.7As intrinsic GaAs Moderately doped undoped EC2 EF2 Datta example Eg2 = 1.798 eV EC1 EF1 Eg1 = 1.424 eV EV1 EV2 VM Ayres, ECE802-604, F13 HEMT Physical region In this region: a triangular quantum well has developed in the conduction band. 2-DEG Allowed energy levels VM Ayres, ECE802-604, F13 Example: Which dimension (axis) is quantized? z Which dimensions form the 2-DEG? x and y Physical region In this region: a triangular quantum well has developed in the conduction band. 2-DEG Allowed energy levels VM Ayres, ECE802-604, F13 Example: Which dimension is quantized? Which dimensions form the 2-DEG? Physical region In this region: a triangular quantum well has developed in the conduction band. 2-DEG Allowed energy levels VM Ayres, ECE802-604, F13 Example: approximate the real well by a one dimensional triangular well in z ∞ Using information from ECE874 Pierret problem 2.7 (next page), evaluate the quantized part of the energy of an electron that occupies the 1st energy level VM Ayres, ECE802-604, F13 VM Ayres, ECE802-604, F13 U(z) = az z VM Ayres, ECE802-604, F13 n=? m=? a=? VM Ayres, ECE802-604, F13 n = 0 for 1st m = meff for conduction band e- in GaAs. At 300K this is 0.067 m0 a=? VM Ayres, ECE802-604, F13 Your model for a = asymmetry ? ∞ U(z) = 3/2 z U(z) = 1 z z VM Ayres, ECE802-604, F13 D. L. Mathine, G. N. Maracas, D. S. Gerber, R. Droopad, R. J. Graham, and M. R. McCartney. Characterization of an AlGaAs/GaAs asymmetric triangular quantum well grown by a digital alloy approximation. J. Appl. Phys. 75, 4551 (1994) An asymmetric triangular quantum well was grown by molecular‐beam epitaxy using a digital alloy composition grading method. A high‐resolution electron micrograph (HREM), a computational model, and room‐temperature photoluminescence were used to extract the spatial compositional dependence of the quantum well. The HREM micrograph intensity profile was used to determine the shape of the quantum well. A Fourier series method for solving the BenDaniel–Duke Hamiltonian [D. J. BenDaniel and C. B. Duke, Phys. Rev. 152, 683 (1966)] was then used to calculate the bound energy states within the envelope function scheme for the measured well shape. These calculations were compared to the E11h, E11l, and E22l transitions in the room‐temperature photoluminescence and provided a self‐consistent compositional profile for the quantum well. A comparison of energy levels with a linearly graded well is also presented VM Ayres, ECE802-604, F13 Jin Xiao (金晓), Zhang Hong (张红), Zhou Rongxiu (周荣秀) and Jin Zhao (金钊). Interface roughness scattering in an AlGaAs/GaAs triangle quantum well and square quantum well. Journal of Semiconductors Volume 34 072004, 2013 We have theoretically studied the mobility limited by interface roughness scattering on two-dimensional electrons gas (2DEG) at a single heterointerface (triangle-shaped quantum well). Our results indicate that, like the interface roughness scattering in a square quantum well, the roughness scattering at the AlxGa1−xAs/GaAs heterointerface can be characterized by parameters of roughness height Δ and lateral Λ, and in addition by electric field F. A comparison of two mobilities limited by the interface roughness scattering between the present result and a square well in the same condition is given VM Ayres, ECE802-604, F13