* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture-7-Optics
Depth of field wikipedia , lookup
Fourier optics wikipedia , lookup
Anti-reflective coating wikipedia , lookup
Retroreflector wikipedia , lookup
Ray tracing (graphics) wikipedia , lookup
Nonimaging optics wikipedia , lookup
Image stabilization wikipedia , lookup
Schneider Kreuznach wikipedia , lookup
Lens (optics) wikipedia , lookup
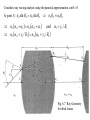
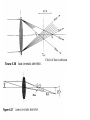
Geometric Optics of thick lenses and Matrix methods Mathematical treatment of refraction for thick lenses shows the existence of principal planes in the paraxial approximation which serve as reference planes for the refraction of rays entering and leaving the system. Symmetry and shape of the lens determine the location of the principal planes. After an analytical treatment1 of refraction for a thick lens geometry: 1 1 nl 1d l 1 nl 1 f R R n R R 2 l 1 2 1 f nl 1d l f nl 1d l and V1 H1 h1 ; V2 H 2 h2 ; h1 ; h2 R2 nl R1nl 1 1 1 (Gaussian form), so si f where Rough approximation for ordinary glass lenses in air: H1H V1V2 / 3 2 1Complete derivation can be found in Morgan, Introduction to Geometrical and Physical Optics. Also, the Newtonian form holds: xo xi f and yo Fig. 6.4 Thick-Lens geometry MT yi x f i yo f xo 2 Note that as dl 0, this will yield the thin lens result. Convention: h1, h2 > 0 then H1, H2 is to the right of V1,V2, and conversely if h1, h2 < 0 then H1, H2 is to the left of V1,V2 Again, H1 and H2 refer to axial points through the principal planes. Now, consider a compound lens consisting of two thick lenses L1 and L2, with the usual parameters so1, si1, f1 and so2, si2 and f2, as shown on the next slide. si, so are image and object distances for the combination si1 si 2 si M T as a whole and are measured s s s o o1 o 2 with respect to H1 and H2. 1 1 1 d fd , H11H1 , and f f1 f 2 f1 f 2 f2 H 22 H 2 fd f1 Note that the sign is important and distances > 0 indicate that H1 or H2 are to the right of H11 or H22. Equivalent thick lens representation of a compound lens Fig. 6.5 A compound thick lens. Note that if the lenses are thin, the pairs of points H11, H12 and H21, H22 coalesce into a single point and d becomes the center to center lens separation. Consider the example of a compound thin lens below (individual lenses are thin). f1 = -30 cm, f2 = 20 cm, d = 10 cm. Then, the effective focal length is 1 1 1 d f f1 f 2 f1 f 2 Since these are thin lenses the H11H1 O1 H1 principal planes converge to single points O1, O2: f 30 cm fd (30)(10) 15 cm f2 20 fd (30)(10) H 22 H 2 O2 H 2 10 cm f1 30 A compound thin lens Analytical Ray Tracing: 3D: 2D: ni kˆi uˆn nt kˆt uˆn ni sin i nt sin t Example of a computer program for ray tracing. Consider a ray tracing analysis using the paraxial approximation, sin At point P1: ni1 sin i1 nt1 sin t1 ni1 i1 1 nt1 t1 1 ni1i1 nt1t1 and 1 y1 / R1 ni1 i1 y1 / R1 nt1 t1 y1 / R1 Fig. 6.7 Ray Geometry for thick lenses n n nt1 t1 ni1 i1 t1 i1 y1 R1 n n Let D1 t1 i1 nt1 t1 ni1 i1 D1 y1 R1 D1 is called the power of a single refracting surface. For a thin lens, D D1 D2 1 nl 1 1 1 f R1 R2 Also, from the geometry y2 y1 d 21 t1 This is done for cosmetic reasons. where d 21 V2V1 nt1 t1 ni1 i1 D1 yi1 Thus, in matrix form we can write: and yt1 0 yi1 y1 nt1 t1 1 D1 ni1 i1 y 0 y 1 i1 t1 Development of Matrix Method Introduce ray vectors 2 1 column matrix: n rt1 t1 t1 and yt1 n ri1 i1 i1 yi1 and a 2 2 refraction matrix: 1 D1 R1 r R r t1 1 i1 1 0 Also ni 2 nt1 , i 2 t1 so ni 2 i 2 nt1 t1 0 and y2 yi 2 d 21 t1 yt1 0 nt1 t1 ni 2 i 2 1 y y d / n 1 i 2 21 t1 t1 Thus, we can define a 2 2 transfer matrix: ray at P2 ray at P1 Thus ri 2 T21rt1 T21 R1ri1 0 1 T21 d / n 1 21 t1 Note : T21 R1 T21 R1 1 Continuing with the second interface in the figure (Fig. 6.7) 1 D2 nt 2 ni 2 with R2 and D2 1 R2 0 so rt 2 R2 T21 R1ri1 Define the system matrix : A R2 T21 R1 rt 2 R2 ri 2 Note A 1 Let d 21 d l and nt1 nl Note that the determinant must be 1 and is a check of the system matrix. After multiplying out the system matrix, its components can be written explicitly: D2 d l D1 D2 d l D1 D2 1 a a nl nl A 11 12 D1d l dl a21 a22 1 n n l l Where d21= dl is the lens thickness and the refractive index of the lens is nt1 = nl. Note that an examination of the system matrix A gives The lens is taken to D1 D2 d l nl 1 1 nl be in air, as a12 D1 D2 , D1 , D2 nl R1 R2 represented by the 1 1 nl 1d l a12 nl 1 R R R R n 2 1 2 l 1 powers D1 and D2. We observe that this is just the reciprocal of the focal length of a thick lens such that –a12=1/f , and the lens power is 1/f . More generally, if the media are different on both sides we would have: ni1 nt 2 ni1 1 a11 nt 2 a22 1 a12 ; Finally , V1 H1 and V2 H 2 fo fi a12 a12 Thus, the matrix method involving 2 2 refraction and transfer matrices enables a determination of fundamental optical system parameters such as the system focal lengths and position of both principal planes relative to the lens vertices. image ray object ray The first operator T10 transfers the reference point from the object (i.e., PO to P1). The next operator A21 then carriers the ray through the lens. A final transfer operator TI2 brings it to the image plane, PI. T = transfer matrix R = refraction matrix A = system matrix Example of a complex lens system analyzed with the Matrix Method: A71 R7 T76 R6 T65 R5 T54 R4 T43 R3 T32 R2 T21 R1 0 0 1 1 0 . 357 0 . 189 ; T32 T21 1 1.6116 1 1 1.6116 1 0 1 1 ; R1 T43 0.081 1.628 1 0 1.6053 1 1 1.6116 1.6053 1 1 1 R2 27.57 ; R3 3.457 0 0 1 1 0.848 0.198 A71 1.338 0.867 Fig. 6.10 A Tessar lens system. The result of the matrix method easily allows for the solution of the basic lens parameters such as the focal length and position of the principal planes relative to the vertices of the outer lenses. f 5.06 V1 H1 0.77 V7 H 2 0.67 As another example, consider a system of thin lenses in which dl 0. Note that the power of a thin lens is D1 + D2 = D. Then 1 D1 D2 1 D 1 1 / f A (thin lens ) 1 1 0 0 1 0 Suppose that two thin lenses are separated by distance d: H2 H1 O1 O2 d Then, the system matrix can be written as 1 1 / f 2 1 0 1 1 / f1 1 d / f 2 A d 1 d 1 0 1 0 1 / f1 d / f1 f 2 1 / f 2 d / f1 1 Remember that ni1 nt 2 a12 ; fo fi ni1 1 a11 nt 2 a22 1 V1 H1 and V2 H 2 a12 a12 Where ni1 = nt2 =1 and V1 = O1 and V2 = O2 for a thin lens Therefore a12 1 1 1 d , f f1 f 2 f12 O1 H1 fd fd , O2 H 2 f2 f1 Note that the locations of the principal planes H1 and H2 strongly depend on d, which can affect on which side of the lenses the planes are located. It is worth noting that a lens system composed of N thin lenses can easily be treated in the same manner for calculating the focal lengths and locations of the principal planes. 1 2 3 ………N A similar analysis can be performed for a mirror in the paraxial approximation. The result is 1 2n / R Mo 0 1 so rr M o ri remembering n i n r with ri , rr y y r i Note that for a plane mirror R and the system matrix for a mirror reduces to 1 0 M| 0 1 2 f R Lens Aberrations: Deviations from the corresponding paraxial approximation Chromatic Aberrations: n() and ray components having different colors have different effective focal lengths Monochromatic Aberrations: Spherical aberration, coma, astigmatism Recall that we used sin (first order theory in the paraxial approx.) Including addition terms in sin - 3/3! leads to the third-order theory which can explain the monochromatic aberrations. Remember that for a single refracting spherical interface in the 1st order approx: n1 n2 n2 n1 D1 so si R If the approximation for the OPL (lo + li) are improved, the 3rd order treatment gives: 2 2 n1 n2 n2 n1 n1 1 1 n2 1 1 2 h so si R 2so so R 2si R si Where h is the distance above the optical axis as shown in the figure. Rays striking the surface at a greater distance (marginal rays) are focused closer to the vertex V than are the paraxial rays and creates spherical aberration. Marginal rays are bent too much and focused in front of paraxial rays. Distance between the intersection of marginal rays and the paraxial focus, Fi, is known as the LSA (longitudinal spherical aberration). Note: SA is positive for convex lens and negative for a concave lens. TSA (transverse SA) is the transverse deviation between the marginal and paraxial rays on a screen placed at Fi. If the screen is moved to the position LC the image blur will have its smallest diameter, known as the “circle of least confusion,” which is the best place to observe the image. Rule of thumb: Incident ray will undergo a minimum deviation when i T. Remember the dispersing prism: i 1T 2T For an object at , the round side of lens facing the object will suffer a minimum amount of SA. Note that a planarconvex lens can be approximated as two prisms. 2T > 1T and the lower prism results in a greater deviation. Fig. 6.16 Spherical Aberration for a planarconvex lens in both orientations. Similarly if the object and image are to be nearly equidistant from the lenses (so = si =2f), an Equi-Convex shaped lens minimizes SA. Marginal rays give smaller image negative coma f 2f Marginal rays give larger image positive coma 2f f Coma (comatic aberration) is associated with the fact that the principle planes are really curved surfaces resulting in a different MT for both marginal and central rays. Since MT = -si/so , the curved nature of the principal surface will result in different effective object and image distances, resulting in different transverse magnifications. The variation in MT also depends on the location of the object which can result in a negative (a) or positive coma (b) and (c), as demonstrated in the left figure. The imaging of a point at S can result in a “comet-like” tail, known as a coma flare and forms a “comatic” circle on the screen (positive coma in this case). This is often considered the worst out of all the aberrations, primarily because of its asymmetric configuration. Astigmatism: The Meridional Plane contains the chief ray which passes through the center of the aperture and the optical axis. The Sagittal Plane contains the chief ray and is perpendicular to the meridional plane. Fermat’s principle shows that planes containing the tilted rays will give a shorter focal length, which depends on the (i) power of the lens and the (ii) angle of inclination. The result is that there is both a meridional focus FT and a sagittal focus FS. Tilted rays have a shorter focal length. Astigmatism: Note that the cross-section of the beam changes from a circle (1) ellipse (2) line (primary image 3) ellipse (4) circle of least confusion (5) ellipse (6) line (secondary image 7) . Focal length difference FS-FT depends on power D of lens and angle of rays. Chromatic Aberrations: Since the index depends on the wavelength then we can expect that the focal length will depend on the wavelength. 1 1 1 nl 1 f R1 R2 f nl nl ( ) Circle of least confusion