Download spp-scatt_01

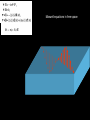
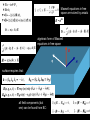
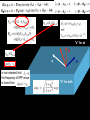
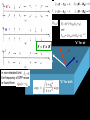
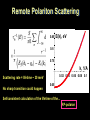
Novel Scattering Mechanisms for
Nanotube-Silicon Devices
Slava V. Rotkin
Surface Polariton in SiO2
Surface phonons in
polar dielectrics:
• due to the dielectric
function difference
between the substrate
and the air, a surface
e.m.w. could exist
Specifics of surface polaritons:
• electric field is not normal to the surface (at 45o)
• electric field decays exponentially from the surface
(not a uniform solution of Maxwell equations)
• dielectric function of
the polar insulator has
a singularity at the
frequency of LO phonon
• surface wave with a
strong decay of the
electric field in the air
appears and interacts
with the NT charges
• existence of a surface mode essentially depends
on existence of the anomalous dispersion region e<0
Maxwell equations in free space
Maxwell equations in free
space are solved by anzatz
E ~ eikz
algebraic form of Maxwell
equations in free space
E
q
surface requires that:
all field components (but
one) can be found from BC:
H
"a" for air
E
q
in non-retarded limit
the frequency of SPP mode
is found from
H
"b" for bulk
E
H
"a" for air
J
E
q
in non-retarded limit
the frequency of SPP mode
is found from
H
"b" for bulk
last component of the field
can be found only with
QM/QED
Charge Scattering:
Short Introduction
Boltzmann Transport Equation (0)
Equilibrium distribution function is
Fermi-Dirac function:
E
e.d.f. is symmetric and thus j = 0
k
asymmetric non-e.d.f. provides: j > 0 (both in ballistic and
diffusive model)
Quantum-mechanical
calculation of the conductivity
may be reduced to the Drude
formula
electron velocity enters the formula
Conductivity: van Hove singularities
Prof. T. Ando
Scattering rate is proportional to
the velocity which diverges at the
subband edge. Thus, the Drude
conductivity has peculiarities at vHs.
Surface Phonon Polariton
Introduction
q
j
Vd
q~area~nm2
channel heating due to Joule losses and low thermal coupling to leads
It exists, however, a relaxation mechanism which transfers the energy
directly to the substrate without intermediate exchange with the SWNT
lattice (phonons) which is an inelastic remote optical phonon scattering
Pioneering work by K. Hess and P. Vogl – back to 1972 – RIP-S in Si.
The mechanism appeared to be ineffective for Si MOS-FETs and was
almost forgotten for decades...
Remote Polariton Scattering
Interaction potential
(e-dipole)
where the (dipole) polarization is calculated following Mahan et al.
here q is the SPP wavenumber; x is normal to the surface
F is related to Froehlich constant:
and wSO is the SPP frequency
Surface Polariton in SiO2
Surface phonons in
polar dielectrics:
• due to the dielectric
function difference
between the substrate
and the air, a surface
e.m.w. could exist
• dielectric function of
the polar insulator has
a singularity at the
frequency of LO phonon
• surface wave with a
strong decay of the
electric field in the air
appears and interacts
with the NT charges
for vF~108 cm/s and wSO~150meV :
e ~ 10
5 V/
cm
Saturation Regime and
Heat Dissipation Problem
Introduction
• Scattering in 1D systems is weak due to restricted phase space
available for the electron: k -> -k.
• However, scattering at high (drift) electric field is inevitable due to
emission of an optical phonon. Which provides a fast relaxation
mechanism for the hot electrons (and holes).
• Inelastic scattering rates have been calculated for SWNTs earlier:
However, recent optics experiments showed faster relaxation rates
for the hot electron, which suggests a new scattering mechanism.
Introduction
Inelastic optical phonon relaxation scattering is likely a factor
determining the saturation current in SWNTs :
The hot electron energy is transferred to the SWNT phonon subsystem.
The energy dissipation depends on the environment (thermal coupling).
Remote Polariton Scattering
T=0K - therefore, only SO-phonon emission is included
Dm=0 - intra-subband transitions
Dm=1 - inter-subband transitions (neglecting higher m's)
q~1/l (forward) and q~2k (backward) scattering
Remote Polariton Scattering
• RPS rate varies for intra-subband and inter-subband scattering
• RPS has maximum at the van Hove singularities (for semiconductor-SWNT)
Conductivity: van Hove singularities
Scattering rate is
proportional to the velocity
which diverges at the
subband edge. Thus, the
Drude conductivity has
peculiarities at vHs.
Prof. T. Ando
Remote Polariton Scattering
• RPS rate varies for intra-subband and inter-subband scattering
• RPS has maximum at the van Hove singularities (for semiconductor-SWNT)
inter-subband transitions are negligible due to
non-zero angular momentum transfer
Remote Polariton Scattering
0.85
E(k), eV
0.8
0.75
k, 1/A
0.02 0.04 0.06 0.08 0.1
Scattering rate = lifetime ~ 30 meV
No sharp transition could happen
0.65
Selfconsistent calculation of the lifetime of the...
RP-polaron
Surface Polariton Scattering (2)
To correct many-body
picture the phonon
renormalization of the
electron spectrum was
computed.
As a result of Quantum
Mechanical calculation
we obtain new
scattering rate :
scattering is averaged
near the vHs but it is
still a fast process.
q~1/l forward scattering
q~2k : backward scattering
for vF~108 cm/s
and wSO~140meV : l~40 nm
2ki ~ 2p/a ~ 1/nm
Remote SPP Scattering Rate
• for the SiO2 (quartz) substrate the RPS is likely prevailing over inelastic
scattering by NT (own) optical phonons for the small distance to the polar
substrate < l ~ 40 nm;
• the effect is even stronger for high-k dielectrics due to increase of the
Froehlich constant : x20 and more;
• the effect is independent of the radius of the NT, thus for narrow NTs it will
dominate over the other 1/R mechanisms
Remote SPP Scattering Rate
• scattering rate increases with the electric field strength because of stronger
warming of the electron distribution function
Remote SPP Scattering
• IVCs with and without taking into account SPP mechanism
The saturation regime
is clearly seen at larger
bias (larger field) for
SPP scattering
Inset: mobility vs. field
Remote SPP Scattering
• overheating of the channel : neglecting the thermal
sink in the leads
where
• two scattering mechanisms : SPP
phonons take the heat directly into
bulk substrate; NT phonons warm
the lattice but are inefficient
• Joule losses - IsF are for the total
energy loss; while NT phonons take
only a small fraction of that
Remote SPP Scattering
• ratio of "real"-to-expected
losses for two tubes (R~0.5 and
1.0 nm) at two to= 77 and 300K
• inset: data collapse for (linear)
dependence on the electron
concentration (0.1 and 0.2 e/nm)
• different temperature dependence
for two scattering mechanisms