* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Nearest Neighbour - Department of Computer Science
Survey
Document related concepts
Transcript
Supervised Clustering --Algorithms and Applications
Christoph F. Eick
Department of Computer Science
University of Houston
Organization of the Talk
1. Supervised Clustering
2. Representative-based Supervised Clustering Algorithms
3. Applications: Using Supervised Clustering for
a. Dataset Editing
b. Class Decomposition
c. Distance Function Learning
d. Region Discovery in Spatial Datasets
4. Other Activities I am Involved With
Ch. Eick: Supervised Clustering --- Algorithms and Applications
List of Persons that Contributed to the Work
Presented in Today’s Talk
• Tae-Wan Ryu (former PhD student; now faculty member Cal State
Fullerton)
• Ricardo Vilalta (colleague at UH since 2002; Co-Director of the UH’s
Data Mining and Knowledge Discovery Group)
• Murali Achari (former Master student)
• Alain Rouhana (former Master student)
• Abraham Bagherjeiran (current PhD student)
• Chunshen Chen (current Master student)
• Nidal Zeidat (current PhD student)
• Sujing Wang (current PhD student)
• Kim Wee (current MS student)
• Zhenghong Zhao (former Master student)
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Traditional Clustering
• Partition a set of objects into groups of similar objects.
Each group is called a cluster.
• Clustering is used to “detect classes” in a data set
(“unsupervised learning”).
• Clustering is based on a fitness function that relies on a
distance measure and usually tries to create “tight”
clusters.
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Ch. Eick
Different Forms of Clustering
Objectives Supervised Clustering: Minimize cluster impurity
while keeping the number of clusters low (expressed by a
fitness function q(X)).
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Motivation: Finding Subclasses using SC
Attribute1
Ford Trucks
:Ford
:GMC
GMC Trucks
GMC Van
Ford Vans
Ford SUV
GMC SUV
Attribute2
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Related Work Supervised Clustering
• Sinkkonen’s [SKN02] discriminative clustering and
Tishby’s information bottleneck method [TPB99, ST99]
can be viewed as probabilistic supervised clustering
algorithms.
• There has been a lot of work in the area of semisupervised clustering that centers on clustering with
background information. Although the focus of this work
is traditional clustering, there is still a lot of similarity
between techniques and algorithms they investigate and
the techniques and algorithms we investigate.
Ch. Eick: Supervised Clustering --- Algorithms and Applications
2. Representative-Based Supervised Clustering
• Aims at finding a set of objects among all objects (called
representatives) in the data set that best represent the
objects in the data set. Each representative corresponds
to a cluster.
• The remaining objects in the data set are then clustered
around these representatives by assigning objects to the
cluster of the closest representative.
Remark: The popular k-medoid algorithm, also called PAM,
is a representative-based clustering algorithm.
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Representative-Based Supervised Clustering …
(Continued)
Attribute1
2
1
3
4
Attribute2
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Representative-Based Supervised Clustering …
(continued)
Attribute1
2
1
3
4
Attribute2
Objective of RSC: Find a subset OR of O such that the clustering X
obtained by using the objects in OR as representatives minimizes q(X).
Ch. Eick: Supervised Clustering --- Algorithms and Applications
SC Algorithms Currently Investigated
1.
2.
3.
4.
5.
6.
Supervised Partitioning Around Medoids (SPAM).
Single Representative Insertion/Deletion Steepest Decent
Hill Climbing with Randomized Restart (SRIDHCR).
Top Down Splitting Algorithm (TDS).
Supervised Clustering using Evolutionary Computing (SCEC)
Agglomerative Hierarchical Supervised Clustering (AHSC)
Grid-Based Supervised Clustering (GRIDSC)
Remark: For a more detailed discussion of SCEC and SRIDHCR see [EZZ04]
Ch. Eick: Supervised Clustering --- Algorithms and Applications
A Fitness Function for Supervised Clustering
q(X) := Impurity(X) + β*Penalty(k)
where Impurity(X )
# of Minority Examples
,
n
k c
and Penalty(k) n
0
kc
k: number of clusters used
n: number of examples the dataset
c: number of classes in a dataset.
β: Weight for Penalty(k), 0< β ≤2.0
kc
Penalty(k)
Penalty(k) vs k
Penalty(k) increase sub-linearly.
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
0
5
10
26
k
53
because the effect of increasing the # of clusters
from k to k+1 has greater effect on the end result
when k is small than when it is large. Hence the
formula above
k
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Algorithm SRIDHCR (Greedy Hill Climbing)
REPEAT r TIMES
curr := a randomly created set of representatives (with size between c+1 and
2*c)
WHILE NOT DONE DO
1. Create new solutions S by adding a single non-representative to
curr and by removing a single representative from curr
2. Determine the element s in S for which q(s) is minimal (if there is
more than one minimal element, randomly pick one)
3. IF q(s)<q(curr) THEN curr:=s
ELSE IF q(s)=q(curr) AND |s|>|curr| THEN Curr:=s
ELSE terminate and return curr as the solution for this run.
Report the best out of the r solutions found.
Highlights:
• k is not an input parameter, SRIDHCR searches for best k
within the range that is induced by b.
• Reports the best clustering found in r runs
Ch. Eick: Supervised Clustering --- Algorithms and Applications
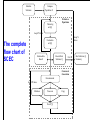
Supervised Clustering using Evolutionary Computing: SCEC
Initial generation
Next generation
Mutation
Crossover
Copy
Final generation
Best solution
Result:
Initialize
Initialize
Solutions
Solutions
Compose
Compose
Population
Population
S S
Evaluate
Evaluate
a a
Population
Population
Clustering
Clustering
onon
S[i]
S[i]
Loop
Loop
PSPS
times
times
The complete
complete
The
flow chart
chart of
of
flow
SCEC
SCEC
Loop
Loop
NN
times
times
Evaluation
Evaluation
onon
S[i]
S[i]
Intermediate
Intermediate
Result
Result
Record
Record
Best
Best
Solution,
Solution,
QQ
Exit
Exit
Best
Best
Solution,
Solution,
Q,Q,
Summary
Summary
Create
Create
next
next
Generation
Generation
K-tournament
K-tournament
Loop
Loop
PSPS
times
times
Mutation
Mutation
Crossover
Crossover
Copy
Copy
New
New
S’[i]
S’[i]
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Complex1 Dataset
Complex1-Reduced
500
450
Class-0
400
Class-1
350
Class-2
300
Class-3
Class-4
250
200
Class-5
150
Class-6
100
Class-7
50
Class-8
0
0
200
400
600
800
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Supervised Clustering Result
Complex-1-Reduced, SRIDHCR, Beta=0.25, r=50
500
450
400
350
300
250
200
150
100
50
0
0
100
200
300
400
500
600
700
800
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Supervised Clustering --Algorithms and Applications
Organization of the Talk
1. Supervised Clustering
2. Representative-based Supervised Clustering Algorithms
3. Applications: Using Supervised Clustering for
a. for Dataset Editing
b. for Class Decomposition
c. for Distance Function Learning
d. for Region Discovery in Spatial Datasets
4. Other Activities I am Involved With
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Nearest Neighbour Rule
Consider a two class problem
where each sample consists of
two measurements (x,y).
For a given query point q,
assign the class of the
nearest neighbour.
k=1
Compute the k nearest
neighbours and assign the
class by majority vote.
k=3
Problem: requires “good” distance function
Ch. Eick: Supervised Clustering --- Algorithms and Applications
3a. Dataset Reduction: Editing
• Training data may contain noise, overlapping classes
• Editing seeks to remove noisy points and produce smooth decision
boundaries – often by retaining points far from the decision
boundaries
• Main Goal of Editing: enhance the accuracy of classifier (% of
“unseen” examples classified correctly)
• Secondary Goal of Editing: enhance the speed of a k-NN classifier
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Wilson Editing
•
•
Wilson 1972
Remove points that do not agree with the majority of their k nearest neighbours
Earlier example
Original data
Wilson editing with k=7
Overlapping classes
Original data
Wilson editing with k=7
Ch. Eick: Supervised Clustering --- Algorithms and Applications
RSC Dataset Editing
Attribute1
A
Attribute1
B
D
C
F
E
Attribute2
a. Dataset clustered using
supervised clustering.
Attribute2
b. Dataset edited using cluster
representatives.
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Experimental Evaluation
• We compared a traditional 1-NN, 1-NN using Wilson Editing,
Supervised Clustering Editing (SCE), and C4.5 (that was run using
its default parameter setting).
• A benchmark consisting of 8 UCI datasets was used for this
purpose.
• Accuracies were computed using 10-fold cross validation.
• SRIDHCR was used for supervised clustering.
• SCE was tested using different compression rates by associating
different penalties with the number of clusters found (by setting
parameter b to: 0.1, 0.4 and 1.0).
• Compression rates of SCE and Wilson Editing were computed
using: 1-(k/n) with n being the size of the original dataset and k
being the size of the edited dataset.
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Table 2: Prediction Accuracy for the four classifiers.
β
NR
Wilson
1-NN
C4.5
0.636
0.589
0.575
0.607
0.607
0.607
0.692
0.692
0.692
0.677
0.677
0.677
0.796
0.833
0.838
0.804
0.804
0.804
0.767
0.767
0.767
0.782
0.782
0.782
0.736
0.736
0.745
0.734
0.734
0.734
0.690
0.690
0.690
0.745
0.745
0.745
0.667
0.667
0.665
0.716
0.716
0.716
0.700
0.700
0.700
0.723
0.723
0.723
0.755
0.793
0.809
0.809
0.809
0.809
0.783
0.783
0.783
0.802
0.802
0.802
0.834
0.841
0.837
0.796
0.796
0.796
0.768
0.768
0.768
0.781
0.781
0.781
0.947
0.973
0.953
0.936
0.936
0.936
0.947
0.947
0.947
0.947
0.947
0.947
0.938
0.919
0.890
0.966
0.966
0.966
0.956
0.956
0.956
0.968
0.968
0.968
Glass (214)
0.1
0.4
1.0
Heart-Stat Log (270)
0.1
0.4
1.0
Diabetes (768)
0.1
0.4
1.0
Vehicle (846)
0.1
0.4
1.0
Heart-H (294)
0.1
0.4
1.0
Waveform (5000)
0.1
0.4
1.0
Iris-Plants (150)
0.1
0.4
1.0
Segmentation (2100)
0.1
0.4
1.0
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Table 3: Dataset Compression Rates for SCE and Wilson Editing.
b
Glass (214)
0.1
0.4
1.0
Heart-Stat Log (270)
0.1
0.4
1.0
Diabetes (768)
0.1
0.4
1.0
Vehicle (846)
0.1
0.4
1.0
Heart-H (294)
0.1
0.4
1.0
Waveform (5000)
0.1
0.4
1.0
Iris-Plants (150)
0.1
0.4
1.0
Segmentation (2100)
0.1
0.4
1.0
Avg. k
[Min-Max]
for SCE
SCE
Compression
Rate (%)
Wilson
Compression
Rate (%)
34 [28-39]
25 [19-29]
6 [6 – 6]
84.3
88.4
97.2
27
27
27
15 [12-18]
2 [2 – 2]
2 [2 – 2]
94.4
99.3
99.3
22.4
22.4
22.4
27 [22-33]
9 [2-18]
2 [2 – 2]
96.5
98.8
99.7
30.0
30.0
30.0
57 [51-65]
38 [ 26-61]
14 [ 9-22]
97.3
95.5
98.3
30.5
30.5
30.5
14 [11-18]
2
2
95.2
99.3
99.3
21.9
21.9
21.9
104 [79-117]
28 [20-39]
4 [3-6]
97.9
99.4
99.9
23.4
23.4
23.4
4 [3-8]
3 [3 – 3]
3 [3 – 3]
97.3
98.0
98.0
6.0
6.0
6.0
57 [48-65]
30 [24-37]
14
97.3
98.6
99.3
2.8
2.8
2.8
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Summary SCE and Wilson Editing
• Wilson editing enhances the accuracy of a traditional 1-NN classifier
for six of the eight datasets tested. It achieved compression rates of
approx. 25%, but much lower compression rates for “easy” datasets.
• SCE achieved very high compression rates without loss in accuracy
for 6 of the 8 datasets tested.
• SCE accomplished a significant improvement in accuracy for 3 of the
8 datasets tested.
• Surprisingly, many UCI datasets can be compressed by just using a
single representative per class without a significant loss in accuracy.
• SCE tends to pick representatives that are in the center of a region
that is dominated by a single class; it removes examples that are
classified correctly as well as examples that are classified incorrectly
from the dataset. This explains its much higher compression rates.
Remark: For a more detailed evaluation of SCE, Wilson Editing, and
other editing techniques see [EZV04] and [ZWE05].
Ch. Eick: Supervised Clustering --- Algorithms and Applications
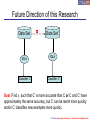
Future Direction of this Research
Data Set
IDLA
Classifier C
p
Data Set’
IDLA
Classifier C’
Goal: Find p, such that C’ is more accurate than C or C and C’ have
approximately the same accuracy, but C’ can be learnt more quickly
and/or C’ classifies new examples more quickly.
Ch. Eick: Supervised Clustering --- Algorithms and Applications
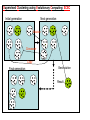
Supervised Clustering vs. Clustering the
Examples of Each Separately
Approaches to discover subclasses of a given class:
1. Cluster the examples of each class separately
2. Use supervised clustering
Figure 4. Supervised clustering editing vs. clustering each class (x and o) separately.
O
O
O
OOx
OOx
OOx
x
x
x
x
x
x
Remark: A traditional clustering algorithm, such as k-medoids, would pick o
as the cluster representative, because it is “blind” on how the examples of
other classes distribute, whereas supervised clustering would pick o as the
representative; obviously, o is not a good choice for editing, because it attracts
points of the class x, which leads to misclassifications.
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Applications of Supervised Clustering
3.b Class Decomposition (see also [VAE03])
Attribute 1
Attribute 1
Attribute 2
Attribute 2
Simple classifiers:
Attribute 1
• Encompass a small class of
approximating functions.
• Limited flexibility in their
decision boundaries
Attribute 2
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Naïve Bayes vs. Naïve Bayes with
Class Decomposition
Dataset
Diabetes
Heart-H
Segment
Vehicle
Naïve Bayes
(NB)
76.56
79.73
68.00
45.02
NB with Class
Decomposition
77.08
70.27
75.045
68.25
Improvement
0.52%
9.46%
7.05%
23.23%
Ch. Eick: Supervised Clustering --- Algorithms and Applications
3c. Using Clustering in Distance Function Learning
Example: How to Find Similar Patients?
The following relation is given (with 10000 tuples):
Patient(ssn, weight, height, cancer-sev, eye-color, age,…)
• Attribute Domains
– ssn: 9 digits
– weight between 30 and 650; mweight=158 sweight=24.20
– height between 0.30 and 2.20 in meters; mheight=1.52 sheight=19.2
– cancer-sev: 4=serious 3=quite_serious 2=medium 1=minor
– eye-color: {brown, blue, green, grey }
– age: between 3 and 100; mage=45 sage=13.2
Task: Define Patient Similarity
Ch. Eick: Supervised Clustering --- Algorithms and Applications
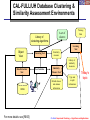
CAL-FULL/UH Database Clustering &
Similarity Assessment Environments
Library of
clustering algorithms
Training
Data
A set of
clusters
Learning
Tool
Object
View
Data Extraction
Tool
DBMS
For more details: see [RE05]
Clustering Tool
User Interface
Similarity
measure
Similarity
Measure Tool
Default choices
and domain
information
Library of
similarity
measures
Type and
weight
information
Today’s
topic
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Similarity Assessment Framework and Objectives
q (o , o )
i
j
p
qf (oi oj ) * wf
f 1
p
wf
f 1
,
• Objective: Learn a good distance function q for classification tasks.
• Our approach: Apply a clustering algorithm with the distance function q to
be evaluated that returns a number of clusters k. The more pure the
obtained clusters are the better is the quality of q.
• Our goal is to learn the weights of an object distance function q such that
all the clusters are pure (or as pure is possible); for more details see
[ERBV05] and [BECV05] papers.
Ch. Eick: Supervised Clustering --- Algorithms and Applications
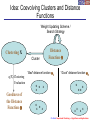
Idea: Coevolving Clusters and Distance
Functions
Weight Updating Scheme /
Search Strategy
Clustering X
Cluster
q(X) Clustering
Evaluation
Goodness of
the Distance
Function Q
Distance
Function Q
“Bad” distance function Q1
“Good” distance function Q2
o
o
x oox x
x
o
x o x
o
oo
o
o o
x
x
x
x
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Idea Inside/Outside Weight Updating
o:=examples belonging to majority class
x:= non-majority-class examples
Cluster1: distances with respect to Att1
xo oo ox
Action: Increase weight of Att1
Idea: Move examples of the
majority class closer to each other
Cluster1: distances with respect to Att2
o o xx o o
Action: Decrease weight for Att2
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Sample Run of IOWU for Diabetes Dataset
Graph produced by Abraham Bagherjeiran
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Research Framework Distance Function Learning
Weight-Updating Scheme /
Search Strategy
Distance Function
Evaluation
Inside/Outside
Weight Updating
K-Means
[ERBV04]
Randomized
Hill Climbing
Other
Research
[BECV05]
Adaptive
Clustering
…
Supervised
Clustering
Work
By Karypis
NN-Classifier
…
Ch. Eick: Supervised Clustering --- Algorithms and Applications
3.d Discovery of Interesting Regions for
Spatial Data Mining
Task: 2D/3D datasets are given; discover interesting regions
in the dataset that maximize a given fitness function;
examples of region discovery include:
– Discover regions that have significant deviations from
the prior probability of a class; e.g. regions in the state of
Wyoming were people are very poor or not poor at all
– Discover regions that have significant variation in the
income (fitness is defined based on the variance with
respect to income in a region)
– Discover regions for congressional redistricting
– Discover congested regions for traffic control
Remark: We use (supervised) clustering to discover such
regions; regions are implicitly defined by the set of points
that belong to a cluster.
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Wyoming Map
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Household Income in 1999: Wyoming Park County
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Clusters Regions
Example: 2 clusters in red and blue are given; regions are defined by using a Voronoi
diagram based on a NN classifier with k=7; region are in grey and white.
Ch. Eick: Supervised Clustering --- Algorithms and Applications
An Evaluation Scheme for Discovering Regions
that Deviate from the Prior Probability of a Class C
Let
prior(C)= |C|/n
p(c,C)= percentage of examples in c that belong to class C
Reward(c) is computed based on p(c.C), prior(C) , and based on the following
parameters: g1,g2,R+,R (g11g2; R+,R0) relying on the following interpolation
function (e.g. g1=0.8,g2=1.2,R+ =1, R=1):
qC(X)= cX (t(p(c,C),prior(C),g1,g2,R+,R-) *|c|)b/n)
with b>1 (typically, 1.0001<b<2); the idea is that increases in
cluster-size rewarded nonlinearly, favoring clusters with
more points as long as |c|*t(…) increases.
Reward(c)
R+
R
t(p(C),prior(C),g1,g2,R+,R)
prior(C)*g1
prior(C)
prior(C)*g2
1
p(c,C)
Ch. Eick
Example: Discovery of “Interesting Regions”
in Wyoming Census 2000 Datasets
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Supervised Clustering --Algorithms and Applications
Organization of the Talk
1. Supervised Clustering
2. Representative-based Supervised Clustering Algorithms
3. Applications: Using Supervised Clustering for
a. for Dataset Editing
b. for Class Decomposition
c. for Distance Function Learning
d. for Region Discovery in Spatial Datasets
4. Other Activities I am Involved With
Ch. Eick: Supervised Clustering --- Algorithms and Applications
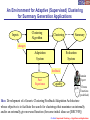
An Environment for Adaptive (Supervised) Clustering
for Summary Generation Applications
Inputs
Clustering
Algorithm
Clustering
Summary
changes
Adaptation
System
Evaluation
System
feedback
Past
Experience
quality
Domain
Expert
q(X), Fitness
… Functions
(predefined)
Idea: Development of a Generic Clustering/Feedback/Adaptation Architecture
whose objective is to facilitate the search for clusterings that maximize an internally
and/or an externally given reward function (for some initial ideas see [BECV05])
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Clustering Algorithm Inputs
Data Set Examples
Data Set Feature Representation
Distance Function
Clustering Algorithm Parameters
Fitness Function Parameters
Background Knowledge
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Research Topics 2005/2006
•
•
•
•
•
•
•
Inductive Learning/Data Mining
– Decision trees, nearest neighbor classifiers
– Using clustering to enhance classification algorithms
– Making sense of data
Supervised Clustering
– Learning subclasses
– Supervised clustering algorithms that learn clusters with arbitrary shape
– Using supervised clustering for region discovery
– Adaptive clustering
Tools for Similarity Assessment and Distance Function Learning
Data Set Compression and Creating Meta Knowledge for Local Learning Techniques
– Comparative studies
– Creating maps and other data set signatures for datasets based on editing, SC, and
other techniques
Traditional Clustering
Data Mining and Information Retrieval for Structured Data
Other: Evolutionary Computing, File Prediction, Ontologies, Heuristic Search,
Reinforcement Learning, Data Models.
Remark: Topics that were “covered” in this talk are in blue
Ch. Eick: Supervised Clustering --- Algorithms and Applications
Links to 7 Papers
[VAE03] R. Vilalta, M. Achari, C. Eick, Class Decomposition via Clustering: A New Framework for Low-Variance
Classifiers, in Proc. IEEE International Conference on Data Mining (ICDM), Melbourne, Florida, November
2003.
http://www.cs.uh.edu/~ceick/kdd/VAE03.pdf
[EZZ04] C. Eick, N. Zeidat, Z. Zhao, Supervised Clustering --- Algorithms and Benefits, short version appeared
in Proc. International Conference on Tools with AI (ICTAI), Boca Raton, Florida, November 2004.
http://www.cs.uh.edu/~ceick/kdd/EZZ04.pdf
[EZV04] C. Eick, N. Zeidat, R. Vilalta, Using Representative-Based Clustering for Nearest Neighbor Dataset
Editing, in Proc. IEEE International Conference on Data Mining (ICDM), Brighton, England, November 2004.
http://www.cs.uh.edu/~ceick/kdd/EZV04.pdf
[RE05] T. Ryu and C. Eick, A Clustering Methodology and Tool, in Information Sciences 171(1-3): 29-59 (2005).
http://www.cs.uh.edu/~ceick/kdd/RE05.doc
[ERBV04] C. Eick, A. Rouhana, A. Bagherjeiran, R. Vilalta, Using Clustering to Learn Distance Functions for
Supervised Similarity Assessment, in Proc. MLDM'05, Leipzig, Germany, July 2005.
http://www.cs.uh.edu/~ceick/kdd/ERBV05.pdf
[ZWE05] N. Zeidat, S. Wang, C. Eick,, Editing Techniques: a Comparative Study, submitted for publication.
http://www.cs.uh.edu/~ceick/kdd/ZWE05.pdf
[BECV05] A. Bagherjeiran, C. Eick, C.-S. Chen, R. Vilalta, Adaptive Clustering: Obtaining Better Clusters Using
Feedback and Past Experience, submitted for publication.
http://www.cs.uh.edu/~ceick/kdd/BECV05.pdf
Ch. Eick: Supervised Clustering --- Algorithms and Applications