* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Stats 241.3 Term Test 4 - Mathematics and Statistics
Survey
Document related concepts
Transcript
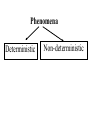
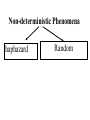
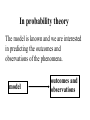
Stats 241.3 Term Test 4 Solutions I. Suppose X and Y are two discrete random variables having joint probability function p(x,y) given in the following table: a) Find the marginal probability function of X, px(x). b) Find the marginal probability function of Y, py(y). x\y 1 2 3 4 Total pX(x) 1 1 0 0 0 3 12 36 1 5 1 2 0 12 9 36 12 36 1 1 5 3 0 10 9 36 36 36 1 1 1 4 0 11 9 12 9 36 Total pY(y) 15 1 9 8 4 36 36 36 36 c) a) Compute E[XY]. 4 4 3 0 0 0 (1 2) (1 3) (1 4) 36 36 36 36 4 5 3 0 (2 1) (2 2) (2 3) (2 4) 36 36 36 36 4 1 5 0 (3 1) (3 2) (3 3) (3 4) 36 36 36 36 4 3 0 4 (4 1) (4 2) (4 3) (4 4) 36 36 36 36 3 8 20 18 12 6 45 16 24 64 216 6 36 36 E XY xyp x, y (11) x 1 y 1 a) Determine the distribution of W = X – Y d) Solution: The possible values of W are w = -3, -2, -1, 0, 1, 2, 3 (the cells in the table where W = w are illustrated below with the same colour. x\y 1 1 1 12 1 9 1 9 1 9 2 3 4 Thus the distribution of W is: -3 -2 -1 w pW(w) 0 36 0 36 3 36 2 0 3 0 4 0 5 36 1 36 1 12 1 12 5 36 0 0 0 17 36 1 5 36 0 1 9 2 7 36 3 4 36 II. Show that if X and Y are independent and that each have a binomial distribution with paramaters n and p then W = X + Y has a binomial distribution with parameters 2n and p. Solution: (Using moment generating functions) mX(t) = mY(t) = [q + pet]n Hence mX + Y(t) = mX (t)mY(t) = [q + pet]n [q + pet]n = [q + pet]2n = mgf of binomial distribution with parameters 2n and p. An alternative solution is to use the probability mass function n x n x n y n y pX x p q and pY y p q x y and n x n x n y n y p x, y p X x pY y p q p q x y n n x y 2 n x y p q x y y x 0 1 2 0 p(0, 0) p(1, 0) p(2, 0) 1 p(0, 1) p(1, 1) p(2, 1) 2 p(0, 2) p(1, 2) p(2, 2) n p(0, n) p(1, n) p(2, n) n p(n, 0) p(n, 1) p(n, 2) p(n, n) P X Y w p w,0 p w 1,1 p 0, w n n w 2 n w p q i 0 i w i w 2n w 2 n w p q w III. A rectifier following a square law has the characteristic Y = kX2, x > 0, where X and Y are the input and output voltages, respectively. If the input to the rectifier is noise with the probability density function 2 2x e x 0 x f ( x) 0 otherwise Find the probability density function of the output Y (Note: >0). Solution: The cumulative distribution function of Y is: G y P Y y P kX 2 y P X 2 ky P ky X y k 2 2x x e y k dx 0 Hence ky d g y G y dy 0 2x e x 2 dx 2 y k e y k d dy y k 2 y k y k 1 e 2 y k Thus the distribution of Y is exponential with parameter 1 k 12 1 y k e if y 0 k Probability has many applications in many areas • Medicine – Modeling epidemics – Modeling disease progression • Engineering – Reliability design electrical systems • Economics – Modeling of financial time series, economic time series – Determining Risk Statistics What is Statistics? It is the major mathematical tool of scientific inference – methods for drawing conclusion from data. Data that is to some extent corrupted by some component of random variation (random noise) Phenomena Deterministic Non-deterministic Deterministic Phenomena A mathematical model exists that allows accurate prediction of outcomes of the phenomena (or observations taken from the phenomena) Non-deterministic Phenomena Lack of perfect predictability Non-deterministic Phenomena haphazard Random Random Phenomena No mathematical model exists that allows accurate prediction of outcomes of the phenomena (or observations) However the outcomes (or observations) exhibit in the long run on the average statistical regularity In both Statistics and Probability theory we are concerned with studying random phenomena In probability theory The model is known and we are interested in predicting the outcomes and observations of the phenomena. model outcomes and observations In statistics The model is unknown the outcomes and observations of the phenomena have been observed. We are interested in determining the model from the observations outcomes and observations model Example - Probability A coin is tossed n = 100 times We are interested in the observation, X, the number of times the coin is a head. Assuming the coin is balanced (i.e. p = the probability of a head = ½.) 100 1 x 1 100 x p x P X x 2 2 x 100 1 100 for x 0, 1, , 100 2 x Example - Statistics We are interested in the success rate, p, of a new surgical procedure. The procedure is performed n = 100 times. X, the number of successful times the procedure is performed is 82. The success rate p is unknown. If the success rate p was known. Then 100 x 100 x p x P X x p 1 p x This equation allows us to predict the value of the observation, X. In the case when the success rate p was unknown. Then the following equation is still true the success rate 100 x 100 x p x P X x p 1 p x We will want to use the value of the observation, X = 82 to make a decision regarding the value of p. Introductory Statistics Courses Non calculus Based Stats 244.3 Stats 245.3 Calculus Based Stats 242.3 Stats 244.3 Statistical concepts and techniques including graphing of distributions, measures of location and variability, measures of association, regression, probability, confidence intervals, hypothesis testing. Students should consult with their department before enrolling in this course to determine the status of this course in their program. Prerequisite(s): A course in a social science or Mathematics A30. Stats 245.3 An introduction to basic statistical methods including frequency distributions, elementary probability, confidence intervals and tests of significance, analysis of variance, regression and correlation, contingency tables, goodness of fit. Prerequisite(s): MATH 100, 101, 102, 110 or STAT 103. Stats 242.3 Sampling theory, estimation, confidence intervals, testing hypotheses, goodness of fit, analysis of variance, regression and correlation. Prerequisite(s):MATH 110, 116 and STAT 241. Stats 244 and 245 • do not require a calculus prerequisite • are Recipe courses Stats 242 • does require calculus and probability (Stats 241) as a prerequisite • More theoretical class – You learn techniques for developing statistical procedures and thoroughly investigating the properties of these procedures Statistics Courses beyond Stats 242.3 STAT 341.3 Probability and Stochastic Processes 1/2(3L-1P) Prerequisite(s): STAT 241. Random variables and their distributions; independence; moments and moment generating functions; conditional probability; Markov chains; stationary time-series. STAT 342.3 Mathematical Statistics 1(3L-1P) Prerequisite(s): MATH 225 or 276; STAT 241 and 242. Probability spaces; conditional probability and independence; discrete and continuous random variables; standard probability models; expectations; moment generating functions; sums and functions of random variables; sampling distributions; asymptotic distributions. Deals with basic probability concepts at a moderately rigorous level. Note: Students with credit for STAT 340 may not take this course for credit. STAT 344.3 Applied Regression Analysis 1/2(3L-1P) Prerequisite(s): STAT 242 or 245 or 246 or a comparable course in statistics. Applied regression analysis involving the extensive use of computer software. Includes: linear regression; multiple regression; stepwise methods; residual analysis; robustness considerations; multicollinearity; biased procedures; nonlinear regression. Note: Students with credit for ECON 404 may not take this course for credit. Students with credit for STAT 344 will receive only half credit for ECON 404. STAT 345.3 Design and Analysis of Experiments 1/2(3L-1P) Prerequisite(s): STAT 242 or 245 or 246 or a comparable course in statistics. An introduction to the principles of experimental design and analysis of variance. Includes: randomization, blocking, factorial experiments, confounding, random effects, analysis of covariance. Emphasis will be on fundamental principles and data analysis techniques rather than on mathematical theory. STAT 346.3 Multivariate Analysis 1/2(3L-1P) Prerequisite(s): MATH 266, STAT 241, and 344 or 345. The multivariate normal distribution, multivariate analysis of variance, discriminant analysis, classification procedures, multiple covariance analysis, factor analysis, computer applications. STAT 347.3 Non Parametric Methods 1/2(3L-1P) Prerequisite(s): STAT 242 or 245 or 246 or a comparable course in statistics. An introduction to the ideas and techniques of non-parametric analysis. Includes: one, two and K samples problems, goodness of fit tests, randomness tests, and correlation and regression. STAT 348.3 Sampling Techniques 1/2(3L-1P) Prerequisite(s): STAT 242 or 245 or 246 or a comparable course in statistics. Theory and applications of sampling from finite populations. Includes: simple random sampling, stratified random sampling, cluster sampling, systematic sampling, probability proportionate to size sampling, and the difference, ratio and regression methods of estimation. STAT 349.3 Time Series Analysis 1/2(3L-1P) Prerequisite(s): STAT 241, and 344 or 345. An introduction to statistical time series analysis. Includes: trend analysis, seasonal variation, stationary and non-stationary time series models, serial correlation, forecasting and regression analysis of time series data. STAT 442.3 Statistical Inference 2(3L-1P) Prerequisite(s): STAT 342. Parametric estimation, maximum likelihood estimators, unbiased estimators, UMVUE, confidence intervals and regions, tests of hypotheses, Neyman Pearson Lemma, generalized likelihood ratio tests, chi-square tests, Bayes estimators. STAT 443.3 Linear Statistical Models 2(3L-1P) Prerequisite(s): MATH 266, STAT 342, and 344 or 345. A rigorous examination of the general linear model using vector space theory. Includes: generalized inverses; orthogonal projections; quadratic forms; Gauss-Markov theorem and its generalizations; BLUE estimators; Non-full rank models; estimability considerations.