Download Stats 241.3 Term Test 4 - Mathematics and Statistics

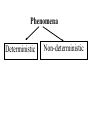
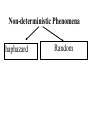
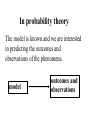
Stats 241.3 Term Test 4
Solutions
I. Suppose X and Y are two discrete random variables having joint probability
function p(x,y) given in the following table:
a) Find the marginal probability function of X, px(x).
b) Find the marginal probability function of Y, py(y).
x\y
1
2
3
4
Total pX(x)
1
1
0
0
0
3
12
36
1
5
1
2
0
12
9
36 12
36
1
1
5
3
0
10
9
36 36
36
1
1
1
4
0
11
9
12
9
36
Total pY(y) 15
1
9
8
4
36 36 36 36
c)
a) Compute E[XY].
4
4
3
0
0
0
 (1  2)  (1  3)  (1  4)
36
36
36
36
4
5
3
0
(2 1)  (2  2)  (2  3)  (2  4)
36
36
36
36
4
1
5
0
(3 1)  (3  2)  (3  3)  (3  4)
36
36
36
36
4
3
0
4
(4 1)  (4  2)  (4  3)  (4  4)
36
36
36
36
3  8  20  18  12  6  45  16  24  64 216


6
36
36
E  XY    xyp  x, y   (11)
x 1 y 1
a) Determine the distribution of W = X – Y
d)
Solution: The possible values of W are w = -3, -2, -1, 0, 1, 2, 3 (the cells in the table
where W = w are illustrated below with the same colour.
x\y
1
1
1
12
1
9
1
9
1
9
2
3
4
Thus the distribution of W is:
-3 -2 -1
w
pW(w)
0
36
0
36
3
36
2
0
3
0
4
0
5
36
1
36
1
12
1
12
5
36
0
0
0
17
36
1
5
36
0
1
9
2
7
36
3
4
36
II.
Show that if X and Y are independent and that each have a binomial distribution
with paramaters n and p then W = X + Y has a binomial distribution with parameters
2n and p.
Solution: (Using moment generating functions) mX(t) = mY(t) = [q + pet]n
Hence mX + Y(t) = mX (t)mY(t) = [q + pet]n [q + pet]n = [q + pet]2n = mgf of binomial
distribution with parameters 2n and p.
An alternative solution is to use the probability mass function
 n  x n x
 n  y n y
pX  x     p q
and pY  y     p q
 x
 y
and
 n  x n x  n  y n y
p  x, y   p X  x  pY  y     p q   p q
 x
 y
 n  n  x  y 2 n  x  y
    p q
 x  y 
y
x
0
1
2
0
p(0, 0)
p(1, 0)
p(2, 0)
1
p(0, 1)
p(1, 1)
p(2, 1)
2
p(0, 2)
p(1, 2)
p(2, 2)
n
p(0, n)
p(1, n)
p(2, n)
n
p(n, 0)
p(n, 1)
p(n, 2)
p(n, n)
P  X  Y  w  p  w,0  p  w 1,1 
 p  0, w
 n  n  w 2 n  w
   
p q
i  0  i  w  i 
w
 2n  w 2 n  w
 p q
w
III. A rectifier following a square law has the characteristic Y = kX2, x > 0, where X and
Y are the input and output voltages, respectively. If the input to the rectifier is noise
with the probability density function
2

 2x e  x  
0 x
f ( x)  

0
otherwise

Find the probability density function of the output Y (Note:  >0).
Solution: The cumulative distribution function of Y is:
G  y   P Y  y   P  kX 2  y   P  X 2  ky   P   ky  X 

y
k


2
2x x 

e
y
k


dx
0
Hence
 ky
d
g  y   G  y    
dy  0

2x

e
x
2


dx  


2

y
k
e
 y k
d
dy
y
k

2

y
k
 y k 1
e
2 y
k
Thus the distribution of Y is exponential with parameter  
1
k
 12

1  y k
e
if y  0
k
Probability
has many applications in many areas
• Medicine
– Modeling epidemics
– Modeling disease progression
• Engineering
– Reliability design electrical systems
• Economics
– Modeling of financial time series, economic time
series
– Determining Risk
Statistics
What is Statistics?
It is the major mathematical tool of
scientific inference – methods for
drawing conclusion from data.
Data that is to some extent corrupted
by some component of random
variation (random noise)
Phenomena
Deterministic
Non-deterministic
Deterministic Phenomena
A mathematical model exists that
allows accurate prediction of
outcomes of the phenomena (or
observations taken from the
phenomena)
Non-deterministic Phenomena
Lack of perfect predictability
Non-deterministic Phenomena
haphazard
Random
Random Phenomena
No mathematical model exists that allows
accurate prediction of outcomes of the
phenomena (or observations)
However the outcomes (or observations)
exhibit in the long run on the average
statistical regularity
In both Statistics and Probability theory
we are concerned with studying random
phenomena
In probability theory
The model is known and we are interested
in predicting the outcomes and
observations of the phenomena.
model
outcomes and
observations
In statistics
The model is unknown
the outcomes and observations of the
phenomena have been observed.
We are interested in determining the model
from the observations
outcomes and
observations
model
Example - Probability
A coin is tossed n = 100 times
We are interested in the observation, X, the
number of times the coin is a head.
Assuming the coin is balanced (i.e. p = the
probability of a head = ½.)
  
100  1 x 1 100 x
p  x   P  X  x  
 2
2
x


100  1 100

for x  0, 1, , 100
 2
 x 
 
Example - Statistics
We are interested in the success rate, p, of a
new surgical procedure.
The procedure is performed n = 100 times.
X, the number of successful times the
procedure is performed is 82.
The success rate p is unknown.
If the success rate p was known.
Then
100  x
100  x
p  x   P  X  x  
 p 1  p 
 x 
This equation allows us to predict the
value of the observation, X.
In the case when the success rate p was
unknown.
Then the following equation is still true the
success rate
100  x
100  x
p  x   P  X  x  
 p 1  p 
 x 
We will want to use the value of the
observation, X = 82 to make a decision
regarding the value of p.
Introductory Statistics Courses
Non calculus Based
Stats 244.3
Stats 245.3
Calculus Based
Stats 242.3
Stats 244.3
Statistical concepts and techniques including
graphing of distributions,
measures of location and variability,
measures of association,
regression,
probability,
confidence intervals,
hypothesis testing.
Students should consult with their department before
enrolling in this course to determine the status of this
course in their program.
Prerequisite(s):
A course in a social science or Mathematics A30.
Stats 245.3
An introduction to basic statistical methods
including frequency distributions, elementary
probability, confidence intervals and tests of
significance, analysis of variance, regression
and correlation, contingency tables, goodness
of fit.
Prerequisite(s):
MATH 100, 101, 102, 110 or STAT 103.
Stats 242.3
Sampling theory, estimation, confidence intervals,
testing hypotheses, goodness of fit,
analysis of variance,
regression and correlation.
Prerequisite(s):MATH 110, 116 and STAT 241.
Stats 244 and 245
• do not require a calculus prerequisite
• are Recipe courses
Stats 242
• does require calculus and probability (Stats
241) as a prerequisite
• More theoretical class – You learn
techniques for developing statistical
procedures and thoroughly investigating
the properties of these procedures
Statistics Courses beyond
Stats 242.3
STAT 341.3
Probability and Stochastic Processes
1/2(3L-1P)
Prerequisite(s): STAT 241.
Random variables and their distributions;
independence; moments and moment generating
functions; conditional probability; Markov
chains; stationary time-series.
STAT 342.3
Mathematical Statistics
1(3L-1P)
Prerequisite(s): MATH 225 or 276; STAT 241 and 242.
Probability spaces; conditional probability and
independence; discrete and continuous random variables;
standard probability models; expectations; moment
generating functions; sums and functions of random
variables; sampling distributions; asymptotic distributions.
Deals with basic probability concepts at a moderately
rigorous level.
Note: Students with credit for STAT 340 may not take this
course for credit.
STAT 344.3
Applied Regression Analysis
1/2(3L-1P)
Prerequisite(s): STAT 242 or 245 or 246 or a comparable
course in statistics.
Applied regression analysis involving the extensive use of
computer software. Includes: linear regression; multiple
regression; stepwise methods; residual analysis; robustness
considerations; multicollinearity; biased procedures; nonlinear regression.
Note: Students with credit for ECON 404 may not take this
course for credit. Students with credit for STAT 344 will
receive only half credit for ECON 404.
STAT 345.3
Design and Analysis of Experiments
1/2(3L-1P)
Prerequisite(s): STAT 242 or 245 or 246 or a
comparable course in statistics.
An introduction to the principles of experimental
design and analysis of variance. Includes:
randomization, blocking, factorial experiments,
confounding, random effects, analysis of covariance.
Emphasis will be on fundamental principles and
data analysis techniques rather than on
mathematical theory.
STAT 346.3
Multivariate Analysis
1/2(3L-1P)
Prerequisite(s): MATH 266, STAT 241, and
344 or 345.
The multivariate normal distribution,
multivariate analysis of variance,
discriminant analysis, classification
procedures, multiple covariance analysis,
factor analysis, computer applications.
STAT 347.3
Non Parametric Methods
1/2(3L-1P)
Prerequisite(s): STAT 242 or 245 or 246 or a
comparable course in statistics.
An introduction to the ideas and techniques of
non-parametric analysis. Includes: one, two
and K samples problems, goodness of fit tests,
randomness tests, and correlation and
regression.
STAT 348.3
Sampling Techniques
1/2(3L-1P)
Prerequisite(s): STAT 242 or 245 or 246 or a
comparable course in statistics.
Theory and applications of sampling from finite
populations. Includes: simple random sampling,
stratified random sampling, cluster sampling,
systematic sampling, probability proportionate to
size sampling, and the difference, ratio and
regression methods of estimation.
STAT 349.3
Time Series Analysis
1/2(3L-1P)
Prerequisite(s): STAT 241, and 344 or 345.
An introduction to statistical time series
analysis. Includes: trend analysis, seasonal
variation, stationary and non-stationary time
series models, serial correlation, forecasting
and regression analysis of time series data.
STAT 442.3
Statistical Inference
2(3L-1P)
Prerequisite(s): STAT 342.
Parametric estimation, maximum likelihood
estimators, unbiased estimators, UMVUE,
confidence intervals and regions, tests of
hypotheses, Neyman Pearson Lemma,
generalized likelihood ratio tests, chi-square
tests, Bayes estimators.
STAT 443.3
Linear Statistical Models
2(3L-1P)
Prerequisite(s): MATH 266, STAT 342, and 344 or
345.
A rigorous examination of the general linear model
using vector space theory. Includes: generalized
inverses; orthogonal projections; quadratic forms;
Gauss-Markov theorem and its generalizations;
BLUE estimators; Non-full rank models;
estimability considerations.