* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download File
Solar micro-inverter wikipedia , lookup
Public address system wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Flip-flop (electronics) wikipedia , lookup
Electrical ballast wikipedia , lookup
Electrical substation wikipedia , lookup
Negative feedback wikipedia , lookup
Audio power wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Power inverter wikipedia , lookup
Oscilloscope history wikipedia , lookup
Stray voltage wikipedia , lookup
Alternating current wikipedia , lookup
Current source wikipedia , lookup
Power MOSFET wikipedia , lookup
Voltage optimisation wikipedia , lookup
Mains electricity wikipedia , lookup
Two-port network wikipedia , lookup
Power electronics wikipedia , lookup
Integrating ADC wikipedia , lookup
Voltage regulator wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Current mirror wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Buck converter wikipedia , lookup
Vcc cannot exceed 5 V
Vin cannot be negative
𝑉𝐵𝐸 = 0.7𝑉
𝑉𝑜𝑢𝑡 = 𝑉𝑐𝑐 −
𝛽𝑅𝐶
(𝑉 − 0.7)
𝑅𝐵 𝑖𝑛
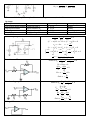
Amplifiers
input terminal, output terminal, both referenced to a
common reference (ground) – Vref, GND
Vpos, Vsupply, or VCC, or VDD.
Vneg, Vss, or VEE
They are also known as the rails of an amplifier.
Made with resistors, capacitors, and transistors.
Real voltage amplifiers
1. Input current is nonzero, which mean it has a
finite power gain. This input current leads to a
loading effect, because the input voltage of the
amplifier is now smaller than the source voltage if
the source has any resistance.
2. Output voltage will vary if the loading at the
output varies. The putout can amplify a range of
load resistances.
3. The output voltage is also limited range, cannot
exceed positive/negative supply rails.
Rin = vin / Iin
Rout = vout / Iout
𝐴𝑒𝑓𝑓 =
𝑅𝑖𝑛
𝑅𝐿
𝐴𝑣
𝑅𝑖𝑛 + 𝑅𝑠 𝑅𝑜𝑢𝑡 + 𝑅𝐿
When several ideal amplifiers are placed in cascade, the gain increases, Av= Av1*Av2…
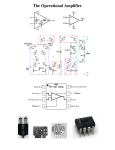
Op Amps
Op Amp Characteristics
Linear input-output response
High input resistance
Low output resistance
Very high gain
Nonideal op-amp
Inverting amplifier
Non-inverting amplifier
Voltage follower
Parameter
Open-loop gain A
Input resistance Ri
Output resistance Ro
Supply voltage Vcc
Typical Range
104 to 108
106 to 1013
1 to 100
5 to 24 V
Ideal Op Amp
Infinity
Infinity
0
As specified
𝑣 − − 𝑣0 𝑣 − 𝑣 − − 𝑣𝑠
+
+
=0
𝑅2
𝑅𝑖𝑛
𝑅1
(𝑣 − − 𝑣0 )𝐺2 + 𝑣 − 𝐺𝑖𝑛 + (𝑣 − − 𝑣𝑠 )𝐺1 = 0
−𝑣 0
𝑣0 = −𝐴𝑣 −
𝑣− =
𝐴
(𝑣 − − 𝑣0 )𝐺2 + 𝑣 − 𝐺𝑖𝑛 + (𝑣 − − 𝑣𝑠 )𝐺1 = 0
−𝑣 0
−𝑣 0
−𝑣 0
(
− 𝑣0 ) 𝐺2 +
𝐺 +(
− 𝑣𝑠 ) 𝐺1 = 0
𝐴
𝐴 𝑖𝑛
𝐴
𝑣0
𝐴𝐺1
=−
𝑠
𝑣
𝐺2 (𝐴 + 1) + 𝐺𝑖𝑛 + 𝐺1
𝑉0 − 𝑉𝑖𝑛 𝑉0 − 𝑉𝑜𝑢𝑡
𝑛𝑜𝑑𝑎𝑙 𝑎𝑡 𝑉0 :
+
=0
𝑅𝑖𝑛
𝑅𝑓
𝑉0 = 𝑉𝐺𝑁𝐷 = 0
−𝑉𝑖𝑛 −𝑉𝑜𝑢𝑡
+
=0
𝑅𝑖𝑛
𝑅𝑓
𝑅𝑓
𝑉𝑜𝑢𝑡 = −
∗𝑉
𝑅𝑖𝑛 𝑖𝑛
𝑅𝑓
𝐺𝑎𝑖𝑛 = −
𝑅𝑖𝑛
𝑉0 𝑉0 − 𝑉𝑜𝑢𝑡
+
=0
𝑅1
𝑅2
𝑉0 = 𝑉𝑖𝑛
𝑉𝑖𝑛 𝑉𝑖𝑛 − 𝑉𝑜𝑢𝑡
+
=0
𝑅1
𝑅2
𝑉𝑖𝑛 𝑉𝑖𝑛 𝑉𝑜𝑢𝑡
+
=
𝑅1 𝑅2
𝑅2
𝑉𝑜𝑢𝑡
𝑅2
𝐺𝑎𝑖𝑛 =
=1+
𝑉𝑖𝑛
𝑅1
𝑉𝑜𝑢𝑡 = 𝑉𝑖𝑛
𝑛𝑜𝑑𝑎𝑙 𝑎𝑡 𝑉0 :
𝑉0 𝑉0 − 𝑉2
+
=0
𝑅𝑔
𝑅2
𝑅𝑔 + 𝑅2
𝑉2
1
1
= 𝑉0 ( + ) = 𝑉0 (
)
𝑅2
𝑅𝑔 𝑅2
𝑅𝑔 𝑅2
𝑅𝑔
𝑉0 = 𝑉2
𝑅𝑔 + 𝑅2
𝑉0 − 𝑉1 𝑉0 − 𝑉𝑜𝑢𝑡
+
=0
𝑅1
𝑅𝑓
𝑅𝑔
1
1
𝑉1 𝑉𝑜𝑢𝑡
𝑉2
( + )−
=
𝑅𝑔 + 𝑅2 𝑅1 𝑅𝑓
𝑅1
𝑅𝑓
𝑅𝑔 𝑅𝑓 + 𝑅1
𝑅𝑓
𝑉𝑜𝑢𝑡 = 𝑉2
− 𝑉1
𝑅𝑔 + 𝑅2 𝑅1
𝑅1
𝑉1 𝑉2
𝑉𝑛
𝑉𝑜𝑢𝑡 = −𝑅𝑓 ( +
+ ⋯+ )
𝑅1 𝑅2
𝑅𝑛
If 𝑅1 = 𝑅2 = ⋯ = 𝑅𝑛
𝑅𝑓
𝑉𝑜𝑢𝑡 = − (𝑉1 + 𝑉2 + ⋯ + 𝑉𝑛 )
𝑅1
If 𝑅1 = 𝑅2 = ⋯ = 𝑅𝑛 = 𝑅𝑓
𝑉𝑜𝑢𝑡 = −(𝑉1 + 𝑉2 + ⋯ + 𝑉𝑛 )
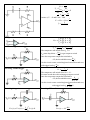
Difference amplifier
Summing amplifier
Output is inverted
Instrumentation amplifier
𝑉𝑜𝑢𝑡 =
Low pass passive filter
𝑅4 𝑅1 + 𝑅2 + 𝑅3
(𝑉2 − 𝑉1 )
𝑅5
𝑅2
High pass passive filter
𝟏
𝒇𝒄 = 𝟐𝝅𝑹𝑪
Low pass active filter
𝒇𝒄 =
𝟏
𝟐𝝅𝑹𝑪
Low pass active filter
𝟏
𝒇𝒄 = 𝟐𝝅𝑹
𝟐𝑪
𝒇𝒄 =
𝟏
𝟐𝝅𝑹𝟏 𝑪
𝑉𝑜𝑢𝑡
2
𝑉− − 𝑉𝑜𝑢𝑡
𝑑𝑉−
+𝐶
=0
𝑅
𝑑𝑡
𝑑𝑉− 𝑉−
𝑉𝑜𝑢𝑡
+
=
𝑑𝑡 𝑅𝐶
𝑅𝐶
At time t, V- = 0 and Vout = Vdd
Relaxation oscillator
𝑉+ =
𝑡
𝑉− = 𝑉𝑜𝑢𝑡 − 𝑉𝑑𝑑 𝑒 −𝑅𝐶
1
𝑓=
2 ln 3 𝑅𝐶
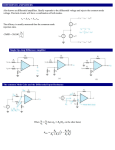
Comparator
𝑉𝑜𝑢𝑡
Non-inverting Schmitt trigger
Inverting Schmitt trigger
Inverting integrator
𝑉𝑜𝑢𝑡 (𝑡) = 𝑉𝑜𝑢𝑡 (𝑡0 ) −
𝑉𝑆+ 𝑖𝑓 𝑉1 > 𝑉2
= {𝑉𝑆− |𝑖𝑓 𝑉1 < 𝑉2}
0 𝑖𝑓 𝑉1 = 𝑉2
𝑅2
𝑅1
𝑉𝑖𝑛 +
𝑉
𝑅1 + 𝑅2
𝑅1 + 𝑅2 𝑠
The comparator will switch when 𝑉+ = 0.
R1
Vin must drop below −
V to get output to switch
R2 s
Once the comparator output has switched to
R1
− VS, the threshold becomes
V
R2 s
So this circuit creates a switching band centered around zero,
𝑅
with trigger levels ± 𝑅1 𝑉𝑠
2
𝑅1
𝑉+ =
𝑉
𝑅1 + 𝑅2 𝑠
The comparator will switch when Vin = V+ .
Vin must exceed above this voltage get output to switch
Once the comparator output has switched to
𝑅1
− VS, the threshold becomes
𝑉
𝑅1 + 𝑅2 𝑠
So this circuit creates a switching band centered around zero,
𝑅1
with trigger levels ±
𝑉
𝑅1 + 𝑅2 𝑠
𝑉+ =
Inverting differentiator
1 𝑡
∫ 𝑉 (𝑡) 𝑑𝑡
𝑅𝐶 𝑡0 𝑖𝑛
𝑉𝑜𝑢𝑡 (𝑡) = −𝑅𝐶
𝑑𝑉𝑖𝑛
𝑑𝑡
𝑉𝑜𝑢𝑡 = −
𝑅𝑓
𝑅𝑓
𝑅𝑓
𝑅𝑓
𝑅𝑓
(8𝑉1 + 4𝑉2 + 2𝑉3 + 𝑉4 )
𝑉1 −
𝑉2 −
𝑉3 −
𝑉4 = −
𝑅
2𝑅
4𝑅
8𝑅
8𝑅
𝑉𝑜𝑢𝑡 = 𝐺(2𝑛−1 𝑉1 + 2𝑛−2 𝑉2 + ⋯ + 2𝑉𝑛−1 + 𝑉𝑛 )
𝐺=−
𝑅𝑓
8𝑅
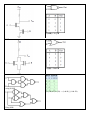
MOSFET
characteristic
ideal
Inverter
NAND
! (A&B) = !A || !B
NOR
! (A||B) = !A & !B
XOR
using NAND
(A || !B) & (!A || B) = (A & B) || (!A & !B)
Using NOR
XNOR
using NAND
(A||B) & (!A || !B)
using NOR
Capacitor
𝑖=𝐶
𝑑𝑣
𝑑𝑡
𝑞 = 𝐶𝑣
𝐶=
𝜀𝐴
𝑑
1 𝑡
∫ 𝑖(𝑡)𝑑𝑡 + 𝑣(𝑡0 )
𝐶 𝑡0
𝑣0
𝐶𝑣0 2
𝐸 = ∫ 𝐶𝑣 𝑑𝑣 =
2
0
𝑉(𝑡) =
𝑑𝑣
+ 𝑎𝑣 = 𝑏
𝑑𝑡
𝑏
𝑣(𝑡) = 𝑣(0)𝑒 −𝑎𝑡 + (1 − 𝑒 −𝑎𝑡 )
𝑎
1
𝑏
𝜏 = 𝑅𝐶 =
= 𝑣(∞)
𝑎
𝑎
𝑡
𝑣(𝑡) = 𝑣(∞)+[𝑣(0) − 𝑣(∞)]𝑒 −𝜏
At DC, capacitor looks like an open circuit
Voltage across a capacitor must be continuous (no
abrupt change)
Inductor
𝑑𝑖
𝑁 2 𝜇𝐴
𝑞 = 𝐶𝑣
𝐿=
𝑑𝑡
𝑙
At DC, inductor looks like a short circuit
Current through an inductor must be continuous (no
abrupt change)
1 𝑡
𝑖(𝑡) = ∫ 𝑣(𝑡)𝑑𝑡 + 𝑖(𝑡0 )
𝐿 𝑡0
𝑣0
𝐿𝑖 2
𝐸 = ∫ 𝐿𝑖 𝑑𝑖 =
2
0
Inductors add together in the same way the resistors
do.
𝑣=𝐿
Phasor
𝑣(𝑡) = 𝑣(∞)+[𝑣(𝑡0 ) − 𝑣(∞)]𝑒 −
𝑡−𝑡0
𝜏
Natural response
𝑉(𝑡) = 𝑉0 𝑒 −𝑡/𝑅𝐶
𝑑𝑖
+ 𝑎𝑖 = 𝑏
𝑑𝑡
𝑡
𝑖(𝑡) = 𝑖(∞)+[𝑖(0) − 𝑖(∞)]𝑒 −𝜏
𝑖(𝑡) = 𝑖(∞)+[𝑖(𝑡0 ) − 𝑖(∞)]𝑒 −
𝐿 1
𝜏= =
𝑅 𝑎
Natural response
𝑖(𝑡) = 𝑖0 𝑒 −𝑅𝑡/𝐿
𝑡−𝑡0
𝜏