Download Lecture 06 Part II a little more history of science

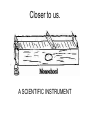
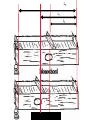
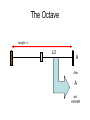
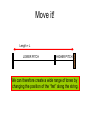
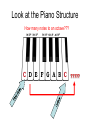
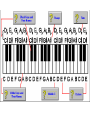
Lecture 06 Part II
a little more history of science
October 1, 2004
From the Anvil flowed an idea (?)
This famous drawing
of Pythagoras
engaged in testing
the relationships of
music and numbers
dates from a 1492
book of Gaffurius:
Theorica Musices,
Milan, 1492.
Pythagoras
Pythagoras Observed …..
• The heavier the bell, the “lower” the tone.
• The water inside a glass was directly
related to the tone.
• He probably NEVER made any of these
observations.
• But he did look at STRINGS and he did
some very interesting “science”.
The Monochord
Closer to us.
A SCIENTIFIC INSTRUMENT
Modern Design
L0
L1
L2
FIRST OBSERVATION
• The shorter the plucked length of the
string, the “higher” the tone.
• With TWO strings, some lengths sounded
well together and some did not.
• Pythagoras studied this carefully and
developed the “mathematics” of the
musical scale.
CLARIFICATION
• The musical scale was NOT invented by
Pythagoras or by anyone else that we
know of.
• But he STUDIED IT.
• The scale was developed naturally based
upon which tones sounded well together.
• The scale probably goes back to the
Neanderthal times (bone flute).
Pythagoras Looked for
“Consonance”
• What length of string will be consonant
with the open string?
• What is consonance??
Consonance
• Two tones are consonant when they sound
pleasing together.
• They are dissonant if they do not.
• BUT whether or not a harmony is pleasing is
a matter of personal taste, as there are
consonant and dissonant harmonies, both of
which are pleasing to the ears of some and
not others.
• Pythagoras did not subscribe to the last
statement.
• Pythagoras tried to define the right string
lengths for harmony.
MOST INPORTANT
L0
L1
• Most harmonious sound (according to
Pythagoras was (L1/L0) = (1/2)
• This is called the OCTAVE
Properties of the Octave
• The two tones almost sound like the same
tone!
– Whatever that means.
• When men and women sing together in
“unison”, they will sing an octave apart and
think they are singing the same tone!
• The octave defines an INTERVAL between
two closely related tones.
Octave
• Having defined the interval of the octave,
we can proceed to put more tones
between them to establish a scale of notes
that may be easily played together.
• Some combinations will not be a
consonant as others but they are still
considered harmonious.
Notation – A practical necessity
HIGH
What about higher?
Notes between
OCTAVE
5
7
pentatonic diatonic
FIRST TONE
LOW What about lower?
A look at the musical scale
~500BC
Length = L
A
Unstopped string produces the primary tone of the scale.
We will start our scale with an A.
The Octave
Length = L
L/2
A
Also
A
but
HIGHER
The octave
• Is a higher pitch
• Sounds higher
• There is “a sameness” about the two
tones when they are played together.
Move it!
Length = L
LOWER PITCH
HIGHER PITCH
We can therefore create a wide range of tones by
changing the position of the “fret” along the string.
Play them together
Length = L
Tone 1
Length = L
Tone 2
Look at the Piano Structure
How many notes to an octave???
?????
Notes & Notation