* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture Set 07
Circle of fifths wikipedia , lookup
Tone cluster wikipedia , lookup
Tone (linguistics) wikipedia , lookup
Chichewa tones wikipedia , lookup
Traditional sub-Saharan African harmony wikipedia , lookup
Consonance and dissonance wikipedia , lookup
Luganda tones wikipedia , lookup
Mode (music) wikipedia , lookup
Interval (music) wikipedia , lookup
Equal temperament wikipedia , lookup
Microtonal music wikipedia , lookup
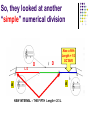
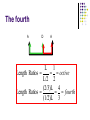
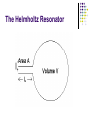
Lecture Set 07 October 4, 2004 The physics of sounds from strings. Things to Note • All lectures are currently posted on the website. – The solution to the exam is also posted on the website. • Some of the files are rather long. – I cut some of the lectures into two or three parts to keel them small but some are still pretty big because of the photographs. – Today, we continue with sounds from strings. Last time • We listened to the sound generated by a single stretched string. • We noted: – The longer the string, the “lower” the tone. – The shorter the string, the “higher” the tone. – The more tension on the string, the “higher” the tone. An Interesting observation • When the string is reduced to half, it produces a tone related to the original tone. • The new tone is said to be an OCTAVE higher than the original. – The textbook calls this interval a “diapason” which in Greek means “through all”. – I am stubborn and will call it an octave anyway. What are we doing? D Half length Open string D’ PLAY THEM TOGETHER AND THEY SOUND REALLY GOOD. What do we have so far?? ‘’D ‘D D D’ D’’ D’’’ D D D D D D L/2 L L/4 L/8 L/4 L/2 So, they looked at another “simple” numerical division D D Also a fifth Length = 1/3 OCTAVE L/3 A A NEW INTERVAL – THE FIFTH Length = 2/3 L Observation The FIFTH sounds good when played with the original tone. Bass and tenors singing together will tend to sing a fifth apart. Recall that men and women, singing the “same tone” together, tend to sing an OCTAVE apart. Our scale now has “two” notes. A little shabby! Differences/Intervals The octave and the fifth represent an interval, or a “difference” between two reasonable consonant tones. Interval is D E F G A B C D E F G A ….= FIFTH New Interval The FOURTH The fourth A D A L 1 Length Ratios octive L/2 2 (2/3)L 4 Length Ratios fourth (1/2)L 3 These “Special” Ratios All of these intervals sounded good to the ear. The lengths corresponding to intervals that sounded good were found to have ratios expressible as small integers. How perfect! God-like! MUST be true. The process can be continued to define additional intervals. The Pythagorean Musical Scale .. Developed by rules The Pythagoreans believed that the laws of physics could be revealed NOT by observation but by pure thought. So they thought about the results that we just mentioned and came up with the “rule” to form the various intervals of the scale. The “RULE” Take an existing ratio (lengths) and multiply or divide it by 3/2. If the number that you get is greater than 2, then halve it. If the number is less than 1, double it. EXAMPLE : 1 x 2/3 produces the fifth. NEXT: 1 x 3/2 = 3/2 .. Divide by 2 … = 3/4 = fourth The rule basically raises or lowers a tone by a fifth and then divides or multiplies by two to keep it in the proper range. So … Then … The Pentatonic Scale The septatonic scale (Our Own but starting with Re instead of Do) By the way … we are cheating! 16th century A 2000 year problem SAME RATIOS!!! The Music of the Spheres The Music of the Spheres Kepler Like Plato and Pythagoras, Kepler believed that the world was ruled by number. He tried hard to prove that the distances of the planets from the sun were given by an arrangement of Eucid's five regular solids; by doing so, he believed, he could demonstrate something of the order of the mind of God. But his faith in number went further: he believed that musical harmony, mathematically expressed, and the harmony of the spheres were one thing: 'I affirm and demonstrate that the movements (of the planets) are modulated according to harmonic proportions’. Let’s talk some physics here. What is observed The string moves back and forth. It sets the air into some kind of motion. The air motion (we presume pressure) strikes the ear and produces what we hear as sound. WE DO NOT YET KNOW THE DIFFERENCE BETWEEN THE VARIOUS TONES OF THE SCALE IN TERMS OF WHAT IT IS THAT TRAVELS THROUGH THE AIR.. Enter Helmholtz ~1885 Air Stream Siren FREQUENCY f number of " events" f second Example Suppose something has a frequency of 60 cycles per second. One cycle per second is defined as the Hertz. So we have 60 hertz. In one second there are 60 events. Therefore ONE event takes 1/60th of a second. That is defined as the PERIOD = T Definition: 1 Period frequency 1 T f fT 1 The Helmholtz Resonator A set of resonators The Epiphany “RESONANCE” TAKES PLACE ONLY WITH THE CORRECT HELMHOLTZ RESONATOR. SOUND HAS A FREQUENCY! BUT HOW DOES IT MOVE TO US?? Waves But What’s Moving??