Download Lecture Set 07

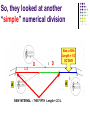
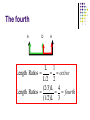
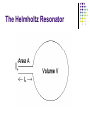
Lecture Set 07
October 4, 2004
The physics of sounds from strings.
Things to Note
• All lectures are currently posted on the
website.
– The solution to the exam is also posted on the
website.
• Some of the files are rather long.
– I cut some of the lectures into two or three
parts to keel them small but some are still
pretty big because of the photographs.
– Today, we continue with sounds from strings.
Last time
• We listened to the sound generated by a
single stretched string.
• We noted:
– The longer the string, the “lower” the tone.
– The shorter the string, the “higher” the tone.
– The more tension on the string, the “higher”
the tone.
An Interesting observation
• When the string is reduced to half, it
produces a tone related to the original
tone.
• The new tone is said to be an OCTAVE
higher than the original.
– The textbook calls this interval a “diapason”
which in Greek means “through all”.
– I am stubborn and will call it an octave
anyway.
What are we doing?
D
Half length
Open string
D’
PLAY THEM TOGETHER AND THEY SOUND REALLY GOOD.
What do we have so far??
‘’D
‘D
D
D’
D’’
D’’’
D
D
D
D
D
D
L/2
L
L/4
L/8
L/4
L/2
So, they looked at another
“simple” numerical division
D
D
Also a fifth
Length = 1/3
OCTAVE
L/3
A
A
NEW INTERVAL – THE FIFTH Length = 2/3 L
Observation




The FIFTH sounds good when played with
the original tone.
Bass and tenors singing together will tend to
sing a fifth apart.
Recall that men and women, singing the
“same tone” together, tend to sing an
OCTAVE apart.
Our scale now has “two” notes. A little
shabby!
Differences/Intervals

The octave and the fifth represent an interval,
or a “difference” between two reasonable
consonant tones.

Interval is D E F G A B C D E F G A ….= FIFTH
New Interval
The FOURTH
The fourth
A
D
A
L
1
Length Ratios 
  octive
L/2 2
(2/3)L 4
Length Ratios 
  fourth
(1/2)L 3
These “Special” Ratios




All of these intervals sounded good to the
ear.
The lengths corresponding to intervals that
sounded good were found to have ratios
expressible as small integers.
How perfect! God-like! MUST be true.
The process can be continued to define
additional intervals.
The Pythagorean Musical
Scale .. Developed by rules


The Pythagoreans believed that the laws of
physics could be revealed NOT by
observation but by pure thought.
So they thought about the results that we just
mentioned and came up with the “rule” to
form the various intervals of the scale.
The “RULE”



Take an existing ratio (lengths) and multiply
or divide it by 3/2.
If the number that you get is greater than 2,
then halve it.
If the number is less than 1, double it.
EXAMPLE : 1 x 2/3 produces the fifth.
NEXT: 1 x 3/2 = 3/2 .. Divide by 2 … = 3/4 = fourth
The rule basically raises or
lowers a tone by a fifth
and then divides or multiplies
by two to keep it in the
proper range.
So …
Then … The Pentatonic Scale
The septatonic scale (Our Own but
starting with Re instead of Do)
By the way … we are cheating!
16th century
A 2000 year problem
SAME RATIOS!!!
The Music of the Spheres
The Music
of the
Spheres
Kepler
Like Plato and Pythagoras, Kepler believed that the
world was ruled by number. He tried hard to prove that
the distances of the planets from the sun were given
by an arrangement of Eucid's five regular solids; by
doing so, he believed, he could demonstrate
something of the order of the mind of God. But his
faith in number went further: he believed that musical
harmony, mathematically expressed, and the harmony
of the spheres were one thing: 'I affirm and
demonstrate that the movements (of the
planets) are modulated according to
harmonic proportions’.
Let’s talk some physics here.
What is observed




The string moves back and forth.
It sets the air into some kind of motion.
The air motion (we presume pressure) strikes
the ear and produces what we hear as
sound.
WE DO NOT YET KNOW THE
DIFFERENCE BETWEEN THE VARIOUS
TONES OF THE SCALE IN TERMS OF
WHAT IT IS THAT TRAVELS THROUGH
THE AIR..
Enter Helmholtz ~1885
Air Stream
Siren
FREQUENCY f
number of " events"
f 
second
Example






Suppose something has a frequency of 60
cycles per second.
One cycle per second is defined as the Hertz.
So we have 60 hertz.
In one second there are 60 events.
Therefore ONE event takes 1/60th of a
second.
That is defined as the PERIOD = T
Definition:
1
Period 
frequency
1
T
f
fT  1
The Helmholtz Resonator
A set of resonators
The Epiphany
“RESONANCE” TAKES PLACE ONLY
WITH THE CORRECT HELMHOLTZ
RESONATOR.
SOUND HAS A FREQUENCY!
BUT HOW DOES IT MOVE TO US??
Waves
But What’s Moving??