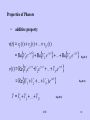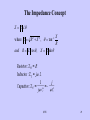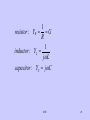Download Chapter 9 Sinusoids and Phasors

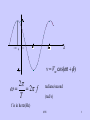
Chapter 9
Sinusoids and Phasors
SJTU
1
Sinusoids
A sinusoid is a signal that has the form of the sine or
cosine function.
v  Vm cos(t   )
where Vm  amplitude
  angular frequency
t    arg ument
  phase angle
SJTU
2
t


v  Vm cos(t   )
2

 2 f
T
radians/second
(rad/s)
f is in hertz(Hz)
SJTU
3
v1 (t )  Vm1 cos( t  1 )
v2 (t )  Vm 2 cos( t  2 )
Phase difference:
  ( t  1 )  ( t   2 )
 1   2
if   0 v1 and v 2 are out of phase
  0 v1 and v 2 are in phase
  0 v1 leads v 2 by 
  0 v1 lags v 2 by 
SJTU
4
Complex Number
z  x  jy rectangula r form
z  r polar form
z  rcos  jrsin sinusoidal form
z  re j
exponentia l form

SJTU
5
Phasor
a phasor is a complex number representing the amplitude
and phase angle of a sinusoidal voltage or current.
Eq.(8-1)
Eq. (8-2)
and
Eq.(8-3)
SJTU
6
When Eq.(8-2) is applied to the general sinusoid we obtain
Eq.(8-4)
The phasor V is written as
Eq.(8-5)
SJTU
7
Fig. 8-1 shows a graphical representation commonly called
a phasor diagram.
Two features of the phasor concept
need emphasis:
1. Phasors are written in boldface
type like V or I1 to distinguish
them from signal waveforms
such as v(t) and i1(t).
Fig. 8-1: Phasor diagram
2. A phasor is determined by
amplitude and phase angle and
does not contain any
information about the frequency
of the sinusoid.
SJTU
8
In summary, given a sinusoidal signal
, the
corresponding phasor representation is
. Conversely,
given the phasor
, the corresponding sinusoid is found
by multiplying the phasor by
and reversing the steps in
Eq.(8-4) as follows:
Eq.(8-6)
v(t )  Vm cos(t   )
V  Vm
Phase-domain
representation
Time domain
representation
SJTU
9
Properties of Phasors
•
additive property
Eq.(8-7)
Eq.(8-8)
Eq.(8-9)
SJTU
10
• derivative property
Eq.(8-10)
dv

 jV
dt
Time domain
representation
Phase-domain
representation
SJTU
11
• Integral property
V
 vdt  j
Time domain
representation
Phase-domain
representation
The differences between v(t) and V:
1. V(t) is the instantaneous or time-domain representation,
while V is the frequency or phasor-domain
representation.
2. V(t) is a real signal which is time dependent, while V is
just a supposed value to simplify the analysis
SJTU
12
The complex exponential is sometimes called a rotating phasor,
and the phasor V is viewed as a snapshot of the situation at t=0.
Fig. 8-2: Complex exponential
SJTU
13
v  Vm cos2  f  t   10 cos2  0.5  t 
+ j  = 90 or  /2
In this particular case
10V rms ac signal at 0.5 Hz
14.142 15
12
9
t
 = 180 or 
=0
+
real
- real
Voltage in volts
6
Vm
v imag  t n
3
0
3
6
9
12
 14.142
15
angular frequency times time in radians
- j  = -90 or - /2
0
10V rms ac signal at 0.5 Hz
0
5
10
15
0
(  t) n
12.566
angular frequency times time in radians
The proj ectionof the rotating
phasor on the j (im aginary) axis is
v im a g  V m  sin(t )
0
1.5
3
4.5
  t n
6
7.5
The proj ectionof the rotating
phasor on the realaxis is
vrea l  Vm  cos(t )
9
10. 5
12
 12. 56613. 5
15
15
 14. 142
10
5
0
5
v real( t) n
voltage in volts
10
15
14. 142
SJTU
14
EXAMPLE 8-1
(a) Construct the phasors for the following signals:
(b) Use the additive property of phasors and the phasors
found in (a) to find v(t)=v1(t)+v2(t).
SOLUTION
(a) The phasor representations of v(t)=v1(t)+ v2(t) are
SJTU
15
(b) The two sinusoids have the same frequent so the additive
property of phasors can be used to obtain their sum:
The waveform corresponding to this phasor sum is
j
V2
1
V
V1
SJTU
16
EXAMPLE 8-2
(a) Construct the phasors representing the following signals:
(b) Use the additive property of phasors and the phasors found
in (a) to find the sum of these waveforms.
SOLUTION:
(a) The phasor representation of the three sinusoidal currents are
SJTU
17
(b) The currents have the same frequency, so the additive
property of phasors applies. The phasor representing the sum of
these current is
Fig. 8-4
SJTU
18
EXAMPLE 8-3
Use the derivative property of phasors to find the time derivative
of v(t)=15 cos(200t-30° ).
SOLUTION:
The phasor for the sinusoid is V=15∠-30 ° . According to
the derivative property, the phasor representing the dv/dt is
found by multiplying V by j .
The sinusoid corresponding to the phasor jV is
SJTU
19
Device Constraints in Phasor Form
Resistor:
jIm
V
I
0
Re
Vm  I m R
Voltage-current relations for a resistor in the: (a) time
domain, (b) frequency domain.
SJTU
V   I
20
Device Constraints in Phasor Form
Inductor:

Vm  LI m
V   I  90
Voltage-current relations for an inductor in the: (a) time
domain, (b) frequency domain.
SJTU
21
Device Constraints in Phasor Form
Capacitor:

Voltage-current relations for a capacitor in the:
(a) time domain, (b) frequency domain.
SJTU
I m  CVm
 I  V  90
22
Connection Constraints in Phasor Form
KVL in time domain
Kirchhoff's laws in phasor form (in frequency domain)
KVL: The algebraic sum of phasor voltages around a loop is
zero.
KCL: The algebraic sum of phasor currents at a node is zero.
SJTU
23
The Impedance Concept
The IV constraints are all of the form
V=ZI
or
Z= V/I
Eq.(8-16)
where Z is called the impedance of the element
The impedance Z of a circuit is the ratio of the phasor voltage
V to the phasor current I, measured in ohms()
Z  R  jX
where R  Re Z is the resistance and X  Im Z is the reactance.
The impedance is inductive when X is positive
is capacitive when X is negative
SJTU
24
The Impedance Concept
Z  Z 
where Z  R 2  X 2 ,   tan 1
and
R  Z cos ,
X
R
X  Z sin 
SJTU
25
EXAMPLE 8-5
Fig. 8-5
The circuit in Fig. 8-5 is operating in the sinusoidal steady state
with
and
. Find the impedance of
the elements in the rectangular box.
SOLUTION:
SJTU
26
I 3  V2 /RL  0.278  37.9
SJTU
27
The Admittance Concept
The admittance Y is the reciprocal of impedance,
measured in siemens (S)
1 I
Y 
Z V
Y=G+jB
Where G=Re Y is called conductance and B=Im Y is called
the susceptance
How get Y=G+jB from
Z=R+jX ?
G  jB 
G
SJTU
1
R  jX
R
X
,
B


R2  X 2
R2  X 2
28
1
resistor : YR   G
R
1
inductor : YL 
jL
capacitor : YC  jC
SJTU
29
Basic Circuit Analysis with Phasors
Step 1: The circuit is transformed into
the phasor domain by representing the
input and response sinusoids as phasor
and the passive circuit elements by
their impedances.
Step 2: Standard algebraic circuit
techniques are applied to solve the
phasor domain circuit for the desired
unknown phasor responses.
Step 3: The phasor responses are
inverse transformed back into timedomain sinusoids to obtain the
response waveforms.
SJTU
30
Series Equivalence And Voltage Division
where R is the real part and X is the imaginary part
SJTU
31
EXAMPLE 8-6
Fig. 8-8
The circuit in Fig. 8 - 8 is operating in the sinusoidal steady
state with
(a) Transform the circuit into the phasor domain.
(b) Solve for the phasor current I.
(c) Solve for the phasor voltage across each element.
(d) Construct the waveforms corresponding to the phasors found
in (b) and (c)
SJTU
32
SOLUTION:
SJTU
33
PARALLEL EQUIVALENCE AND
CURRENT DIVISION
I
Rest of
the
circuit
V
Y1
Y
1
I1
Y2
I2
YN
I3
phasor version of the current division principle
SJTU
34
EXAMPLE 8-9
Fig. 8-13
The circuit in Fig. 8-13 is operating in the sinusoidal
steady state with iS(t)=50cos2000t mA.
(a) Transform the circuit into the phasor domain.
(b) Solve for the phasor voltage V.
(c) Solve for the phasor current through each element.
(d) Construct the waveforms corresponding to the phasors
found in (b) and (c).
SJTU
35
SOLUTION:
(a) The phasor representing the input source current is
Is=0.05∠0°A. The impedances of the three passive elements
are
Fig. 8-14
SJTU
36
And the voltage across the parallel circuit is
The current through each parallel branch is
The sinusoidal steady-state waveforms corresponding to the
phasors in (b) and (c) are
SJTU
37
EXAMPLE 8-10
Fig. 8-15
Find the steady-state currents i(t), and iC(t) in the circuit of
Fig. 8-15 (for Vs=100cos2000t V, L=250mH, C=0.5  F, and
R=3k ).
SOLUTION:
Vs=100∠0°
SJTU
38
SJTU
39
SJTU
40
Y←→△ TRANSFORMATIONS
The equations for the △ to Y
transformation are
SJTU
41
The equations for a Y-to- △ transformation are
when Z1=Z2=Z3=ZY or ZA=ZB=ZC=ZN.
ZY=ZN /3 and ZN =3ZY
SJTU
balanced conditions
42
EXAMPLE 8-12
Use a △ to Y transformation to solve for the phasor current IX
in Fig. 8-18.
SOLUTION:
ABC △ to Y
Fig. 8-18
SJTU
43
SJTU
44