* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Math 1B – Solving Radicals
Kerr metric wikipedia , lookup
Two-body Dirac equations wikipedia , lookup
Unification (computer science) wikipedia , lookup
BKL singularity wikipedia , lookup
Two-body problem in general relativity wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Debye–Hückel equation wikipedia , lookup
Schrödinger equation wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Perturbation theory wikipedia , lookup
Equations of motion wikipedia , lookup
Dirac equation wikipedia , lookup
Euler equations (fluid dynamics) wikipedia , lookup
Van der Waals equation wikipedia , lookup
Calculus of variations wikipedia , lookup
Differential equation wikipedia , lookup
Heat equation wikipedia , lookup
Partial differential equation wikipedia , lookup
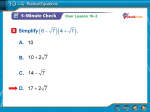
Notes on Solving Radical Equations Name_________________________ An equation that has a radical with a variable under the radicand is called a radical equation. The radicand is the numbers and variables under the symbol. That is the number that we are taking the square root of. For example, the radicand in 3x is 3x. Steps for Solving Radical Equations 1. Isolate the radical. 2. Square BOTH sides. The most common mistake is students only square one side. 3. Isolate the variable. 4. Check your answer – it is possible that your answer will not work (no solution). Example 1 x 20 2 x 20 20 2 20 Add twenty to both sides of the equation. x 22 x 22 2 2 Square both sides of Check your answer by substituting it back into the original equation. 484 20 2 the equation. 22 20 2 x 484 The solution is x = 484. 22 This is a true equation, so the answer must be correct. -----------------------------------------------------------------------------------------------------------------------------Example 2 x 52 x 3 Subtract 5 from each side. Wait!! You cannot have Let’s continue with the problem to see what will happen. x 3 2 2 The solution is x = 9. Now we need to check the solution. 9 52 3 5 2 8 2 . Since eight is not equal to 2 we know that -3 is not a solution to the equation x 5 2 . x cannot equal a negative number. x 9 x equal to -3. The Squaring both sides of the equation a = b can result in a solution of a 2 b 2 that is not a solution of the original equation. Such a solution is called an extraneous solution. ----------------------------------------------------------------------------------------------------------------------------- Example 3 3 x 6 10 14 3 x 6 10 10 14 10 3 x 6 24 3 x 6 24 3 3 Add ten to both sides of the equation. Divide each side by 3. x6 8 x 6 8 2 2 Square both sides of Now, check your answer by substituting it back into the original equation. the equation. x 6 64 x 6 6 64 6 Subtract 6 from both sides. x 58 The solution is x =58. -----------------------------------------------------------------------------------------------------------------------------Now you try: 2 x 4 3 15 . Check your answers. -----------------------------------------------------------------------------------------------------------------------------Example 4 11 3x 2 11 2 3x 2 2 Square both sides of the equation. 121 3x 2 121 2 3x 2 2 Add 2 to both sides. 123 3x Divide each side by 3. x 41 The solution is x=41. Now, check your answer by substituting it back into the original equation. Homework on Solving Radical Equations Name_________________________ Solve for x. 1.) 4 2x 3 12 2.) 2 9x 1 20 10 3.) 8 x 32 0 x 3 8 15 6.) 8 3x 5 6 5.) x 6 2 4 7.) 3 x 5 3 6 8.) 2 9x 1 20 9.) 4.) 2x 15 3 10.) 15 2x 2 13