Download Math 1B – Solving Radicals

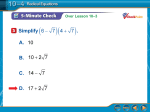
Notes on Solving Radical Equations
Name_________________________
An equation that has a radical with a variable under the radicand is called a radical equation. The
radicand is the numbers and variables under the
symbol. That is the number that we are taking the
square root of. For example, the radicand in 3x is 3x.
Steps for Solving Radical Equations
1.
Isolate the radical.


2.
Square BOTH sides. The most common mistake is students only square one side.
3.
Isolate the variable.
4.
Check your answer – it is possible that your answer will not work (no solution).
Example 1
x  20  2
x  20  20  2  20


Add twenty to both sides of the equation.
x  22
 x   22
2
2
Square both sides of


Check your answer by substituting it back
into the original equation.
484  20  2
the equation.
22  20  2
x  484
The solution is x = 484.


22

This is a true equation, so the answer must be
correct.

-----------------------------------------------------------------------------------------------------------------------------Example 2
x 52
x  3
Subtract 5 from each side.

Wait!! You cannot have

Let’s continue with the problem to see what will happen.
 x   3
2
2


The solution is x = 9.
Now we need to check the solution.
9 52
3 5  2
8  2 . Since eight is not equal to 2 we know that -3 is not a solution to the
equation x  5  2 .


x cannot equal a negative number.

x 9

x equal to -3. The

Squaring both sides of the equation a = b can result in a solution of a 2  b 2 that is not a solution of the
original equation. Such a solution is called an extraneous solution.
-----------------------------------------------------------------------------------------------------------------------------
Example 3
3 x  6 10 14
3 x  6 10 10 14 10

3 x  6  24

3 x  6 24

3
3

Add ten to both sides of the equation.
Divide each side by 3.
x6 8

 x  6   8
2
2
Square both sides of





Now, check your answer by
substituting it back into the original
equation.
the equation.
x  6  64
x  6  6  64  6
Subtract 6 from
both sides.
x  58
The solution is x =58.
-----------------------------------------------------------------------------------------------------------------------------Now you try: 2 x  4  3 15 . Check your answers.

-----------------------------------------------------------------------------------------------------------------------------Example 4
11  3x  2
11
2


 3x  2 
2
Square both sides of the equation.
121  3x  2

121 2  3x  2  2
Add 2 to both sides.

123  3x
Divide each side by 3.

x  41
The solution is x=41.


Now, check your answer by
substituting it back into the original
equation.
Homework on Solving Radical Equations
Name_________________________
Solve for x.
1.) 4 2x  3 12

2.) 2 9x 1  20 10

3.) 8 x  32  0

x  3  8 15
6.)
8  3x  5  6

5.)
x 6 2  4


7.) 3 x  5  3  6

8.) 2 9x 1  20

9.)

4.)
2x 15  3
10.) 15  2x  2 13
