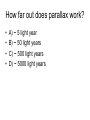* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Goal: To understand how we know distances to
International Ultraviolet Explorer wikipedia , lookup
Hubble Deep Field wikipedia , lookup
Geocentric model wikipedia , lookup
Perseus (constellation) wikipedia , lookup
History of supernova observation wikipedia , lookup
Extraterrestrial skies wikipedia , lookup
Hubble's law wikipedia , lookup
Star formation wikipedia , lookup
Aquarius (constellation) wikipedia , lookup
Type II supernova wikipedia , lookup
Future of an expanding universe wikipedia , lookup
Observable universe wikipedia , lookup
Corvus (constellation) wikipedia , lookup
Observational astronomy wikipedia , lookup
Dialogue Concerning the Two Chief World Systems wikipedia , lookup
Timeline of astronomy wikipedia , lookup
Goal: To understand how we know distances to various objects (the distance scale) 2) 3) 4) 5) Objectives: 1) To learn about Radar (the sun) To learn about Parallax (nearby stars) To learn about using Cepheid variables (galaxy and nearby galaxies) To understand the Hubble relationship To understand how to use Supernovae (all the way across the universe) How do we know the closest distance to us, the sun? • Not as easy of a question as you think. • Imagine you were sent back in time and you had to explain that the earth is an average of 93 million miles from the sun – how would you do that? Here is what you say • Um, you can’t prove it… • All you could do is give the ratio’s of the distances (i.e. you could prove using orbits that Jupiter was 5.2 AU from the sun – whatever the AU actually was). Radar! • 50 years ago we finally COULD measure the distance to the sun! • We used radar. • No, we didn’t send the radar to the sun. • What we did was send radar to Venus, and wait for the reflected beams to return. • This would take several minutes, but could be done. • Since we knew the speed of light we could therefore find the distance to Venus. The AU • Since we knew that the earth was 1 AU away, and we could know what the distance for Venus was for the sun in AU, if we knew the distance from Venus to Earth then we knew the distance from Venus to the sun, and the distance from the sun to Earth. • Radar is good out to 50 AU (4.6 billion miles). 2nd rung - parallax • The first use of parallax was done by Tycho Brahe 500 years ago. • He discovered that on the same night in 2 different locations on the earth that the moon had a slightly different position with respect to the stars. • This allowed Tycho to find the distance to the moon! • But how does this work? What is parallax? • Hold out your thumb as far as possible and close 1 eye. • Then at the same time open the closed eye and close the opened eye. • Your thumb will appear to move compared to stuff further away. • The angle the thumb moves depends on the distance between your eyes divided by the distance your thumb is away from your eye. • The larger the apparent movement, the shorter the distance (and vica versa). • Half the movement means twice the distance away. Astronomical parallax • When we talk about “parallax” what are we usually referring to? • A) the apparent difference in position with respect to further objects for 2 positions on the surface of the earth • B) the apparent difference in position of a star over the course of a year • C) the apparent difference in the position of a star over the course of 6 months • D) how quickly the star appears to move across our sky Using our orbit around the sun! • If we pick 2 places 6 months apart we are on opposite sides of the sun. • We move a distance of 2 AU. • So, if we look 90 degrees away from the sun at both points, we will see a slightly different angle with respect to stars even further away If an object has a parallax motion of 1 arcsecond how far away from the earth is it? • • • • A) 1 light year B) 1 AU C) 1 parsec D) 1 trillion miles Parallax distance • Distance = 1 parsec / parallax motion in arcseconds How far out does parallax work? • • • • A) ~ 5 light year B) ~ 50 light years C) ~ 500 light years D) ~ 5000 light years Best in show! • The Hipparcos satellite was able to take the most accurate images ever. • Therefore it was able to spot parallax movement from a few hundred parsec. • Past that the movements are too small to be detected – yet. Secondary Calibrators • These are calibrators that depend on the “primary” ones (radar + parallax). • If there is a change to the primary one, then all the secondary ones change too. • What do you think the first secondary calibrator is? Apparent vs. absolute magnitudes • If you compare the apparent and absolute magnitudes of an object you get its distance. • How to do that? • 1) spectra – tells you what the mass of the star is by its temperature and its spectral type (although does not work so well for giants – works great for main sequences stars, but this separates them. • 2) Main sequence fitting of clusters – we have done this one already • This is good for about a few million light years (we are getting better at some of this). Variable stars • The other secondary is variable stars. • The most common is Cepheid variables (because they are the brightest). • As has been mentioned before, the period of the variable depends on the size. • So, if you know the period, you know the size. • If you know the size and temperature then you know how bright it actually is. • If you know its actual brightness and its apparent brightness you know its distance! Tertiary Calibrators • These are calibrators that depend on the secondary (which depend on the primary). • These have bigger error bars than the primary and secondary. • Therefore these calibrators are constantly been improved and updated. • All of these try to relate the brightness of a galaxy to some other value. Tully Fisher • The first is the Tully Fisher relationship. • This compares the rotation of the galaxy to the brightness (the rotation gives an indication of mass which therefore would affect brightness). • The rotation is found using the Doppler shifts of the 21 cm line of Hydrogen. • You can also use bright objects such as very massive stars, novae, and some supernova. • There is also some who think the size of a black hole in the core of the star might also determine brightness (or even the brightness of the bulge). • Overall this works somewhat for galaxies out to 150 Mpc (500 million light years) Galaxy size and apparent brightness • If you make the assumption that all galaxies are the same size then you can crudely (within about a factor of a few) estimate the size and distance to a spiral galaxy using either its apparent brightness (and comparing to the absolute brightness of the average spiral galaxy) or its apparent angular size (smaller means further away as all are about 100,000 light years across). Standard Candles • Now we are starting to get across the universe! • Supernovae are so bright that they can be seen across the ENTIRE UNIVERSE! • However, can we tell the absolute brightness of a supernova? • To do that, they have to be the same, or have some pattern or relation. Type Ia • Type Ia supernovae (which occur when white dwarfs get too much mass by either taking it from a companion, or more usually spiral into another white dwarf) are all the same brightness because they all do the same thing. • So, we can judge the distance by the apparent brightness of the explosion. Type II supernovae • Type II (Type II just means that there is some Hydrogen in the supernova. Type Is have none) supernovae come from massive stars. • However, each star is a different mass, and therefore a different brightness of supernova. • The trick is that the bigger stars are brighter, and have longer peaks. • This one is not very accurate, but gives some idea to distances. Hubble’s law • It turns out that our universe is expanding. • So, almost everything (with the exceptions of the most nearby galaxies like Andromeda) is moving away from us. • Quite simply, the velocity an object moves away from us is just proportional to distance (twice the distance means twice the speed). • V = Ho * d (Ho is called Hubble’s constant) • So, if you measure the velocity away from us (once again we use the Doppler shift) then we know the distance. Redshift • This velocity causes what we call Cosmological redshift. • This redshift tells us the distance to the galaxy – sort of. • However, guess what, that galaxy is moving away from us. • So, does the distance we get tell us the distance it is NOW or the distance it was THEN, or maybe halfway between? • So, really, what we have is not a “distance” but a look back time. complications • There are a few more complications. • First, our planet, star, and galaxy are all in motion (but we can account for that as we will find out how later). • The rate of expansion is not 100% known. We think we know it to 10%, but there seem to be 2 groups who differ by 25-50% and each claim to know it to 10%. • As we will see later that brings up a big dilemma. • Also, the rate of expansion does NOT seem to be constant with time (cosmological constant). • So, this is only fairly accurate to about 2 billion light years. Conclusion • We estimate distances using a wide range of methods. • Many of these methods are calibrated using the previous methods. • By doing this we can created a ladder of methods which go from our sun to the far edges of the observable galaxy. • However, if you make any changes or adjustments to one you change all of the methods which depend on that. • With time we have better telescopes and better ways to use them and our methods continue to improve (translation we can measure distances farther out with lower error bars).