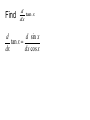Download 3.5 Derivatives of Trigonometric Functions

3.5 Derivatives of
Trigonometric Functions
What you’ll learn about….
•Derivatives of the Sine and Cosine Functions
•Simple Harmonic Motion
•Jerk
•Derivatives of the Tangent, Cotangent, Secant
and Cosecant functions
Warm Up: Exploration 1
Page 141
Graph sin x and nderiv(sin (x), x, x) in a
trigonometric window
Make a conjecture, what function do you
believe is the derivative of sin x?
If f(x) = sin x, then f’(x) =
Derivatives of Trigonometric Functions
d
sin x  cos x
dx
d
csc x   csc x cot x
dx
d
cos x   sin x
dx
d
sec x  sec x tan x
dx
d
tan x  sec 2 x
dx
d
2
cot x   csc x
dx
Find
d
tan x
dx
d
d sin x
tan x 
dx
dx cos x
Example 1:
Use the product & quotient rules to find the following derivatives
d 2
x cos x
dx
d sin x
dx 1  cos x
Simple Harmonic Motion
The motion of a weight bobbing up and down on the end of a spring is an
example of simple harmonic motion. If a weight hanging from a spring is
stretched 5 units beyond its resting position (s=0) and released at time t = 0
to bob up and down, its position at any later time t is
s = 5 cos t.
What is its velocity and acceleration at time t?
v(t) =
a(t) =
Describe its motion.
Starts at
Greatest Velocity
Amplitude
Period
Greatest Acceleration
What about JERK?
A sudden change in acceleration is called a “jerk”. The
derivative responsible for jerk is the third derivative of
position.
Jerk is the derivative of acceleration. If a body’s position at
time t is s(t), the body’s jerk at time t is
3
da d s
j (t ) 
3
dt dt
Example 3: A Couple of Jerks
a)
FYI The jerk caused by the constant acceleration of
gravity (g = -32 ft/sec2) is zero.
This explains why we don’t experience motion sickness sitting
around!
b)
Find the jerk of the simple harmonic motion in Example 2.
Finding Tangent and Normal Lines
Find equations for the lines that are tangent and normal to
sin x
the graph of f ( x) 
x
Slope of tangent
Tangent line
Normal line
Example 5 A Trigonometric Second Derivative
Find y” if y = csc x.
Find more examples & Practice
http://archives.math.utk.edu/visual.calculus/index.html
Select Derivatives
Derivatives of the Trigonometric Functions
Tutorial
Drill with Power Rule
Drill with Quotient Rule
Homework
Page 146
Quick Review 1-10
Exercises 1-11 odds
Agenda for Today
Opener
Page 155 Exercises 70-73
No Calculator! (turn in when completed)
Present homework under document camera
Class / Homework
Page 146
Exercises 13-31 odds, 37, 40, 42