* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download prime numbers, complex functions, energy levels and Riemann.
Survey
Document related concepts
Transcript
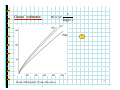
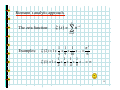
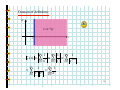
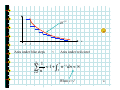
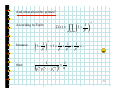
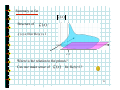
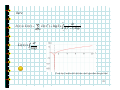
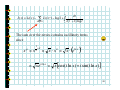
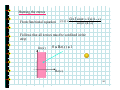
Subtle relations: prime numbers, complex functions, energy levels and Riemann. Prof. Henrik J. Jensen, Department of Mathematics, Imperial College London. At least since the old Greeks mathematics the nature of the prime numbers has puzzled people. To understand how the primes are distributed Gauss studied the number (x) of primes less than a given number x. Gauss fund empirically that (x) is approximately given by x/log(x). In 1859 Riemann published a short paper where he established an exact expression for (x). However, this expression involves a sum over the zeroes of a certain complex function. The properties of the zeroes out in the complex plane determine the properties of the primes! Riemann conjectured that all the relevant zeroes have real part . This has become known as the Riemann hypothesis and is considered to be one of the most important unsolved problems in mathematics. Some statistical properties of the zeroes are known. Surprisingly it has become clear that the zeroes are distributed according to the same probability function that describes the energy levels of big atomic nucleuses. Hence we arrive at a connection between the prime numbers and quantum energy levels in nuclear physics. 1 Subtle relations: Prime numbers, Complex functions, Energy levels and Riemann Henrik Jeldtoft Jensen, Dept of Mathematics Background from: http://www.math.ucsb.edu/~stopple/zeta.html 2 Even numbers: 2, 4, 6, 8 , … Odd numbers: 1, 3, 5, 7, … The primes: 2, 3, 5, 7, 11, 13, … what’s the pattern? Complex numbers s=x+iy = ei Energy levels of heavy nucleuses Dyson Zeroes of (s) Quantum mechanics of chaotic systems Riemann Hugh L Montgomery 3 Odlyzko Motto of the talk: Why it is a good idea to know about complex numbers and complex functions. Copied from http://www.union.ic.ac.uk/dsc/physoc/index.php 4 Content: 1. Number of primes less than x 2. Riemann’s 1859 paper 3. Analytic continuation 4. Energy levels of large nucleuses 5. Random matrix theory 6. The same statistics 5 Number theory: (x) = number of primes less than x 8 6 4 2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 6 Gauss’ estimate: x ( x) log( x ) From J Derbyshire: Prime Obsession 7 Riemann’s analytic approach. The zeta function: ( s) = n s n =1 Examples: 2 1 1 1 ( 2) = 1 + + + + ... = 4 9 16 6 1 1 1 1 (1) = 1 + + + + + ... = 2 3 4 5 8 Domain of definition: iy s=x+iy x 1 1 1 1 ( s ) = s s = x +iy n =1 n n =1 n n =1 n = n =1 1 1 = x x iy n n n =1 n 9 n x n 1 2 Area under blue steps < Area under red curve 1 x < 1 + n dn < x 2 n =1 n When x>1 10 And what about the primes? 1 ( s ) = 1 s p p prime According to Euler: 1 1 because: then: 1 1 1 1 1 s = 1 + s + 2 s + 3s + ... p p p p 1 (p m1 1 m2 2 p Lp ) mq s q 1 = s n 11 From Euler’s product we learn: 1. Prime numbers are hidden inside 2. And (s ) ( s ) 0 when product formula valid Since 1 1 1 1 0 = 1 s p such that 1 - s = 0 p p p Not possible 12 Summary so far (s ) Structure of (s ) : ( s ) 0 for Re( s ) > 1 s=1 Where is the relation to the primes? Can one make sense of (s ) for Re(s)<1? 13 We start with the Re(s) <1 issue. To illustrate the nature of what Riemann did consider the function: 1 1 - z for z < 1 2 3 f ( z) = 1 + z + z + z + L = for z < 1 Cannot be used for |z|>1 Well defined for all z 1 The extension beyond |z|<1 is UNIQUE! 14 Riemann’s extension of (z ) Im(s ) (1 s ) u s 1 du ( s) = u 2i P e 1 Re(s ) P Valid for all z1 Where (z ) is the Gamma function originating from the usual n! = n ( n 1)( n 2) L 2 1 15 The functional equation for the zeta function ( 2 ) sin( s / 2) (1 s ) ( s) = s sin( s ) ( s ) From this follows that ( s ) = 0 for s = 2,4,6,K and that all other zeroes MUST lie in the strip 0 Re( s ) 1 the critical strip 16 Why is it interesting? Because the primes can be found from the zeroes of (s). Consider 0 for x = 0 jump by 1 when x = prime p J ( x ) = jump by 1 when x = prime squares p 2 2 1 when x = prime cubes p 3 jump by 3 ect. J(x) Defined to be “halfway” at jumps 1 2 x 17 Express (x) in terms of J(x) express J(x) in terms of Li(x) evaluated at the complex zeroes of (x) Procedure: complex zeroes of (x) J(x) (x) & Li(x) 18 Riemann’s hypothesis All complex zeroes are confined to 1 Re( s ) = 2 With 30 ( s) = n s 20 n =1 continued to 10 -2 1 (1 s ) u s 1 du ( s) = u 2i P e 1 19 Why is it interesting? Because the primes can be found from the zeroes of (s). According to Riemann: M μ (n) J ( x1 / n ), ( x) = n n =1 with μ = 1,0,1 and M = log x log 2 and dt J ( x ) = Li ( x ) Li ( x ) log 2 + 2 t (t 1) log t Im >0 x 20 here dt J ( x ) = Li ( x ) Li ( x ) log 2 + 2 t (t 1) log t Im >0 x x dt log t 0 Li ( x ) = From:http://mathworld.wolfram.com/LogarithmicIntegral.html 21 dt J ( x ) = Li ( x ) Li ( x ) log 2 + 2 t (t 1) log t Im >0 x The sum over the zeroes contains oscillatory terms since x =x 1 +it 2 = xe = x x = x (e it it ln x ) ln x it = x [cos(t ln x ) + i sin(t ln x )] 22 Adding up the contribution from the zeroes From (http://www.maths.ex.ac.uk/~mwatkins/zeta/encoding2.htm) (x) Some zeroes included x No zeroes included 23 Hunting the zeroes From functional equation s ( 2 ) sin( s / 2) (1 s ) ( s) = sin( s ) ( s ) Follows that all zeroes must be confined in the strip 0 Re( s ) 1 Im(s ) 1 Re(s ) 24 Riemann conjectured in 1859 that zeroes are all on the line 1 Re( s ) = 2 But he couldn’t prove it! Im(s ) 1 Re(s ) Nor has anyone else been able to ever since. Now it is the Riemann Hypothesis. Prove it and get 106 $ from the Clay Institute. 25 Numerical results support the Riemann Hypothesis: • Andrew M. Odlyzko The 1020-th zero of the Riemann zeta function and 175 million of its neighbours • Sebastian Wedeniwski The first 1011 nontrivial zeros of the Riemann zeta function lie on the line Re(s) = 1/2 . Thus, the Riemann Hypothesis is true at least for all |Im(s)| < 29, 538, 618,432.236 which required 1.3 . 1018 floating-point operations 26 A zero off the critical line would induce a pattern in the distribution of the primes: J ( x ) = Li ( x ) Im >0 dt 2 t ( t 1) log t x Li ( x ) log 2 + x Re( s ) [cos(t ln x ) + i sin(t ln x )] Zeroes with different Re(s) would contribute with different weights 27 The distribution along the critical line determines the distribution of the primes. So how are they distributed? Hugh L Montgomery’s Pair Correlation Conjecture: Derived from the Riemann Hypothesis plus conjectures concerning twin primes. Spacing between zeroes controlled by sin u 1 u 2 28 Dyson spotted that the same function describes the spacing between energy levels, i.e., eigenvalues of Hamiltonians describing big nucleuses: Im(s) E Statistically equivalent? Re(s) Random matrices (Gaussian unitary ensemble) 1/2 The imaginary zeroes of (s) 29 Connection between random matrices and (s) confirmed numerically: From: J. Brian Conrey, Notices of the AMS, March 2003, p. 341 30 Puzzle: However as one study the correlations between the Nth and the Nth+K zeroes for large N and K the statistics doesn’t exactly fit the GUE. M. Berry pointed out that the correlations between the zeroes of (s) are like the correlations of the energy levels of a Quantum Chaotic system. 31 Conclusion • Complex analysis is impressively powerful •Profoundly surprising connections: primes, energy levels, quantum chaos Background from: http://www.math.ucsb.edu/~stopple/zeta.html 32 Some references: Technical: H.M. Edwards: Riemann’s Zeta Function M.L. Mehta: Random Matrices Non-technical: J. Derbyshire: Prime Obsession M. du Sautoy: The Music of the Primes A very useful link that contains a wealth of references: Matthew R. Watkins' home page namely: http://www.maths.ex.ac.uk/~mwatkins/ 33 What to see the slides again? Can be found at: www.ma.imperial.ac.uk/~hjjens 34