To test whether a fraction is in lowest terms, you need to know the
... number have to have 1 above the square root and one below the square root so once you get to the square root you should have gotten one. Ex. The square root of 225 is 15. I can write 225 as a ...
... number have to have 1 above the square root and one below the square root so once you get to the square root you should have gotten one. Ex. The square root of 225 is 15. I can write 225 as a ...
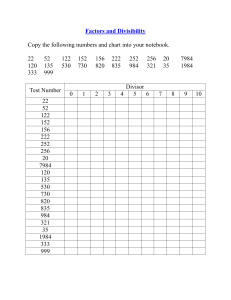
Characteristic of number Number divisible by
... 3 If the sum of the digits is divisible by 3, the number is also. 4 If the last two digits form a number divisible by 4, the number is also. 5 If the last digit is a 5 or a 0, the number is divisible by 5. 6 If the number is divisible by both 3 and 2, it is also divisible by 6. 7 Take the last digit ...
... 3 If the sum of the digits is divisible by 3, the number is also. 4 If the last two digits form a number divisible by 4, the number is also. 5 If the last digit is a 5 or a 0, the number is divisible by 5. 6 If the number is divisible by both 3 and 2, it is also divisible by 6. 7 Take the last digit ...
Divisibility Rules - hrsbstaff.ednet.ns.ca
... could tell if something was divisible by a number just by looking at it? These rules are how they do it. Memorize a few simple rules and simplifying fractions and prime factorization will be so much easier. Number Divisibility Rule Example Two (2) A number is divisible by two if it is even. Another ...
... could tell if something was divisible by a number just by looking at it? These rules are how they do it. Memorize a few simple rules and simplifying fractions and prime factorization will be so much easier. Number Divisibility Rule Example Two (2) A number is divisible by two if it is even. Another ...
Class VI Chapter 3 – Playing with Numbers Maths Exercise 3.1
... Since the last digit of the number is 4, it is divisible by 2. On adding all the digits of the number, the sum obtained is 27. Since 27 is divisible by 3, the given number is also divisible by 3. As the number is divisible by both 2 and 3, it is divisible by 6. (b) 1258 Since the last digit of the n ...
... Since the last digit of the number is 4, it is divisible by 2. On adding all the digits of the number, the sum obtained is 27. Since 27 is divisible by 3, the given number is also divisible by 3. As the number is divisible by both 2 and 3, it is divisible by 6. (b) 1258 Since the last digit of the n ...
Factorization of Natural Numbers based on Quaternion Algebra
... The factorization problem has been challenging generations over the centuries. Since we still do not know if there exists a deterministic algorithm that computes a factor of a positive integer n in polynomial time, there is lot of research into the question ”Is factorization NP-complete?” And becaus ...
... The factorization problem has been challenging generations over the centuries. Since we still do not know if there exists a deterministic algorithm that computes a factor of a positive integer n in polynomial time, there is lot of research into the question ”Is factorization NP-complete?” And becaus ...