Building Equivalent Fractions, the Least Common Denominator, and
... In order to compare, add, and subtract fractions, you will most often find it necessary to build them up to equivalent fractions with the same denominator. This is because the rewrite allows you to easily compare, add, or subtract parts (the numerators) when you represent the same number of equal pa ...
... In order to compare, add, and subtract fractions, you will most often find it necessary to build them up to equivalent fractions with the same denominator. This is because the rewrite allows you to easily compare, add, or subtract parts (the numerators) when you represent the same number of equal pa ...
When Is na Sum of k Squares? - Mathematical Association of America
... r3 (n) = 3r2 (n). In three hours, a laptop search using Mathematica’s built-in SquaresR function verified that the conjectured values for S are correct for n ≤ 5 × 106 . Sums of four positive squares In [6], Pall is credited with showing that n can be written as a sum of four positive squares if and ...
... r3 (n) = 3r2 (n). In three hours, a laptop search using Mathematica’s built-in SquaresR function verified that the conjectured values for S are correct for n ≤ 5 × 106 . Sums of four positive squares In [6], Pall is credited with showing that n can be written as a sum of four positive squares if and ...
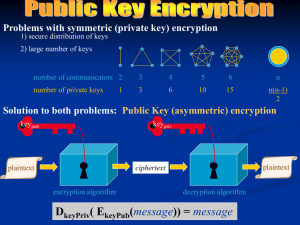
ModernCrypto2015-Session4-v7
... q is called a quadratic residue modulo n if there exists an integer x such that x2 ≡ q (mod n). Otherwise, q is called a quadratic nonresidue modulo n. Deciding whether a given number is a quadratic residue modulo n: ...
... q is called a quadratic residue modulo n if there exists an integer x such that x2 ≡ q (mod n). Otherwise, q is called a quadratic nonresidue modulo n. Deciding whether a given number is a quadratic residue modulo n: ...
WS-Prime factors - investigate
... 2) By looking at the answers to Q1, write down as many rules as you can find linking a number's prime factorisation with the number of factors it has. Test your rules on other numbers. ...
... 2) By looking at the answers to Q1, write down as many rules as you can find linking a number's prime factorisation with the number of factors it has. Test your rules on other numbers. ...
Prime number theorem
In number theory, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée-Poussin in 1896 using ideas introduced by Bernhard Riemann (in particular, the Riemann zeta function).The first such distribution found is π(N) ~ N / log(N), where π(N) is the prime-counting function and log(N) is the natural logarithm of N. This means that for large enough N, the probability that a random integer not greater than N is prime is very close to 1 / log(N). Consequently, a random integer with at most 2n digits (for large enough n) is about half as likely to be prime as a random integer with at most n digits. For example, among the positive integers of at most 1000 digits, about one in 2300 is prime (log(101000) ≈ 2302.6), whereas among positive integers of at most 2000 digits, about one in 4600 is prime (log(102000) ≈ 4605.2). In other words, the average gap between consecutive prime numbers among the first N integers is roughly log(N).