Greatest Common Factor
... How can you use the greatest common factor to find the simplest form of a fraction? SAMPLE RESPONSE: If you divide the numerator and denominator of a fraction by ________________________________________________________________________ their greatest common factor, the resulting equivalent fraction w ...
... How can you use the greatest common factor to find the simplest form of a fraction? SAMPLE RESPONSE: If you divide the numerator and denominator of a fraction by ________________________________________________________________________ their greatest common factor, the resulting equivalent fraction w ...
Pretty Primes Class Notes
... To find all the divisors of 3,529,147 by this method, we’d have to sift through √3,529,147 numbers. That’s not too far from √4,000,000 = 2,000 checks. A bit much! 3. Unique Prime Factorization The first method can be very slow. To quicken it, let’s put our engineer caps on: we’ll first break our num ...
... To find all the divisors of 3,529,147 by this method, we’d have to sift through √3,529,147 numbers. That’s not too far from √4,000,000 = 2,000 checks. A bit much! 3. Unique Prime Factorization The first method can be very slow. To quicken it, let’s put our engineer caps on: we’ll first break our num ...
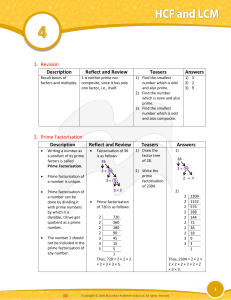
GCF
... 6.1 The Greatest Common Factors and Factoring by Grouping A. Finding the Greatest common Factor (GCF) of a List of Integers or a list of terms Greatest common Factor (GCF)—is the largest common factor of the integers in the list. Steps: 1. Write each of the numbers as a product of prim ...
... 6.1 The Greatest Common Factors and Factoring by Grouping A. Finding the Greatest common Factor (GCF) of a List of Integers or a list of terms Greatest common Factor (GCF)—is the largest common factor of the integers in the list. Steps: 1. Write each of the numbers as a product of prim ...
Prime number theorem
In number theory, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée-Poussin in 1896 using ideas introduced by Bernhard Riemann (in particular, the Riemann zeta function).The first such distribution found is π(N) ~ N / log(N), where π(N) is the prime-counting function and log(N) is the natural logarithm of N. This means that for large enough N, the probability that a random integer not greater than N is prime is very close to 1 / log(N). Consequently, a random integer with at most 2n digits (for large enough n) is about half as likely to be prime as a random integer with at most n digits. For example, among the positive integers of at most 1000 digits, about one in 2300 is prime (log(101000) ≈ 2302.6), whereas among positive integers of at most 2000 digits, about one in 4600 is prime (log(102000) ≈ 4605.2). In other words, the average gap between consecutive prime numbers among the first N integers is roughly log(N).