Download Theoretical work in the CUA. Strongly correlated many

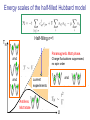
The Center for Ultracold Atoms
at MIT and Harvard
Strongly Correlated Many-Body Systems
Theoretical work in the CUA
Advisory Committee Visit, May 13-14, 2010
Role of theory in the CUA
Collaboration with experimental groups
• Stability of superfluid currents in optical lattices
Theory: Harvard. Experiment: MIT
• Dynamics of crossing the ferromagnetic Stoner transition
Theory: Harvard. Experiment: MIT
• Dynamic crossing of the superfluid to Mott transition in optical lattices
Theory: Harvard. Experiment: Harvard
Explore new systems that are not yet studied
experimentally but may be realized in the future
• Adiaibatic preparation of magnetic and d-wave paired states in lattices
Collaboration of groups by Lukin, Demler, Greiner
• Phase sensitive detection of nontrivial pairing
Collaboration of groups of Demler, Greiner
• Tonks-Girardeau gas of photons in hollow fibers
Collaboration of groups by Lukin, Demler, Vuletic
• Subwavelength resolution
Collaboration of groups by Lukin, Greiner
Connection to experimental groups all over the world
Bose-Einstein condensation of
weakly interacting atoms
Density
Typical distance between atoms
Typical scattering length
1013 cm-1
300 nm
10 nm
Scattering length is much smaller than characteristic interparticle distances.
Interactions are weak
New Era in Cold Atoms Research
Focus on Systems with Strong Interactions
• Feshbach resonances.
Scattering length comparable
to interparticle distances
• Optical lattices.
Suppressed kinetic energy.
Enhanced role of interactions
• Low dimensional systems.
Strongly interacting regimes
at low densities
Ketterle,
Zwierlein
Greiner,
Ketterle
Greiner
Theoretical work in the CUA
New challenges and new opportunities
Fermionic Hubbard model. Old model new questions
• Novel temperature regime,
• New probes, e.g. lattice modulation experiments
• Nonequilibrium phenomena
New systems
Alkali-Earth atoms. Systems with SU(N) symmetry
New questions of many-body nonequilibrium dynamics
Important for reaching equilibrium states
Convenient time scales for experimental study
Fundamental open problem
• Expansion of interacting fermions
• Photon fermionization
Fermionic Hubbard model
New questions posed by
experiments with cold atoms
Quantum simulations with ultracold atoms
Atoms in optical lattice
Antiferromagnetic and
superconducting Tc
of the order of 100 K
Antiferromagnetism and
pairing at sub-micro Kelvin
temperatures
Same microscopic model
Energy scales of the half-filled Hubbard model
Half-filling n=1
TN
Paramagnetic Mott phase.
Charge fluctuations suppressed,
no spin order
and
and
and
current
experiments
Antiferro
Mott state
U
Lattice Modulation as a probe of the Mott
state
Experiment:
• Modulate lattice intensity
• Measure number Doublons
Latest spectral data ETH
Original Experiment:
R. Joerdens et al.,
Nature 455:204 (2008)
Theory: Sensarma, Pekker,
Lukin, Demler,
PRL 103, 035303 (2009)
Temperature dependence
Psinglet
Density
Reduced probability to find a singlet on neighboring sites
Radius
Radius
D. Pekker,
L. Pollet
What can we learn from
lattice modulation experiments?
Low Temperature
• Rate of doublon production in linear response approximation
q
• Fine structure due to spinwave shake-off
• Sharp absorption edge from coherent quasiparticles
• Signature of AFM!
k-q
Open problems:
Develop theoretical approaches for connecting
high and low temperature regimes
Other modulation type experiments:
e.g. oscillation of the Optical Lattice phase
Intermediate temperature regime for spinful
bosons.
Nonequilibrium phenomena
Equilibration of different
degrees of freedom
Adiabatic preparation.
Understand time scales for preparation of
magnetically ordered states
Nonequilibrium phenomena in fermionic Hubbard model
Doublons – repulsively bound pairs
What is their lifetime?
Direct decay is
not allowed by
energy conservation
Excess energy U should be
converted to kinetic energy of single
atoms
Decay of doublon into a pair of quasiparticles
requires creation of many particle-hole pairs
Doublon decay in a compressible state
N. Strohmaier, D. Pekker, et al., PRL (2010)
Perturbation theory to order n=U/6t
Decay probability
To calculate the decay rate: consider
processes which maximize the
number of particle-hole excitations
Expt: ETHZ
Theory: Harvard
New systems that are not yet studied
experimentally but may be realized in the future
Alkali-Earth atoms. Systems with SU(N) symmetry
Two-Orbital SU(N) Magnetism with
Ultracold Alkaline-Earth Atoms
A. Gorshkov, et al., Nature Physics, in press
Ex: 87Sr (I = 9/2)
Alkaline-Earth atoms in optical lattice:
|e> = 3P0
698 nm
150 s ~ 1 mHz
|g> = 1S0
[Picture: Greiner (2002)]
Nuclear spin decoupled from electrons SU(N=2I+1) symmetry
→ SU(N) spin models ⇒ valence-bond-solid & spin-liquid phases
• orbital degree of freedom ⇒ spin-orbital physics
→ Kugel-Khomskii model [transition metal oxides with perovskite
structure]
→ SU(N) Kondo lattice model [for N=2, colossal magnetoresistance in
manganese oxides and heavy fermion materials]
Nonequilibrium many-body dynamics
Important for reaching equilibrium states
Convenient time scales for experimental study
Fundamental open problem
Expansion of interacting fermions
Expansion of interacting fermions in optical lattice
Experiment: I. Bloch et al.,
Theory: A. Rosch, E. Demler, et al.
New dynamical symmetry:
identical slowdown of expansion
for attractive and repulsive
interactions
Nonequilibrium many-body dynamics
Photon fermionization
Strongly correlated systems of photons
Nature Physics (2008)
Self-interaction effects for one-dimensional optical waves
BEFORE: two level systems and
NOW: EIT and tight
insufficient mode confinement
mode confinement
Interaction corresponds to attraction.
Physics of solitons
Weak non-linearity due to insufficient
mode confining
Limit on non-linearity due to
photon decay
Sign of the interaction can be tuned
Tight confinement of the
electromagnetic mode
enhances nonlinearity
Strong non-linearity without losses
can be achieved using EIT
Experimental detection of the Luttinger liquid of photons
Control beam off.
Coherent pulse of
non-interacting photons
enters the fiber.
c
Control beam switched on adiabatically.
Converts the pulse into a Luttinger liquid
of photons.
“Fermionization” of photons detected by observing oscillations in g2
In equilibrium in
a Luttinger liquid
K – Luttinger parameter
Non-equilibrium dynamics of strongly
correlated many-body systems
g2 for expanding Tonks-Girardeau gas
with adiabatic switching of interactions
100 photons after expansion
Universaility in dynamics of
nonlinear classical systems
Universality in quantum manybody systems in equilibrium
Solitons in nonlinear wave propagation
Broken symmetries
Bernard cells in the presence of T gradient
Fermi liquid state
Do we have universality in nonequilibrium
dynamics of many-body quantum systems?