* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 4
Survey
Document related concepts
Classical central-force problem wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Equations of motion wikipedia , lookup
Centripetal force wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Work (physics) wikipedia , lookup
Transcript
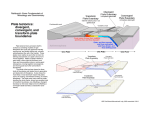
Basic concept: The outermost layer (LITHOSPHERE) is divided in a small number of “rigid” plates in relative motion one respect to the other Basic assumption: The generation of new plate material occurs by sea floor spreading. The new oceanic lithosphere form part of a rigid plate that may or may not include continental material. The Earth’s surface area remains constant; this means that seafloor spreading must be balanced by consumption of plate elsewhere. Lithospheric plates are capable of transmitting stress over great horizontal distances. In other words plates are rigid and the deformation is concentrated along the boundaries. From: Fowler, the solid Earth Lecture 6 May 24th 2005 Lecture 6 May 24th 2005 Lecture 6 May 24th 2005 Lecture 6 May 24th 2005 Lecture 6 May 24th 2005 Lecture 6 May 24th 2005 FLAT EARTH Transform LL Convergent Constructive Transform RL Lecture 6 May 24th 2005 Great Circles Eulerian Vector Eulerian Pole Small Circles Lecture 6 May 24th 2005 Eulerian Theoreme: Every finite motion on the surface of a sphere can be described as a rotation around an axis passing throught the center of the sphere. The intersection of the axis with the sphere is calledEulerian Pole. Lecture 6 May 24th 2005 On a sphere: • Plates move along small circles. I.e. the velocity is tangential to small circles and perpendicular to great circles. •Transform fault are following small circles •Constructive and convergent plate boundaries are directed as great circles Lecture 6 May 24th 2005 On a sphere: • Velocity increase while the distance from the pole of rotation increase. Lecture 6 May 24th 2005 If we know the velocity or slip direction of a plate we can find the pole as the intersection of the great circles perpendicular to the velocity vector If we know the direction of transform faults the pole is at the intersection of great circles perpendicular to the transform The pole is also at the intersection of great circles indicated by ridge segments Lecture 6 May 24th 2005 If we assume rigid plated the motion can be described by Eulerian poles. Magnetic anomalies and bathymetry give us some of the data we need to find the Eulerian pole that describe the plate motion. Since Mag. Anomalies give a time scale we can compute also the velocity. Lecture 6 May 24th 2005 Uncertainty using: Ridges and ttransform directions Slip or velocity directions From Cox and Hart Lecture 6 May 24th 2005 Seismicity and slip direction give another constrain From DeMets et al 1990 Lecture 6 May 24th 2005 From DeMets et al 1990 Velocity as distance from the pole give a constrain on the pole position From Cox and Hart Lecture 6 May 24th 2005 A good constrain for global plate is plate closure Do it by hand Lecture 6 May 24th 2005 Lecture 6 May 24th 2005 Do it by hand Lecture 6 May 24th 2005 Lecture 6 May 24th 2005 Lecture 6 May 24th 2005