Download Chapter 16

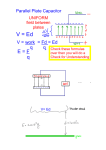
Chapter 16
Electrical Energy and
Capacitance
Electrical Potential Energy
• The electrostatic force is a conservative force
• It is possible to define an electrical potential energy
function associated with this force
• Work done by a conservative force is equal to the
negative of the change in potential energy
W = – Δ PE
Work and Potential Energy
• There is a uniform field between
the two plates
• As the charge moves from A to
B, work is done on it
W = F d = q Ex (xf – xi)
Δ PE = – W = – q Ex (xf – xi)
Potential Difference
• The potential difference between points A and B – the
change in the potential energy of a charge q moved
from A to B divided by the charge
ΔV = VB – VA = ΔPE / q
ΔPE = q ΔV
• Both electrical potential energy and
difference are scalar quantities
Alessandro Giuseppe
Antonio Anastasio
potential Volta
1745-1827
• SI unit of potential difference is Volt (V): 1 V = 1 J/C
• For a uniform electric field: ΔV
= VB – VA= – Ex Δx
Energy and Charge Movements
• A positive (negative) charge gains (loses)
electrical potential energy when it is moves
in the direction opposite the electric field
• If a charge is released in the electric field, it
experiences a force and accelerates,
gaining kinetic energy and losing an equal
amount of electrical potential energy
• When the electric field is directed
downward, point B is at a lower potential
than point A: a positive test charge moving
from A to B loses electrical potential energy
Chapter 16
Problem 6
To recharge a 12-V battery, a battery charger must move
3.6 × 105 C of charge from the negative terminal to the
positive terminal. How much work is done by the charger?
Express your answer in joules.
The Electron Volt
• The electron volt (eV) is defined as the energy
that an electron gains when accelerated through
a potential difference of 1 V: 1 eV = 1.6 x 10-19 J
Electric Potential of a Point Charge
• The point of zero electric potential is taken to be at
an infinite distance from the charge
• The potential created by a point charge q at a
distance r from the charge is
q
V  ke
r
• A potential exists at some point in space whether or
not there is a test charge at that point
Electric Potential of a Point Charge
• The electric potential is proportional to 1/r while the
electric field is proportional to 1/r2
q
V  ke
r
Electric Potential of Multiple Point
Charges
• Superposition principle applies
• The total electric potential at some point P due to
several point charges is the algebraic sum of the
electric potentials due to the individual charges
(potentials are scalar quantities)
• V1: the electric potential due to q1 at P
• The work required to bring q2 from infinity to P
without acceleration is q2V1 and it is equal to the
potential energy of the two particle system
q1q2
PE  q2V1  ke
r
Electric Potential of Multiple Point
Charges
• If the charges have the same sign, PE is positive
(positive work must be done to force the two
charges near one another), so the charges would
repel
• If the charges have opposite signs, PE is negative
(work must be done to hold back the unlike charges
from accelerating as they are brought close
together), so the force would be attractive
q1q2
PE  q2V1  ke
r
Solving Problems
with Electric Potential (Point Charges)
• Note the point of interest and draw a diagram of all
charges
• Calculate the distance from each charge to the point of
interest
• Use the basic equation V = keq/r and include the sign
– the potential is positive (negative) if the charge is
positive (negative)
• Use the superposition principle when you have
multiple charges and take the algebraic sum (potential
is a scalar quantity and there are no components to
worry about)
Chapter 16
Problem 17
The three charges in the figure are at the
vertices of an isosceles triangle. Let q = 7.00 nC,
and calculate the electric potential at the
midpoint of the base.
Potentials and Charged Conductors
• Since W = – q (VB – VA), no work is
required to move a charge between two
points that are at the same electric
potential (W
= 0 when VA = VB)
• For a charged conductor in
electrostatic equilibrium the electric
field just outside the conductor is
perpendicular to the surface
• Path AB is perpendicular to the electric
field lines at every point – the work will
be zero along AB, so all points on the
surface of are at the same potential
Potentials and Charged Conductors
• Since all of the charge resides at the
surface,
E = 0 inside the conductor
• Therefore work will be zero along any
path inside the conductor, so the
potential everywhere inside the
conductor is constant and equal to its
value at the surface
Equipotential Surfaces
• An equipotential surface is a surface
on which all points are at the same
potential
• No work is required to move a charge
at a constant speed on an
equipotential surface
• The electric field at every point on an
equipotential surface is perpendicular
to the surface
• For a point charge the equipotential
surfaces are a family of spheres
centered on the point charge
Equipotential Surfaces
• An equipotential surface is a surface
on which all points are at the same
potential
• No work is required to move a charge
at a constant speed on an
equipotential surface
• The electric field at every point on an
equipotential surface is perpendicular
to the surface
• For a dipole the equipotential surfaces
are are shown in blue
Capacitance
• The capacitance, C, is a measure of the amount of
electric charge stored (or separated) for a given electric
potential
Q
C
V
• SI unit – Farad (F): 1 F = 1 C / V
Michael Faraday
1791 – 1867
• A 1 Farad capacitance is very large – µF or pF
capacitances are more common
Capacitor
• A capacitor is a device used in a variety of electric
circuits
• Capacitance of a capacitor is the ratio of the
magnitude of the charge on either conductor (plate)
to the magnitude of the potential difference between
the conductors (plates)
• This capacitance of a device depends on the
geometric arrangement of the conductors
Parallel-Plate Capacitor
• This capacitor consists of two parallel
plates (each of area A) separated by a
distance d each carrying equal and
opposite charges
• When connected to the battery, charge is
pulled off one plate and transferred to the
other plate (the transfer stops when ΔVcap =
Δ Vbattery)
• For a parallel-plate capacitor whose plates
are separated by air:
q A A  A
C


V V Ed ( /  o )d
A
C  o
d
Chapter 16
Problem 27
A parallel-plate capacitor has an area of 5.00 cm2, and the
plates are separated by 1.00 mm with air between them.
The capacitor stores a charge of 400 pC. (a) What is the
potential difference across the plates of the capacitor? (b)
What is the magnitude of the uniform electric field in the
region between the plates?
Electric Field in a Parallel-Plate Capacitor
• The electric field between the plates is
uniform near the center and
nonuniform near the edges
• The field may be taken as constant
throughout the region between the
plates
Electric Circuits
• A circuit is a collection of objects usually containing
a source of electrical energy (such as a battery)
connected to elements that convert electrical energy
to other forms
• A circuit diagram can be used to show the path of
the real circuit
Capacitors in Parallel
• When capacitors are first connected in
parallel in the circuit, electrons are
transferred from the left plates through the
battery to the right plates, leaving the left
plates positively charged and the right
plates negatively charged
• The flow of charges ceases when the
voltage across the capacitors equals that of
the battery
• The capacitors reach their maximum charge
when the flow of charge ceases
Capacitors in Parallel
• The total charge is equal to the sum of the
charges on the capacitors: Qtotal = Q1 + Q2
• The potential differences across the
capacitors is the same and each is equal to
the voltage of the battery
• A circuit diagram for two
capacitors in parallel
Capacitors in Parallel
• The capacitors can be replaced with one capacitor with
a equivalent capacitance Ceq – the equivalent capacitor
must have exactly the same external effect on the
circuit as the original capacitors
Q  Q1  Q2
Q1  C1V
Q2  C2 V
Q  (C1  C2 )V  Ceq V
Ceq  C1  C2
Capacitors in Parallel
• For more than two capacitors in parallel:
Ceq  C1  C2  C3  ...
• The equivalent capacitance of a parallel
combination of capacitors is greater
than any of the individual capacitors
Capacitors in Series
• When a battery is connected to the
circuit, electrons are transferred
from the left plate of C1 to the right
plate of C2 through the battery
• As this negative charge
accumulates on the right plate of C2,
an equivalent amount of negative
charge is removed from the left plate
of C2, leaving it with an excess
positive charge
• All of the right plates gain charges
of –Q and all the left plates have
charges of +Q
Capacitors in Series
• An equivalent capacitor can be
found that performs the same
function as the series combination
• The potential differences add up to
the battery voltage V  V  V
Q
Q
V1 
V2 
C1
C2
Q
Q Q

V  
C1 C2 Ceq
1
2
1
1
1
 
Ceq C1 C2
Capacitors in Series
• For more than two capacitors in series:
1
1
1
1
 
  ...
Ceq C1 C2 C3
• The equivalent capacitance is always
less than any individual capacitor in the
combination
Problem-Solving Strategy
• Be careful with the choice of units
• Combine capacitors:
• When two or more unequal capacitors are connected
in series, they carry the same charge, but the potential
differences across them are not the same
• The capacitances add as reciprocals and the
equivalent capacitance is always less than the
smallest individual capacitor
Problem-Solving Strategy
• Be careful with the choice of units
• Combine capacitors:
• When two or more capacitors are connected in parallel,
the potential differences across them are the same
• The charge on each capacitor is proportional to its
capacitance
• The capacitors add directly to give the equivalent
capacitance
Problem-Solving Strategy
• Repeat the process until there is only one single
equivalent capacitor
• Redraw the circuit and continue
• To find the charge on, or the potential difference
across, one of the capacitors, start with your final
equivalent capacitor and work back through the circuit
reductions
Chapter 16
Problem 42
Find the equivalent capacitance between
points a and b in the combination of
capacitors shown in the figure
Energy Stored in a Capacitor
• Energy stored =
½ Q ΔV
• From the definition of capacitance, this can be
rewritten in different forms
2
1
1
Q
Energy  QV  CV 2 
2
2
2C
Capacitors with Dielectrics
• A dielectric is an insulating material (e.g., rubber,
plastic, etc.)
• When placed between the plates of a capacitor, it
increases the capacitance: C
• κ - dielectric constant
• The capacitance is
multiplied by the factor κ
when the dielectric
completely fills the region
between the plates
= κ Co = κ εo (A/d)
Dielectric Strength
• For any given plate separation, there is a maximum
electric field that can be produced in the dielectric
before it breaks down and begins to conduct
• This maximum electric field is called the dielectric
strength
An Atomic Description of Dielectrics
• Polarization occurs when there is a separation
between the average positions of its negative charge
and its positive charge
• In a capacitor, the dielectric becomes polarized
because it is in an electric field that exists between
the plates
An Atomic Description of Dielectrics
• The presence of the positive (negative) charge on
the dielectric effectively reduces some of the
negative (positive) charge on the metal
• This allows more charge on the plates for a given
applied voltage and the capacitance increases
Chapter 16
Problem 49
Determine (a) the capacitance and (b) the maximum
voltage that can be applied to a Teflon®-filled parallel-plate
capacitor having a plate area of 175 cm2 and an insulation
thickness of 0.040 0 mm.
Answers to Even Numbered Problems
Chapter 16:
Problem 4
− 3.20 × 10−19 C
Answers to Even Numbered Problems
Chapter 16:
Problem 16
8.09 × 10−7 J
Answers to Even Numbered Problems
Chapter 16:
Problem 24
(a) 800 V
(b) Qf = Qi / 2
Answers to Even Numbered Problems
Chapter 16:
Problem 28
1.23 kV
Answers to Even Numbered Problems
Chapter 16:
Problem 40
6.04 μF
Answers to Even Numbered Problems
Chapter 16:
Problem 44
(a) 0.150 J
(b) 268 V