* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Resilient control systems wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Dynamic range compression wikipedia , lookup
Time-to-digital converter wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Distributed control system wikipedia , lookup
Negative feedback wikipedia , lookup
Signal-flow graph wikipedia , lookup
Power electronics wikipedia , lookup
Opto-isolator wikipedia , lookup
Television standards conversion wikipedia , lookup
Power MOSFET wikipedia , lookup
Analog-to-digital converter wikipedia , lookup
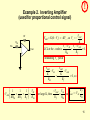
Wien bridge oscillator wikipedia , lookup
Control theory wikipedia , lookup
Integrating ADC wikipedia , lookup
PID controller wikipedia , lookup
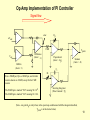
Pulse-width modulation wikipedia , lookup
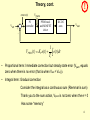
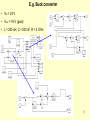
EE462L, Fall 2012 PI Voltage Controller for DC-DC Converters 1 PI Controller for DC-DC Boost Converter Output Voltage Vpwm (0-3.5V) PWM mod. and MOSFET driver DC-DC conv. Vout (0-120V) Open Loop, DC-DC Converter Process error Vset + – Hold to 90V Vpwm PI controller PWM mod. and MOSFET driver DC-DC conv. Vout (scaled down to about 1.3V) DC-DC Converter Process with Closed-Loop PI Controller 2 ! The Underlying Theory Vout ( s) G( s) Vset ( s) 1 G( s) error Vset + – Hold to 90V Vpwm PI controller PWM mod. and MOSFET driver DC-DC conv. Vout (scaled down to about 1.3V) G(s) GPI (s) GPWM (s) GDC DC (s) 1 G PI ( s ) K P sTi Proportional Integral 1 Gconv ( s) G PWM G DC DC ( s) 1 sT Our existing boost process 3 Theory, cont. error e(t) Vset + – PI controller ! Vpwm PWM mod. and MOSFET driver VPWM (t ) K P e(t ) DC-DC conv. Vout 1 e(t )dt Ti • Proportional term: Immediate correction but steady state error (Vpwm equals zero when there is no error (that is when Vset = Vout)). • Integral term: Gradual correction Consider the integral as a continuous sum (Riemman’s sum) Thank you to the sum action, Vpwm is not zero when the e = 0 Has some “memory” 4 E.g. Buck converter • Vin = 24 V • Vout = 16 V (goal) • L = 200 uH, C = 500 uF, R = 2 Ohm 5 E.g. Buck converter ! • Vin = 24 V • Vout = 16 V (goal) • L = 200 uH, C = 500 uF, R = 2 Ohm 1 VPWM (t ) e(t )dt Ti • Ki = 40, Kp = 0 iL vC d e 6 E.g. Buck converter ! • Vin = 24 V • Vout = 16 V (goal) • L = 200 uH, C = 500 uF, R = 2 Ohm 1 VPWM (t ) e(t )dt Ti • Ki = 10, Kp = 0 iL vC d e 7 E.g. Buck converter ! • Vin = 24 V • Vout = 16 V (goal) • L = 200 uH, C = 500 uF, R = 2 Ohm VPWM (t ) K P e(t ) • Ki = 0, Kp = 1 iL vC d e 8 E.g. Buck converter ! • Vin = 24 V • Vout = 16 V (goal) • L = 200 uH, C = 500 uF, R = 2 Ohm VPWM (t ) K P e(t ) • Ki = 0, Kp = 0.1 iL vC d e 9 E.g. Buck converter • Vin = 24 V • Vout = 16 V (goal) • L = 200 uH, C = 500 uF, R = 2 Ohm ! 1 VPWM (t ) K P e(t ) e(t )dt Ti • Ki = 10, Kp = 1 iL vC d e 10 Theory, cont. Ti Ri Ci 1 1 G( s) K P sTi 1 sT Response of Second Order System (zeta = 0.99, 0.8, 0.6, 0.4, 0.2, 0.1) 0.1 1.8 0.2 1.6 Vout ( s) G( s) Vset ( s) 1 G( s) 1.4 1 KP 1 s T Ti K P Vout ( s ) Vset ( s ) 1 K p 1 2 s s T TTi work! 0.8 0.6 0.2 0 0 2 Ti 0.8T 2 n K p 2 nT 1 0.99 0.4 s 2 2 n s n2 1 n2 TTi 0.4 1.2 TTi T 1 2 6 8 10 Recommended in PI literature 0.65 K p 0.45 1 K p 2T 4 T 1 Ti From above curve – gives some overshoot 11 Improperly Tuned PI Controller Mostly Integral Control - Oscillation 90V Figure 11. Closed Loop Response with Mostly Integral Control (ringing) Mostly Proportional Control – Sluggish, Steady-State Error 90V Figure 12. Closed Loop Response with Mostly Proportional Control (sluggish) 12 ! Op Amps V− I− – Vout I+ V+ + Assumptions for ideal op amp Vout = K(V+ − V− ), K large (hundreds of thousands, or one million) I+ = I− = 0 Voltages are with respect to power supply ground (not shown) Output current is not limited 13 ! Example 1. Buffer Amplifier (converts high impedance signal to low impedance signal) Vout K (V+ V− ) = K(Vin – Vout) – Vout Vin + Vout KVout KVin Vout (1 K ) KVin K Vout Vin 1 K K is large Vout Vin 14 Example 2. Inverting Amplifier (used for proportional control signal) Rf Rin Vin – Vout + ! V Vout K (0 V ) KV , so V out . K V Vin V Vout 0. KCL at the – node is Rin Rf Eliminating V yields V V out Vin out Vout K K 0 , so Rin Rf 1 1 1 Vout KRin KR f R f Rf Vout Vin Vin . For large K, then , so Vout Vin . Rin Rf Rin Rin 15 ! Example 3. Inverting Difference (used for error signal) R R Va – Vout + R Vb R V Vout K (V V ) K b V , so 2 V V V b out . 2 K V Va V Vout 0 , so KCL at the – node is R R V Vout . V Va V Vout 0 , yielding V a 2 Eliminating V yields V Va V Va K V V V Vout . , or Vout 1 K b , so Vout K out K b Vout K b a 2 2 2 2 2 2 For large K , then Vout (Va Vb ) 16 Example 4. Inverting Sum (used to sum proportional and integral control signals) Vout K (0 V ) KV , so V R Va Vb R – Vout R + ! Vout . K KCL at the – node is V Va V Vb V Vout 0 , so R R R 3V Va Vb Vout . V 3 1 Va Vb . Substituting for V yields 3 out Va Vb Vout , so Vout K K Thus, for large K , Vout (Va Vb ) 17 Example 5. Inverting Integrator (used for integral control signal) ! ~ ~ Using phasor analysis, Vout K (0 V ) , so Vin ~ Vout ~ . KCL at the − node is V K Ci Ri – Vout + ~ Vout ~ Eliminating V yields K Ri ~ Vin ~ ~ ~ ~ V Vin V Vout 0. 1 Ri jC V~out ~ jC Vout 0 . Gathering terms yields K ~ 1 Vin 1 ~ ~ 1 ~ 1 jC 1 jRi C 1 Vin For large K , the , or Vout Vout K Ri K K KRi ~ Vin ~ ~ ~ expression reduces to Vout ( jRi C ) Vin , so Vout (thus, negative integrator action). jRi C ~ For a given frequency and fixed C , increasing Ri reduces the magnitude of Vout . 18 Op Amp Implementation of PI Controller Signal flow – αVout + – Vset + error Rp – + – Proportional (Gain = −Kp) Buffers (Gain = 1) The 500kΩ pot is marked “504” meaning 50 • 10 4 . The 100kΩ pot is marked “104” meaning 10 • 10 4 . Vpwm + Difference (Gain = −1) Ri is a 500kΩ pot, Rp is a 100kΩ pot, and all other resistors shown are 100kΩ, except for the 15kΩ resistor. – 15kΩ + Summer (Gain = −1 1) Ci Ri – + Inverting Integrator (Time Constant = Ti) (Note – net gain Kp is unity when, in the open loop condition and with the integrator disabled, Vpwm is at the desired value) 19